AMS机器学习课程:Keras深度学习 - 卷积神经网络正则化
本文翻译自 AMS 机器学习 Python 教程,并有部分修改。
David John Gagne, 2019: “Deep Learning with Keras”.
David John Gagne, National Center for Atmospheric Research
本文接上一篇文章《AMS机器学习课程:Keras深度学习 - 卷积神经网络》
由于要拟合大量的权重,并且要处理的数据量有限,如果神经网络受到不适当的约束,它们很容易过度拟合数据集中的噪声。 尽管使用卷积和池化确实可以充当正则化器,但对于具有许多权重的网络,可能需要其他正则化技术。
我们将讨论两种常见的正则化技术:权重衰减 (Weight decay) 和丢弃法 (Dropout)。
权重衰减
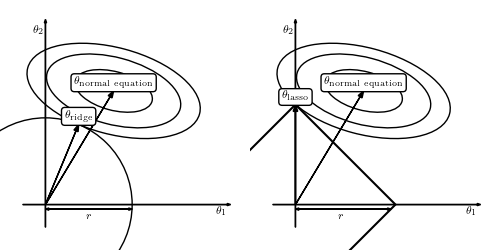
权重衰减 (Weight decay) 是一种通过在损失函数中包含惩罚项来约束回归模型权重的方法,该函数将权重的总大小最小化。 惩罚项的影响由参数 alpha 控制。
权重衰减有两种常见形式:
- Ridge (或 L2 norm,Tikhonov)
- LASSO (或 L1 norm) 正则化
Ridge 正则化将所有权重的大小减小一个恒定因子,但更相关的权重受到的影响较小,相关性较小的权重被最小化。
LASSO 正则化将不太重要的权重减小为 0,从而导致权重稀疏。 LASSO 可以用作特征选择 (feature selection) 的一种形式。
我们现在将使用权重的 Ridge 正则化训练 CNN。
这是通过在 Keras 中向每个 Conv2D 和 Dense 层添加 kernel_regularizer=l2(l2_param) 参数来完成的。
构建模型
模型参数
num_conv_filters = 8
filter_width = 5
conv_activation = "relu"
learning_rate = 0.001
l2_param = 0.001输入数据
形状:(instance, y, x, variable)
conv_net_in_l2 = Input(shape=train_norm_2d.shape[1:])
train_norm_2d.shape[1:](32, 32, 3)
第一组二维卷积层
from tensorflow.compat.v1.keras.regularizers import l2
conv_net_l2 = Conv2D(
num_conv_filters,
(filter_width, filter_width),
padding="same",
kernel_regularizer=l2(l2_param)
)(conv_net_in_l2)
conv_net_l2 = Activation(conv_activation)(conv_net_l2)平均池化采用 2x2 邻域中的平均值以减小图像大小
conv_net_l2 = AveragePooling2D()(conv_net_l2)第二组卷积层和池化层
conv_net_l2 = Conv2D(
num_conv_filters * 2,
(filter_width, filter_width),
padding="same",
kernel_regularizer=l2(l2_param)
)(conv_net_l2)
conv_net_l2 = Activation(conv_activation)(conv_net_l2)
conv_net_l2 = AveragePooling2D()(conv_net_l2)第三组卷积层和池化层
conv_net_l2 = Conv2D(
num_conv_filters * 4,
(filter_width, filter_width),
padding="same",
kernel_regularizer=l2(l2_param)
)(conv_net_l2)
conv_net_l2 = Activation(conv_activation)(conv_net_l2)
conv_net_l2 = AveragePooling2D()(conv_net_l2)将最后一个卷积层展平为长特征向量
conv_net_l2 = Flatten()(conv_net_l2)全连接输出层,相当于在最后一层做逻辑回归
conv_net_l2 = Dense(
1,
kernel_regularizer=l2(l2_param)
)(conv_net_l2)
conv_net_l2 = Activation("sigmoid")(conv_net_l2)构建模型
conv_model_l2 = Model(
conv_net_in_l2,
conv_net_l2
)使用默认的 Adam 优化器
opt = Adam(lr=learning_rate)编译模型
conv_model_l2.compile(
opt,
"binary_crossentropy"
)查看模型结构
conv_model_l2.summary()Model: "functional_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_2 (InputLayer) [(None, 32, 32, 3)] 0
_________________________________________________________________
conv2d_3 (Conv2D) (None, 32, 32, 8) 608
_________________________________________________________________
activation_4 (Activation) (None, 32, 32, 8) 0
_________________________________________________________________
average_pooling2d_3 (Average (None, 16, 16, 8) 0
_________________________________________________________________
conv2d_4 (Conv2D) (None, 16, 16, 16) 3216
_________________________________________________________________
activation_5 (Activation) (None, 16, 16, 16) 0
_________________________________________________________________
average_pooling2d_4 (Average (None, 8, 8, 16) 0
_________________________________________________________________
conv2d_5 (Conv2D) (None, 8, 8, 32) 12832
_________________________________________________________________
activation_6 (Activation) (None, 8, 8, 32) 0
_________________________________________________________________
average_pooling2d_5 (Average (None, 4, 4, 32) 0
_________________________________________________________________
flatten_1 (Flatten) (None, 512) 0
_________________________________________________________________
dense_1 (Dense) (None, 1) 513
_________________________________________________________________
activation_7 (Activation) (None, 1) 0
=================================================================
Total params: 17,169
Trainable params: 17,169
Non-trainable params: 0
_________________________________________________________________
训练模型
conv_model_l2.fit(
train_norm_2d,
train_out,
batch_size=512,
epochs=10
)Train on 76377 samples
Epoch 1/10
76377/76377 [==============================] - 23s 305us/sample - loss: 0.2160
Epoch 2/10
76377/76377 [==============================] - 23s 307us/sample - loss: 0.1574
Epoch 3/10
76377/76377 [==============================] - 24s 310us/sample - loss: 0.1413
Epoch 4/10
76377/76377 [==============================] - 23s 303us/sample - loss: 0.1306
Epoch 5/10
76377/76377 [==============================] - 23s 305us/sample - loss: 0.1234
Epoch 6/10
76377/76377 [==============================] - 23s 301us/sample - loss: 0.1196
Epoch 7/10
76377/76377 [==============================] - 23s 303us/sample - loss: 0.1167
Epoch 8/10
76377/76377 [==============================] - 25s 330us/sample - loss: 0.1137
Epoch 9/10
76377/76377 [==============================] - 24s 311us/sample - loss: 0.1132
Epoch 10/10
76377/76377 [==============================] - 23s 306us/sample - loss: 0.1102
检验
calc_verification_scores(
conv_model_l2,
test_norm_2d,
test_out
)AUC: 0.945
Brier Score: 0.031
Brier Score (Climatology): 0.050
Brier Skill Score: 0.384
丢弃法
丢弃法 (dropout) 是一种正则化技术,使人们可以在仅存储一个模型的情况下训练小型模型的任意集合。
丢弃法从原理上来讲很简单。 为 Dropout 层分配了丢弃的概率。 每次调用该层时,该层的每个输入都会根据丢弃概率随机设置为 0。 对于 0.5 的辍学率,给定神经元将被设置为 0 的可能性为50%。 对于给定的调用,大约 50% 的神经元将被设置为零,但是会有一些变化。 为了保持与完整模型相同的均值,将剩余的输入除以丢弃率。
由于某些神经元在训练过程中并不总是可用,因此丢弃法会鼓励训练过程中神经元之间的独立性。
说明
默认的丢弃过程是随机丢弃单个神经元。 对于具有空间相关数据的卷积神经网络,标准丢弃可能对结果影响不大,因此可以使用称为 SpatialDropout2D 的变体。 它不会丢弃单个神经元,而是随机丢弃整个通道。
在推断期间也可以使用丢弃来产生对预测不确定性的估计。 如果在丢弃激活的情况下多次通过网络发送同一示例,则将生成预测分布。 有证据表明此分布已得到很好的校准,但是可能需要调整丢弃率才能产生最可靠的预测间隔。
下面是一个字段中的 dropout 和 spatial dropout 的示例。
from tensorflow.compat.v1.keras.layers import (
Dropout,
SpatialDropout2D,
)
drop_in = K.placeholder((1, 10, 10, 3))
dropout_rate = 0.5
drop = Dropout(dropout_rate)(drop_in)
spatial_dropout = SpatialDropout2D(dropout_rate)(drop_in)
drop_func = K.function(
[drop_in, K.learning_phase()],
[drop, spatial_dropout]
)多次运行下面的单元格,以查看丢弃结果如何变化。
input_field = np.ones(
(1, 10, 10, 3)
)
drop_output, space_drop_output = drop_func([input_field, 1])
fig, axes = plt.subplots(
2, 3,
figsize=(12, 6)
)
axes[0, 0].set_ylabel(
"Dropout",
fontsize=14
)
axes[1, 0].set_ylabel(
"Spatial Dropout",
fontsize=14
)
for a in range(3):
axes[0, a].pcolormesh(
drop_output[0, :, :, a],
vmin=0,
vmax=2,
cmap="Reds"
)
axes[0, a].text(
5, 5,
f"Max: {drop_output[0, :, :, a].max():0.2f}\nCount: {np.count_nonzero(drop_output[0, :, :, a]):d}",
ha='center',
va='center',
fontsize=16,
color='white',
bbox=dict(facecolor='k', alpha=0.5)
)
axes[1, a].pcolormesh(
space_drop_output[0, :, :, a],
vmin=0,
vmax=2,
cmap="Reds"
)
axes[1, a].text(
5, 5,
f"Max: {space_drop_output[0, :, :, a].max():0.2f}",
ha='center',
va='center',
fontsize=16,
color='white',
bbox=dict(facecolor='k')
)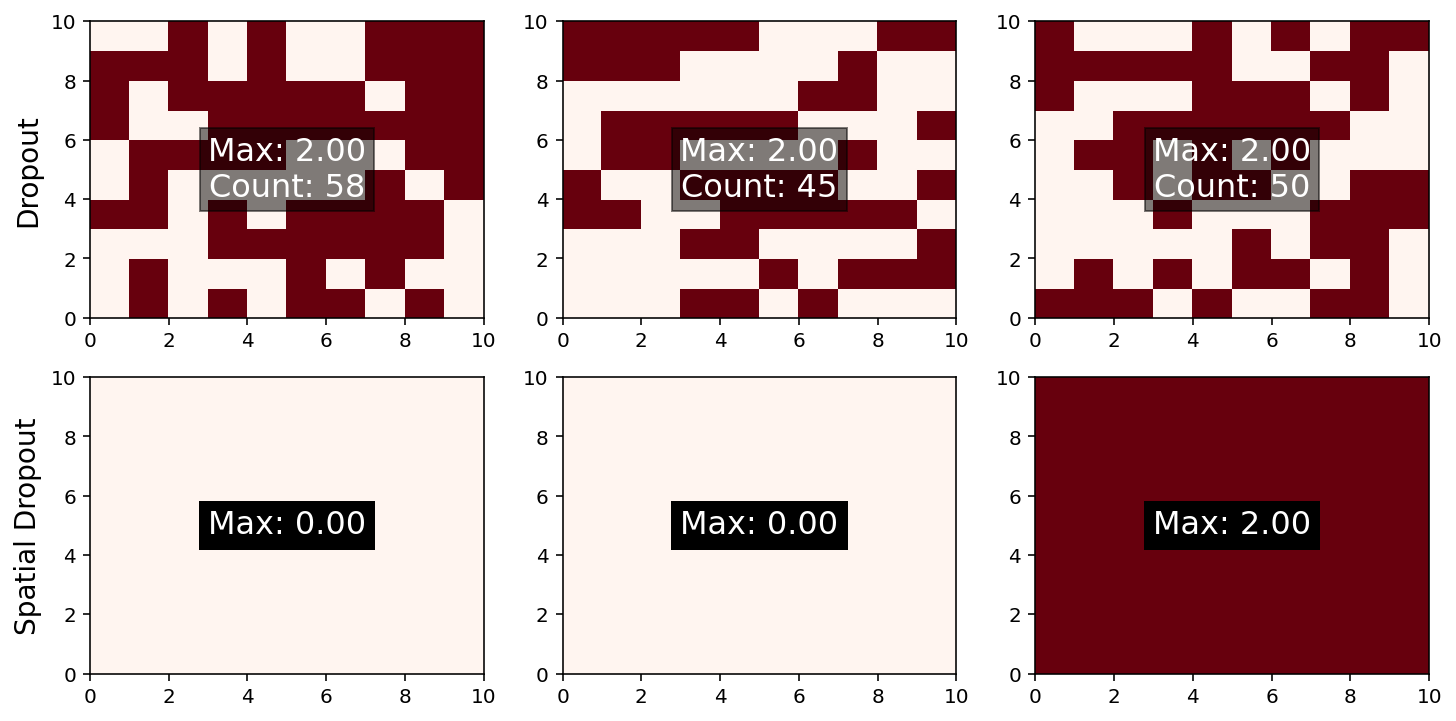
第一行使用 Dropout,可以看到每个通道中的网格数据被随机丢弃
第二行使用 SpatialDropout2D,可以看到整个通道被随机丢弃
构建模型
现在,我们将构建一个具有空间缺失层 (spatial dropout layers) 的卷积神经网络 (convolutional neural network)。
设置参数
num_conv_filters = 16
filter_width = 5
conv_activation = "relu"
learning_rate = 0.001
dropout_rate = 0.2输入数据,(instance, y, x, variable)
conv_net_in_d = Input(
shape=train_norm_2d.shape[1:]
)
train_norm_2d.shape[1:](32, 32, 3)
第一组二维卷积层
conv_net_d = Conv2D(
num_conv_filters,
(filter_width, filter_width),
padding="same"
)(conv_net_in_d)
conv_net_d = Activation(
conv_activation
)(conv_net_d)
conv_net_d = SpatialDropout2D(
dropout_rate
)(conv_net_d)平均池化层选取 2x2 区域内的平均值,以减少图像尺寸
conv_net_d = AveragePooling2D()(conv_net_d)第二组二维卷积层和池化层
conv_net_d = Conv2D(
num_conv_filters * 2,
(filter_width, filter_width),
padding="same"
)(conv_net_d)
conv_net_d = Activation(
conv_activation
)(conv_net_d)
conv_net_d = SpatialDropout2D(
dropout_rate
)(conv_net_d)
conv_net_d = AveragePooling2D()(conv_net_d)第三组二维卷积层和池化层
conv_net_d = Conv2D(
num_conv_filters * 4,
(filter_width, filter_width),
padding="same"
)(conv_net_d)
conv_net_d = Activation(
conv_activation
)(conv_net_d)
conv_net_d = SpatialDropout2D(
dropout_rate
)(conv_net_d)
conv_net_d = AveragePooling2D()(conv_net_d)将最后一个卷积层展平为长矢量
conv_net_d = Flatten()(conv_net_d)全连接输出层,相当于在最后一层做逻辑回归
conv_net_d = Dense(1)(conv_net_d)
conv_net_d = Activation("sigmoid")(conv_net_d)
conv_model_d = Model(
conv_net_in_d,
conv_net_d
)使用默认参数的 Adam 优化器
opt = Adam(lr=learning_rate)编译模型
conv_model_d.compile(
opt,
"binary_crossentropy"
)查看模型
conv_model_d.summary()Model: "functional_5"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_3 (InputLayer) [(None, 32, 32, 3)] 0
_________________________________________________________________
conv2d_6 (Conv2D) (None, 32, 32, 16) 1216
_________________________________________________________________
activation_8 (Activation) (None, 32, 32, 16) 0
_________________________________________________________________
spatial_dropout2d_1 (Spatial (None, 32, 32, 16) 0
_________________________________________________________________
average_pooling2d_6 (Average (None, 16, 16, 16) 0
_________________________________________________________________
conv2d_7 (Conv2D) (None, 16, 16, 32) 12832
_________________________________________________________________
activation_9 (Activation) (None, 16, 16, 32) 0
_________________________________________________________________
spatial_dropout2d_2 (Spatial (None, 16, 16, 32) 0
_________________________________________________________________
average_pooling2d_7 (Average (None, 8, 8, 32) 0
_________________________________________________________________
conv2d_8 (Conv2D) (None, 8, 8, 64) 51264
_________________________________________________________________
activation_10 (Activation) (None, 8, 8, 64) 0
_________________________________________________________________
spatial_dropout2d_3 (Spatial (None, 8, 8, 64) 0
_________________________________________________________________
average_pooling2d_8 (Average (None, 4, 4, 64) 0
_________________________________________________________________
flatten_2 (Flatten) (None, 1024) 0
_________________________________________________________________
dense_2 (Dense) (None, 1) 1025
_________________________________________________________________
activation_11 (Activation) (None, 1) 0
=================================================================
Total params: 66,337
Trainable params: 66,337
Non-trainable params: 0
_________________________________________________________________
训练模型
conv_model_d.fit(
train_norm_2d,
train_out,
batch_size=512,
epochs=10
)Train on 76377 samples
Epoch 1/10
76377/76377 [==============================] - 45s 592us/sample - loss: 0.1723
Epoch 2/10
76377/76377 [==============================] - 45s 594us/sample - loss: 0.1384
Epoch 3/10
76377/76377 [==============================] - 46s 599us/sample - loss: 0.1262
Epoch 4/10
76377/76377 [==============================] - 45s 592us/sample - loss: 0.1186
Epoch 5/10
76377/76377 [==============================] - 45s 589us/sample - loss: 0.1142
Epoch 6/10
76377/76377 [==============================] - 47s 614us/sample - loss: 0.1091
Epoch 7/10
76377/76377 [==============================] - 44s 573us/sample - loss: 0.1067
Epoch 8/10
76377/76377 [==============================] - 41s 530us/sample - loss: 0.1031
Epoch 9/10
76377/76377 [==============================] - 40s 522us/sample - loss: 0.1023
Epoch 10/10
76377/76377 [==============================] - 43s 562us/sample - loss: 0.1003
检验
calc_verification_scores(
conv_model_d,
test_norm_2d,
test_out
)AUC: 0.959
Brier Score: 0.029
Brier Score (Climatology): 0.050
Brier Skill Score: 0.410
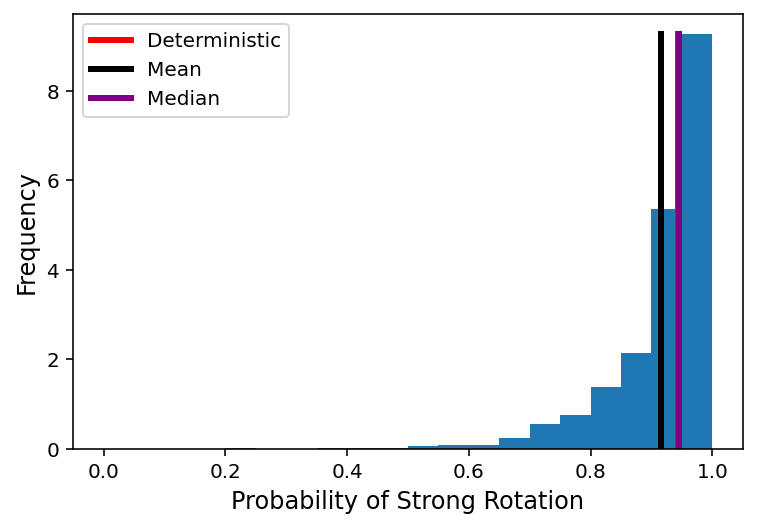
不确定度量化
最后,我们将在推断模式下使用丢弃层来生成预测分布。 不同示例的不确定性如何变化?
dist_pred = K.function(
[conv_model_d.input, K.learning_phase()],
[conv_model_d.output]
)num_samples = 1000
index = 32237
pred_values = np.zeros(num_samples)
pred_det = conv_model_d.predict(
test_norm_2d[index:index+1]
)[0, 0]
for i in range(num_samples):
pred_values[i] = dist_pred(
[test_norm_2d[index:index+1], 1]
)[0][0,0]
freqs, bins, patches = plt.hist(
pred_values,
bins=np.arange(0, 1.05, 0.05),
cumulative=False,
density=True
)
plt.plot(
[pred_det, pred_det],
[0, freqs.max()],
'r-',
lw=3,
label="Deterministic"
)
plt.plot(
[pred_values.mean(), pred_values.mean()],
[0, freqs.max()],
'k-',
lw=3,
label="Mean"
)
plt.plot(
[np.median(pred_values), np.median(pred_values)],
[0, freqs.max()],
color='purple',
lw=3,
label="Median"
)
plt.legend()
plt.xlabel(
"Probability of Strong Rotation",
fontsize=12
)
plt.ylabel(
"Frequency",
fontsize=12
)
参考
https://github.com/djgagne/ams-ml-python-course
AMS 机器学习课程
数据预处理
《数据分析与预处理》
预测雷暴旋转的基础机器学习
《数据处理》
线性回归
《线性回归》
《正则化》
《超参数试验》
逻辑回归分类
《训练》
《ROC 曲线》
《性能图》
《属性图》
《评估》
《系数与正则化》
决策树分类
《决策树》
《决策树超参数试验》
《决策树集成学习》
Keras 深度学习
《人工神经网络》
《卷积神经网络》
