数值预报模式不同时次运行时长是否相同?
数值天气预报模式业务系统每天会运行多个时次,及时向预报员提供最新的预报结果。 大部分系统不同时次之间除了输入数据外,没有显著的区别。 那么,不同时次模式积分的运行时长是否相同呢?
本文尝试使用多种方法回答这一问题。
数据
GRAPES 模式积分程序在日志中输出单步积分耗时,所有单步耗时累加可以得到模式积分总体耗时。
下面是 GRAPES MESO 3KM 模式积分程序输出的时间步长信息,使用正则表达式提取积分步数和单步积分时长。
Timing for processing for step 3901 (2021020911:44:21): 0.74780 elapsed seconds.
Timing for processing for step 3901 (2021020911:44:21): 0.74756 cpu seconds.
begin of gcr 9.699100979868703E-006
RES of gcr 9.787437371783738E-013 in 21 iterations
详细提取方法请查看如下文章:
本文使用 2020 年 8 月 1 日至 11 月 30 日 GRAPES GFS,GRAPES MESO 3KM 和 GRAPES TYM 三个业务系统的模式积分程序输出日志。 数据来自 NWPC 业务系统备份目录,少量时次的日志有缺失。
方法
使用方差分析和置换检验分析不同时次的运行时间是否相同。 使用自助法计算运行均值 95% 置信区间。 比较原始数据和重采样数据的分布。
本文所有计算和绘图结果均使用 R 语言实现,其中:
- 直方图、箱线图和频率图由 ggplot2 包绘制
- 均值与置信区间图使用 gplots 包中的
plotmeans()函数绘制 - 单因素方差分析使用
aov()函数 - 两样本/K样本置换检验使用 coin 库中的
oneway_test()函数 - 置信区间使用 boot 库计算
- Tukey HSD 检验使用
TukeyHSD()函数计算,其中一幅图形由 multcomp 包绘制
结果分析
对 GRAEPS GFS,GRAPES MESO 3KM 和 GRAPES TYM 三个模式分别进行分析。
注:以下数据时间单位均为分钟。
GRAPES GFS
GRAPES GFS 系统 00 和 12 两个时次积分 240 小时。
描述性分析
均值与标准差
| 时次 | 均值 | 标准差 |
|---|---|---|
| 00 | 38.98848 | 3.328998 |
| 12 | 38.40560 | 5.343417 |
从上述结果可以看到,两个时次的运行时长均值几乎相同,但 12 时次的标准差较大,说明 12 时次运行时长波动较大。
分布图
原始数据
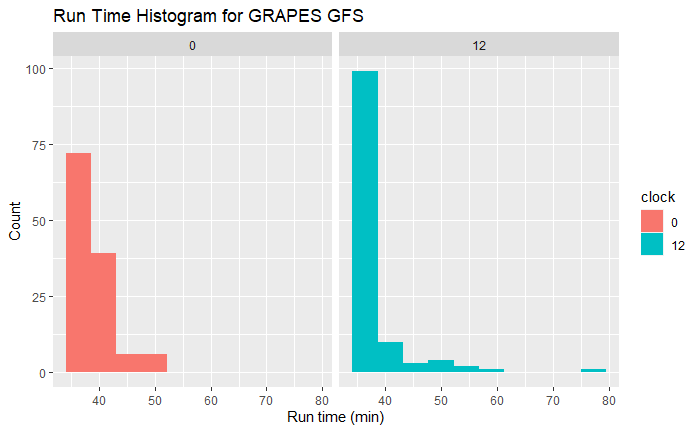
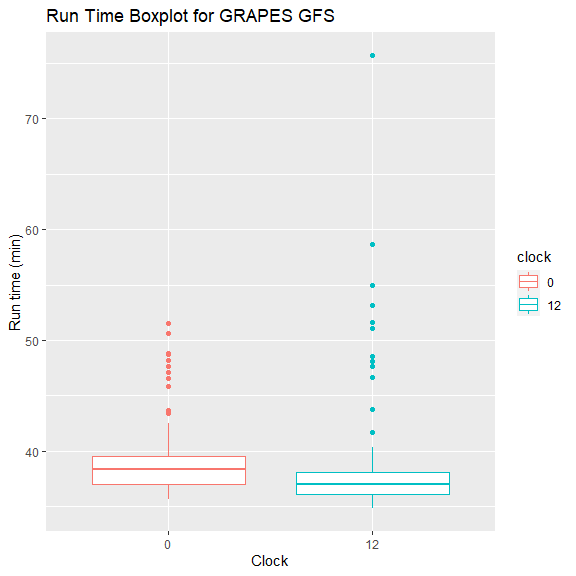
对于原始数据,12 时次运行时长偏少,但运行时长偏大的离群点比 00 时次多。
重采样数据
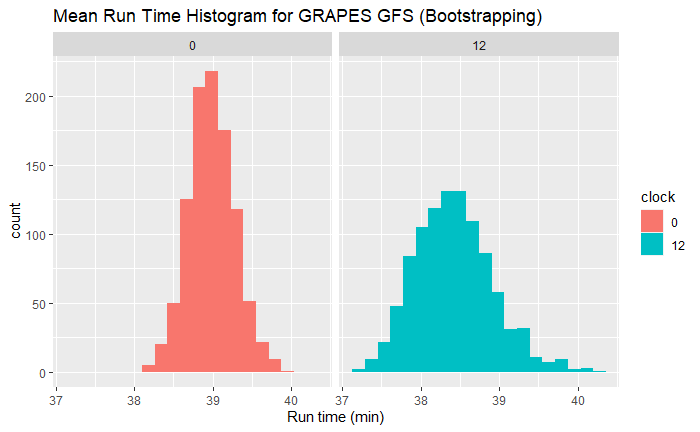
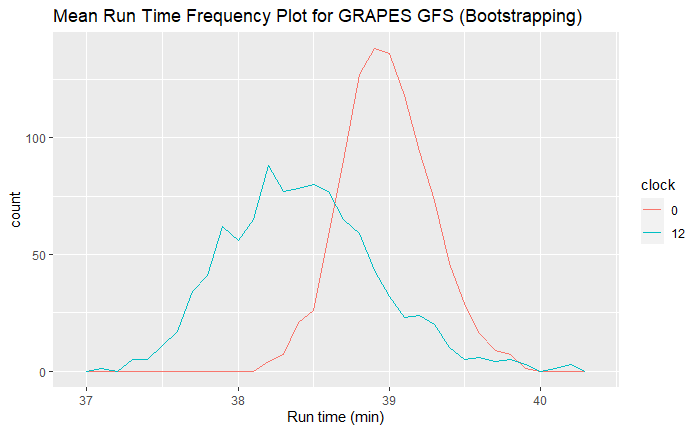
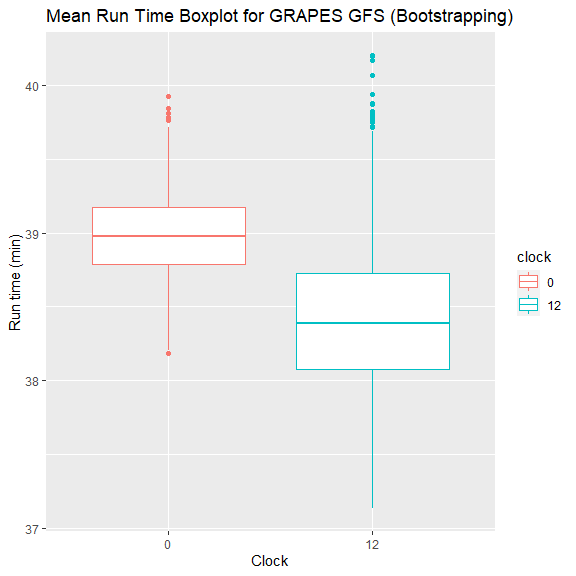
对于重采样数据,12 时次比 00 时次分布更广,但两者相差 2 分钟左右,可以忽略不计。
均值和置信区间
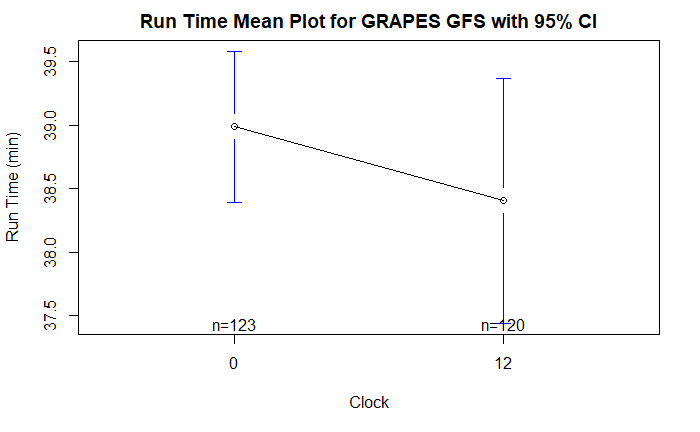
同样可以看到,GRAPES GFS 两个时次的运行时间均值相差很小。
方差分析与置换检验
对 00 和 12 两个时次进行分析
| 方法 | p 值 |
|---|---|
| 单因素方差分析 | 0.307 |
| 两样本置换检验 | 0.3115 |
两种检验结果均不显著,说明 00 和 12 两个时次运行时长没有区别。
置信区间
两个时次运行时长均值的置信区间如下:
| 时次 | 下界 | 上界 |
|---|---|---|
| 00 | 38.41753 | 39.59852 |
| 12 | 37.56889 | 39.47753 |
从均值置信区间上也可以看到,两个时次运行时长几乎相同,但 12 时次置信区间略大。
结论
从上述分析可以看到,GRAPES GFS 00 和 12 时次运行时长没有显著区别。
GRAPES MESO 3KM
GRAPES MESO 3KM 一天运行 8 次,每次积分 36 小时。
描述性分析
均值与标准差
| 时次 | 均值 | 标准差 |
|---|---|---|
| 00 | 67.78504 | 6.806254 |
| 03 | 64.75608 | 5.809834 |
| 06 | 64.51204 | 5.189582 |
| 09 | 65.87046 | 9.300791 |
| 12 | 67.97197 | 9.732788 |
| 15 | 65.33908 | 7.690270 |
| 18 | 64.06845 | 5.797037 |
| 21 | 64.63706 | 6.050846 |
从上述结果可以看到,8 个时次均值分为三类,00、12 比其余时次均值略大,09、15 属于第二梯队。 与 GRAPES GFS 相似,09、12 和 15 时次标准差较大,时长波动较大。
分布图
原始数据
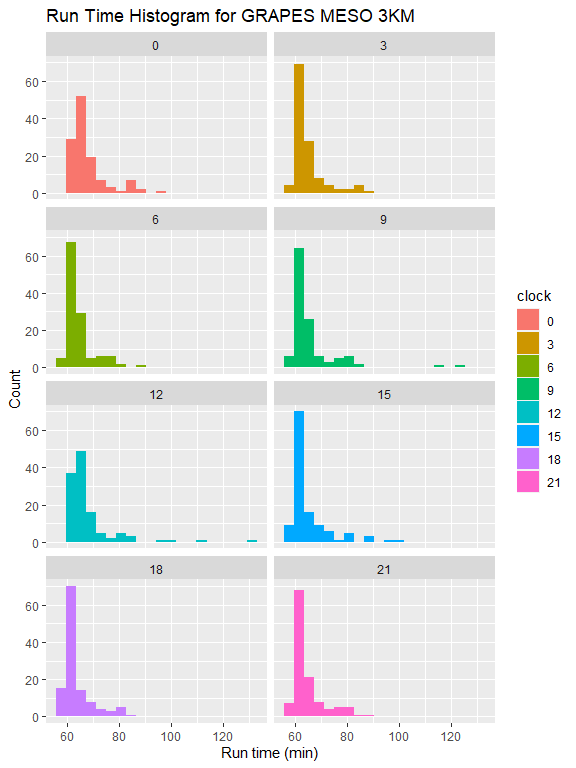
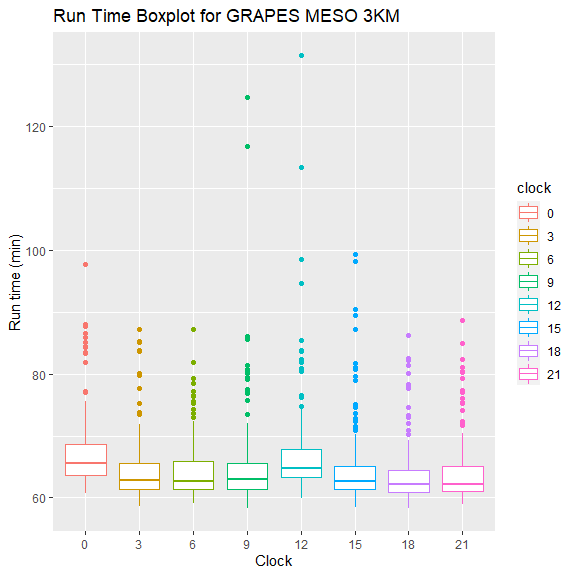
从直方图和箱线图可以看到,00、12 时次与其余时次有明显的差异,另外 09、12、15 时次运行时长偏长的离群点比较多。
重采样数据
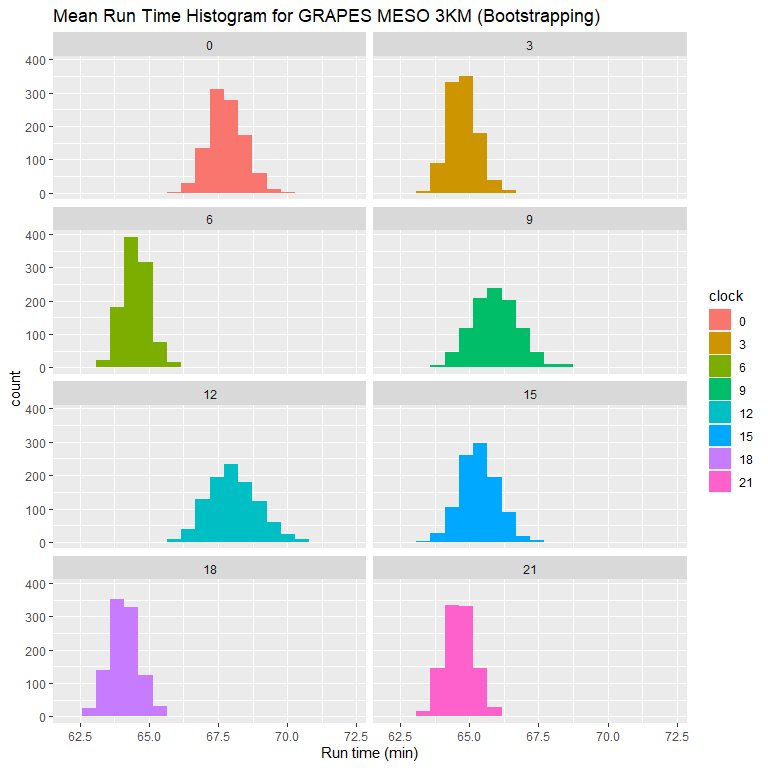
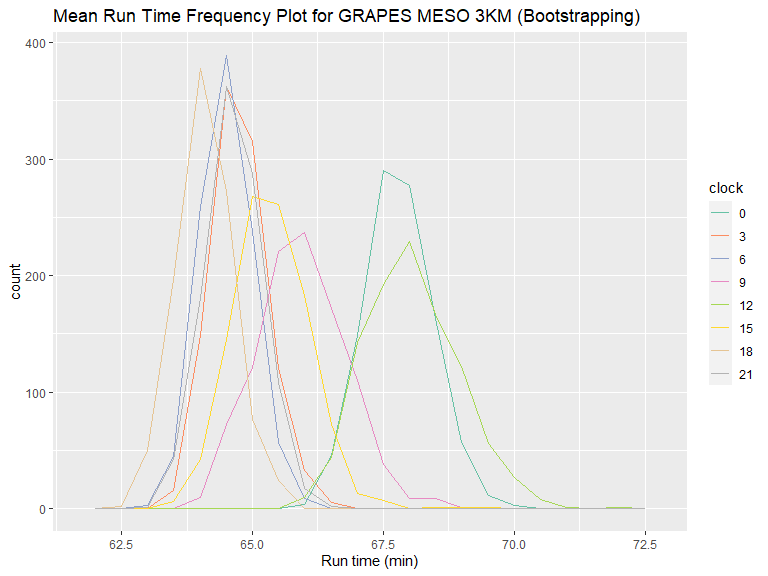
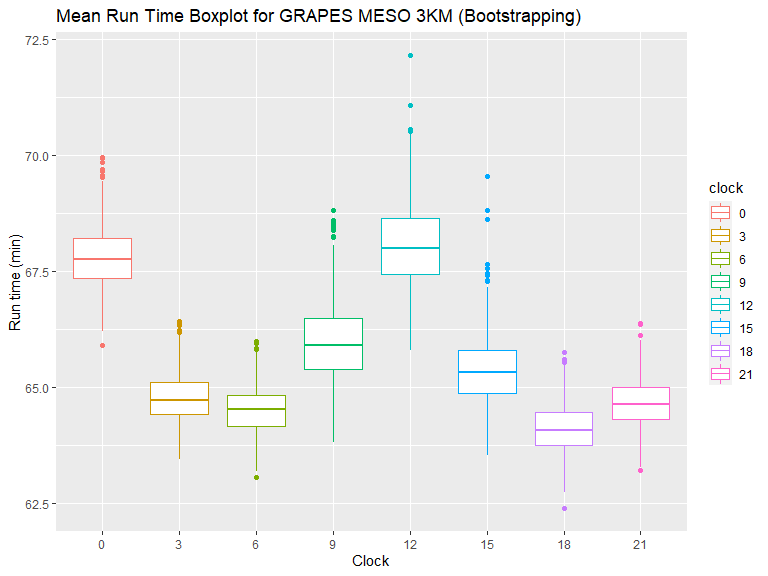
对于重采样数据,可以看到 00、12 时次均值明显大于其它时次,09、15 时次比其余 4 个时次均值略大。
均值和置信区间
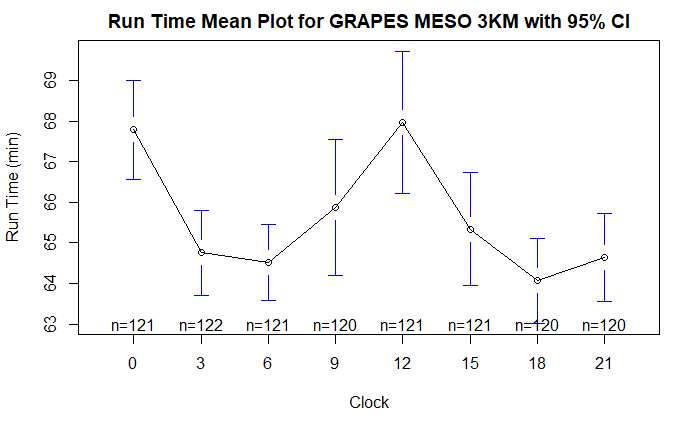
与均值和标准差的结果一致,00、12 与其它时次均值不同,09、15 时次也和其余时次有所区别。
方差分析与置换检验
对所有 8 个时次进行分析:
| 方法 | p 值 |
|---|---|
| 单因素方差分析 | 7.93e-06 |
| K 样本置换检验 | < 1e-04 |
两种检验结果均显著,说明至少一个时次运行时长与其它时次不同。
使用 Tukey HSD 检验 进行进一步分析
各个时次逐对比较,置信区间包含零说明差异不显著
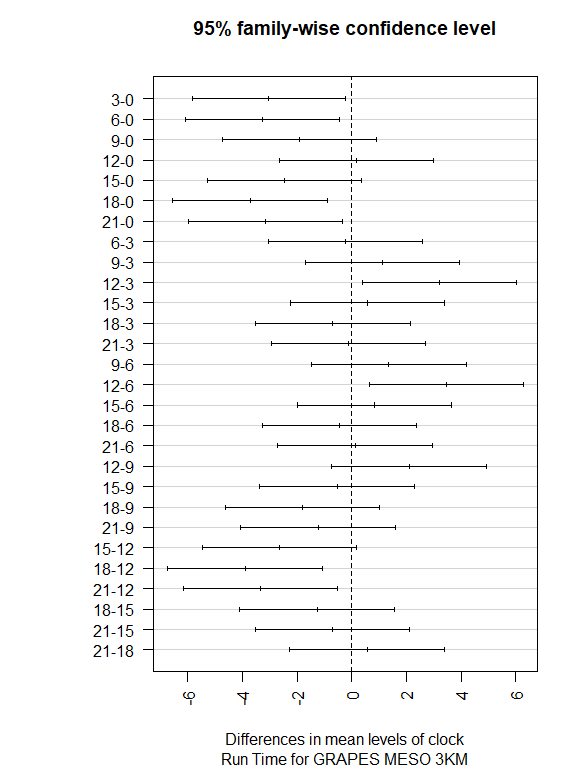
用另一种方式对比各时次间的差异,有相同字母的组说明均值差异不显著。
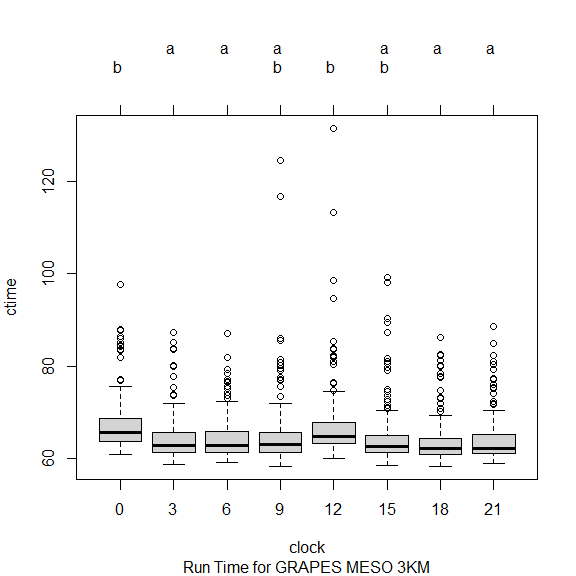
可以看到 03/06/09/15/18/21 分为一组,00/09/12/15分为一组。
置信区间
8 个时次运行时长均值的置信区间如下:
| 时次 | 下界 | 上界 |
|---|---|---|
| 00 | 66.66089 | 69.1019 |
| 03 | 63.8043 | 65.87745 |
| 06 | 63.60037 | 65.4604 |
| 09 | 64.42455 | 67.57517 |
| 12 | 66.52001 | 69.92443 |
| 15 | 64.08555 | 66.72582 |
| 18 | 63.07486 | 65.22094 |
| 21 | 63.6408 | 65.70772 |
从均值置信区间上也可以看到,00、12 时次运行时长较长,09、15 时次紧随其后,这 4 个时次的置信区间比其余 4 个时次略大。
结论
从上述分析可以看到,GRAPES MESO 3KM 运行时长不完全相同,其中 00、12 时次明显大于其余时次,09、15 时次也与其余 4 个时次不同。
因为 MESO 3KM 的 00、12 时次是冷启动,其余时次是暖启动,运行时长偏长可能与此相关。 而 09、15 时次偏长可能与 GFS 12 时次波动较大类似,不是因模式本身导致的。
GRAPES TYM
GRAPES TYM 一天运行 4 次,每次积分 120 小时。
描述性分析
均值与标准差
| 时次 | 均值 | 标准差 |
|---|---|---|
| 00 | 62.89386 | 7.302026 |
| 06 | 58.78670 | 5.485594 |
| 12 | 62.93463 | 11.107283 |
| 18 | 58.58110 | 3.177714 |
从上述结果可以看到,四个时次均值明显分为两类,00、12 时次比 06、18 时次均值略大。 与 GRAPES GFS 相似,12 时次标准差最大,时长波动最大。
分布图
原始数据
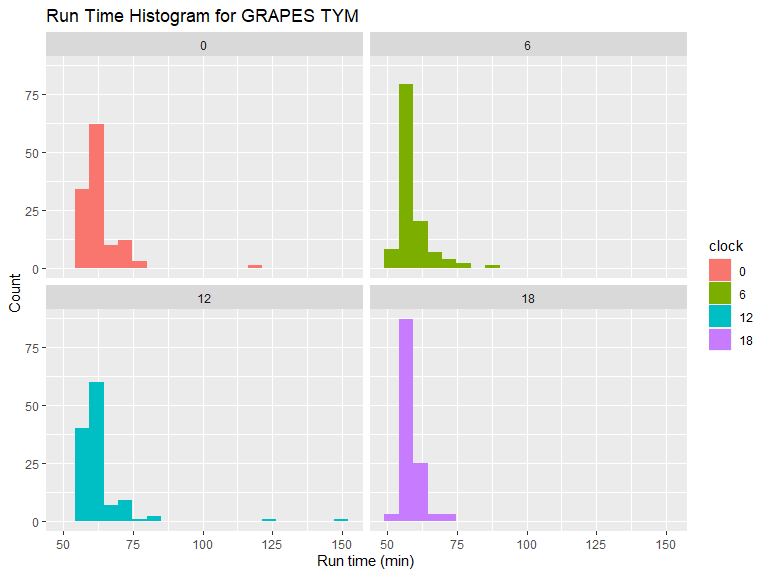
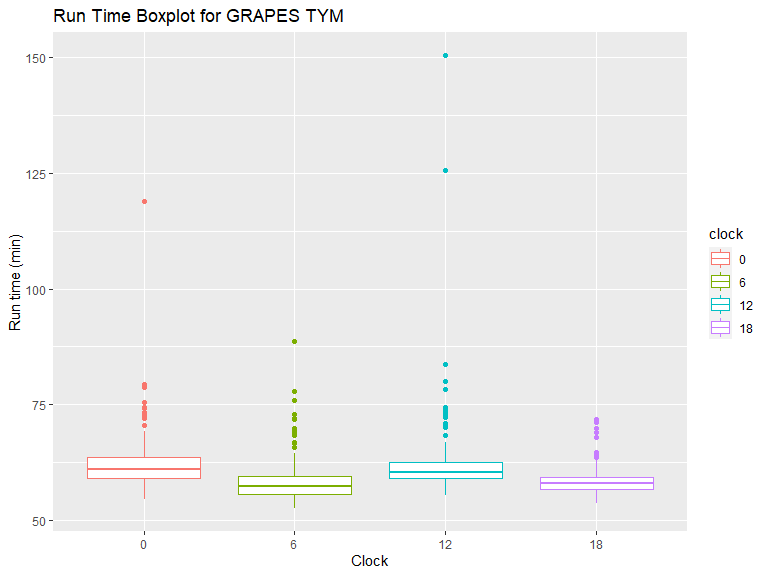
从直方图和箱线图可以看到,00、12 时次与 06、18 时次有明显的差异,12 时次运行时长偏长的离群点比较多。
重采样数据

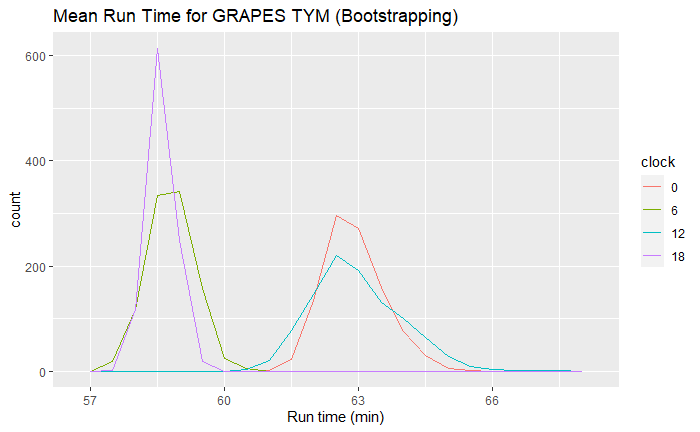
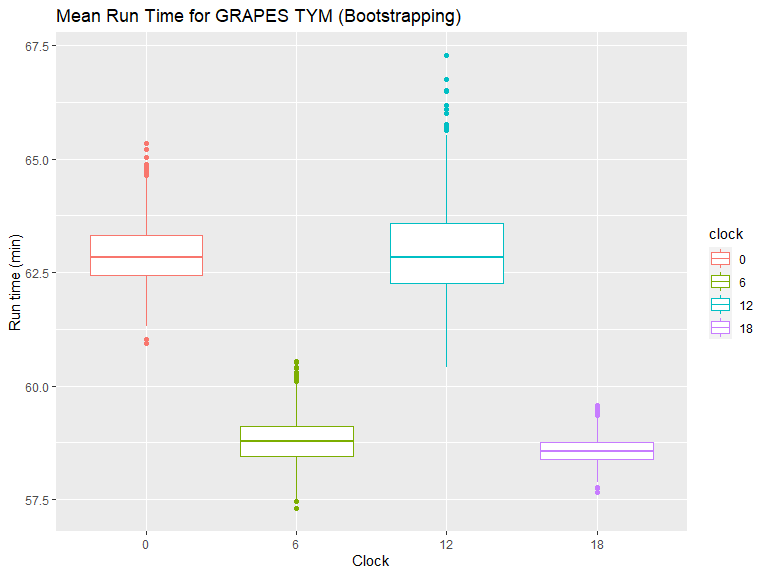
对于重采样数据,可以看到 00、12 时次均值明显大于其它时次,12 时次离群点较多。
均值和置信区间
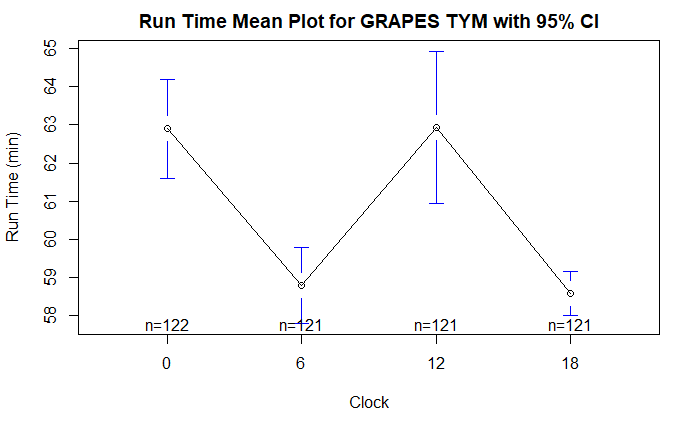
与均值和标准差的结果一致,00、12 时次与 06、18 时次均值不同, 12 时次置信区间最大。
方差分析与置换检验
对所有 4 个时次进行分析:
| 方法 | p 值 |
|---|---|
| 单因素方差分析 | 2.19e-08 |
| K 样本置换检验 | < 1e-04 |
两种检验结果均显著,说明至少一个时次运行时长与其它时次不同。
使用 Tukey HSD 检验 进行进一步分析
各个时次逐对比较,置信区间包含零说明差异不显著。
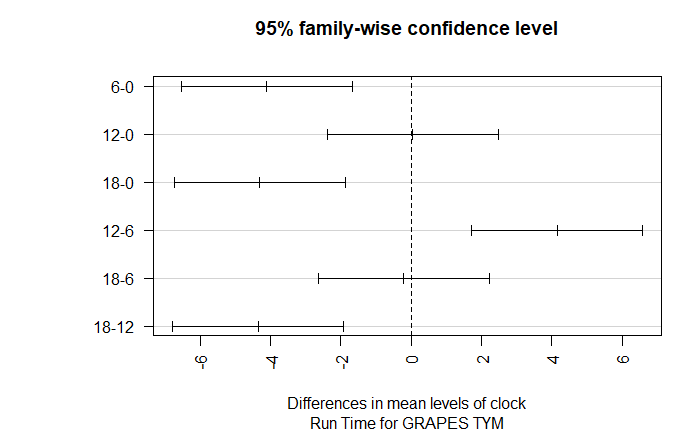
用另一种方式对比各时次间的差异,有相同字母的组说明均值差异不显著。
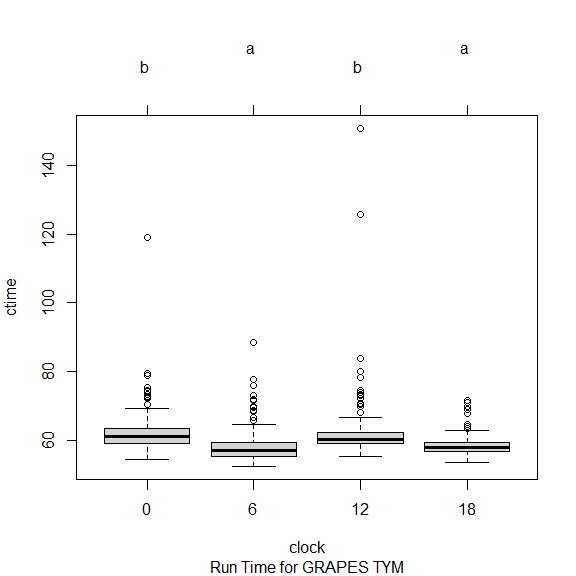
同样可以看到 00、12 与 06、18 组内没有差异但组间有区别。
置信区间
4 个时次运行时长均值的置信区间如下:
| 时次 | 下界 | 上界 |
|---|---|---|
| 00 | 61.75944 | 64.40769 |
| 06 | 57.82995 | 59.83561 |
| 12 | 61.26244 | 65.03094 |
| 18 | 58.06538 | 59.1961 |
从均值置信区间上也可以看到,00、12 时次运行时长较长,12 时次的置信区间最大。
结论
从上述分析可以看到,GRAPES TYM 运行时长不完全相同,其中 00、12 时次明显大于其余时次,12 时次运行时长波动最大。
总结
本文对 GRAPES GFS,GRAPES MESO 3KM 和 GRAPES TYM 三个业务系统的模式积分时长进行分析,得出以下结论:
- GRAPES GFS 模式 00、12 两个时次运行时长没有区别;
- GRAPES MESO 3KM 模式和 GRAPES TYM 模式的 00、12 两个时次运行时长偏长;
- 凌晨附近时次(包括各系统的 12 时次和 MESO 3KM 的 09、15 时次)运行时长的波动比较大,具体原因有待进一步研究。
笔者仅为统计学的初学者,得到的分析结果可能不够准确,后续会继续研究。
参考
模式积分日志介绍
R 语言分析方法介绍
