Dask教程:数组
本文翻译自 dask-tutorial 项目
Dask 数组使用阻塞算法提供并行,大于内存,N维的数组。 简单地说:分布式 Numpy。

- 并行 (Parallel):使用计算机的所有核
- 大于内存 (Larger-than-memory):通过将数组分解成许多小块,按顺序对这些块进行操作以最大限度地减少计算的内存占用,并有效地从磁盘流式传输数据,让您可以处理大于可用内存的数据集
- 分块算法 (Blocked Algorithms):通过执行许多较小的计算来执行大型计算
在本笔记本中,我们将通过从头开始实现一些分块算法来建立一些理解。 然后,我们将使用 Dask Array 并行分析大型数据集,使用熟悉的类似 NumPy 的 API。
相关文档
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format='retina'
创建数据
%run prep.py -d random
设置
from dask.distributed import Client
client = Client(n_workers=8)
client
分块算法
Blocked Algorithms
分块算法 通过将大型数据集分解为许多小块来在大型数据集上执行。
例如,考虑取十亿个数字的总和。 我们可以将数组分成 1,000 个块,每个块的大小为 1,000,000,取每个块的总和,然后取中间总和的总和。
我们通过执行许多较小的结果 (每个一百万个数字的一千个总和,然后是另一个一千个数字的总和) 来实现预期的结果 (一个十亿个数字的总和)。
在以下示例中,我们使用 Python 和 NumPy 完全做到这一点:
使用 h5py 加载数据,将创建数据的指针,但不实际加载数据
import h5py
from pathlib import Path
f = h5py.File(Path("data", "random.hdf5"), mode="r")
dset = f["/x"]
使用分块算法计算总和
在使用 dask 之前,让我们考虑一下分块算法的概念。 我们可以通过逐块加载它们并保持 running sum 来计算大量元素的总和。
这里我们通过下面步骤计算磁盘上这个大数组的总和:
- 计算数组的每个 1,000,000 大小块的总和
- 计算 1,000 个中间和的总和
请注意,下面代码笔记本内核中的一个顺序过程,包括加载和求和。
%%time
# 计算大数组的总和,一次一百万个数字
sums = []
for i in range(0, 1_000_000_000, 1_000_000):
chunk = dset[i: i + 1_000_000] # 拉出 numpy 数组
sums.append(chunk.sum())
total = sum(sums)
print(total)
999980528.625
Wall time: 28.5 s
练习:使用分块算法计算均值
现在我们已经看到了上面的简单示例,尝试做一个稍微复杂一点的问题。 计算数组的平均值,假设我们暂时不知道数据中有多少元素。 您可以通过使用以下步骤更改上面的代码来做到这一点:
- 计算每个块的总和
- 计算每个块的长度
- 计算 1,000 个中间和的总和和 1,000 个中间长度的总和,然后除以另一个
这种方法对于我们的案例来说有点矫枉过正,但如果我们事先不知道数组或单个块的大小,则可以很好地扩展。
# 计算数组均值
sums = []
lens = []
for i in range(0, 1_000_000_000, 1_000_000):
chunk = dset[i: i + 1_000_000] # 拉出 numpy 数组
lens.append(len(chunk))
sums.append(chunk.sum())
total = sum(sums)
length = sum(lens)
mean = total/length
print(mean)
0.999980528625
dask.array 包含这些算法
Dask.array 是一个类似 NumPy 的库,它使用这些技巧来对不适合内存的大型数据集进行操作。 它超越上面讨论的线性问题,扩展到完整的 N 维算法和 NumPy 接口的一个不错的子集。
创建 dask.array 对象
你可以使用 da.from_array 函数创建 dask.array.Array 对象。
该函数接受:
data:任何支持 NumPy 切片的对象,例如dsetchunks:告诉我们如何分组数组的块大小,例如(1_000_000,)
import dask.array as da
x = da.from_array(dset, chunks=(1_000_000,))
x

像处理 numpy 数组一样操作 dask.array 对象
现在我们有了一个数组,我们可以执行标准的 numpy 风格的计算,比如算术、数学、切片、归约等。
接口是相似的,但实际工作却有所不同。
dask_array.sum() 与 numpy_array.sum() 不做同样的事情。
区别是什么?
dask_array.sum() 创建计算的表达式。
它还没有进行计算。
numpy_array.sum() 立即计算总和。
为什么有区别?
Dask 数组被分成块。 每个块都必须显式地在该块上运行计算。 如果所需的答案来自整个数据集的一小部分,则在所有数据上运行计算将浪费 CPU 和内存。
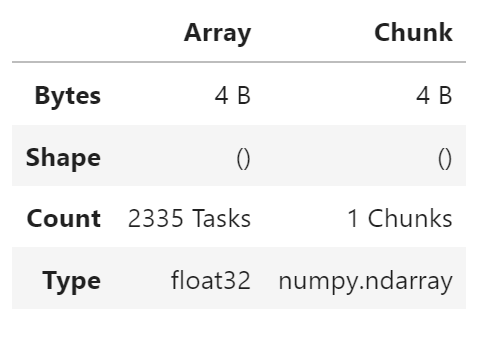
result = x.sum()
result
计算结果
Dask.array 对象延迟评估。
.sum 之类的操作构建了一个要执行的分块任务图。
我们通过调用 .compute() 来请求最终结果。这会触发实际的计算。
result.compute()
999980540.0
练习:计算均值
以及方差、标准差等。这应该是对上面示例的一个小改动。
你可以用 Jupyter notebook 的 tab-completion 查看可以做哪些其他操作。
result = x.mean()
result.compute()
0.99998057
这与您之前的结果相符吗?
性能和并行性
在我们的第一个示例中,我们使用 for 循环一次一个块地遍历数组。
对于像 sum 这样的简单操作,这是最佳的。
然而,对于复杂的操作,我们可能希望以不同的方式遍历数组。
特别是我们可能需要以下内容:
- 并行使用多个内核
- 在移动到下一个块之前对单个块进行链式操作
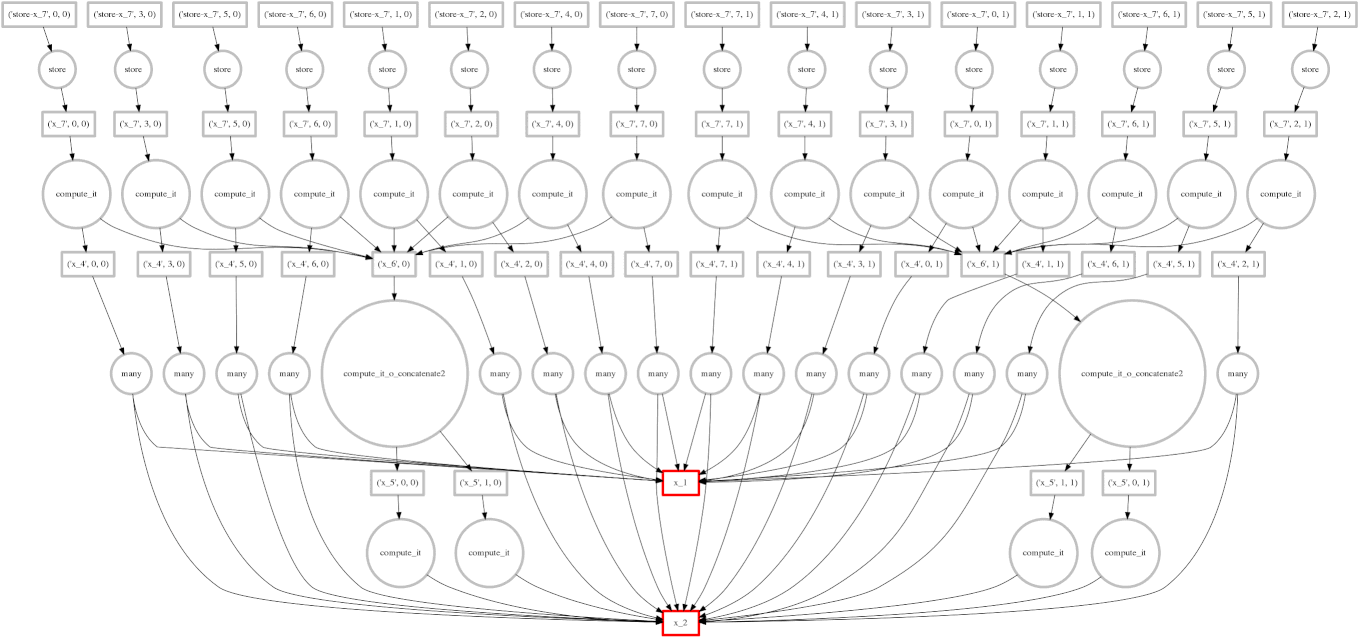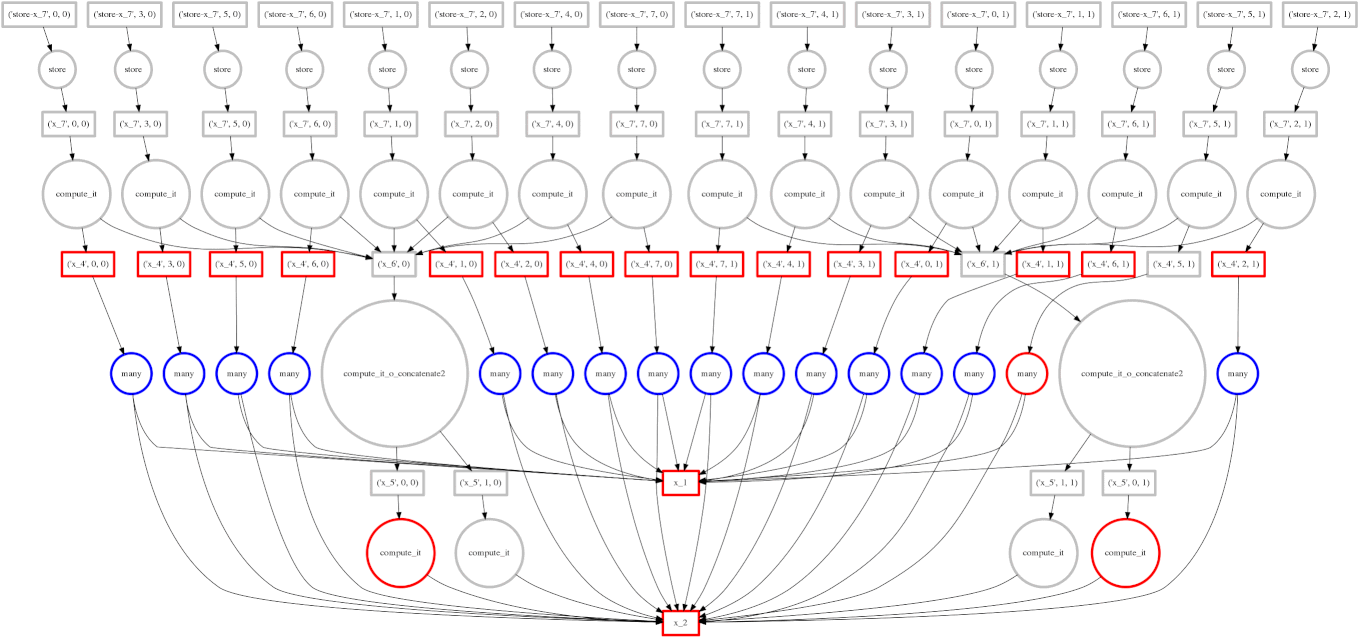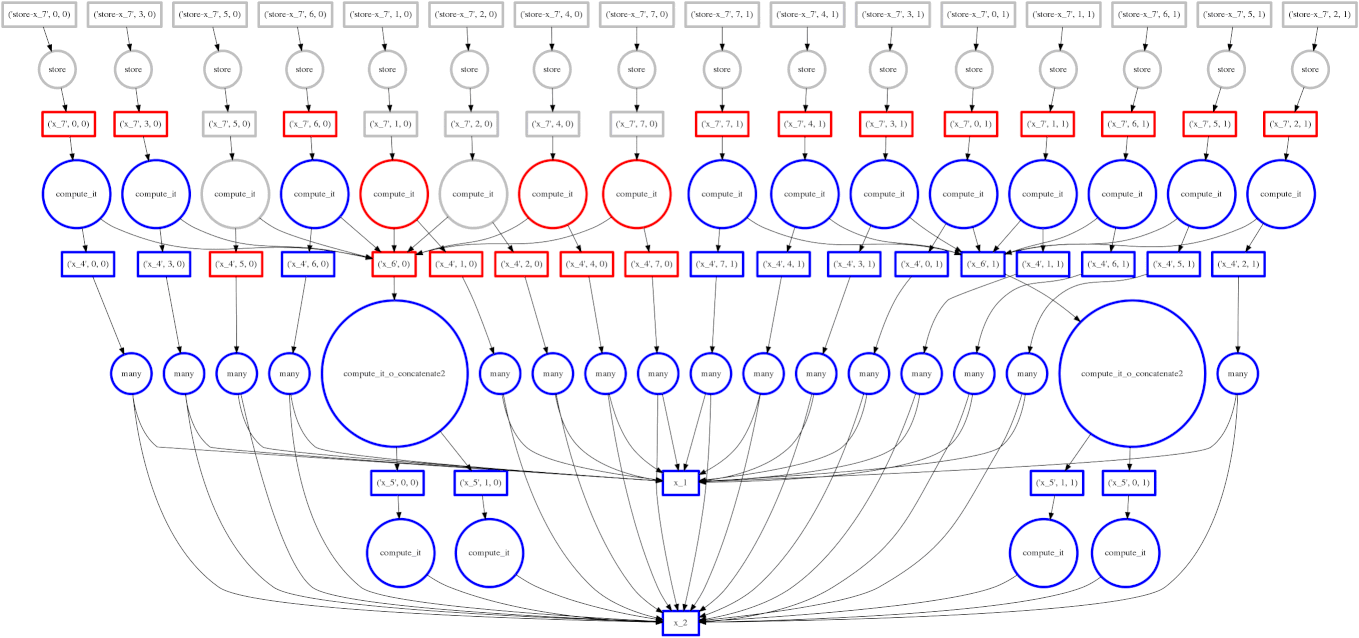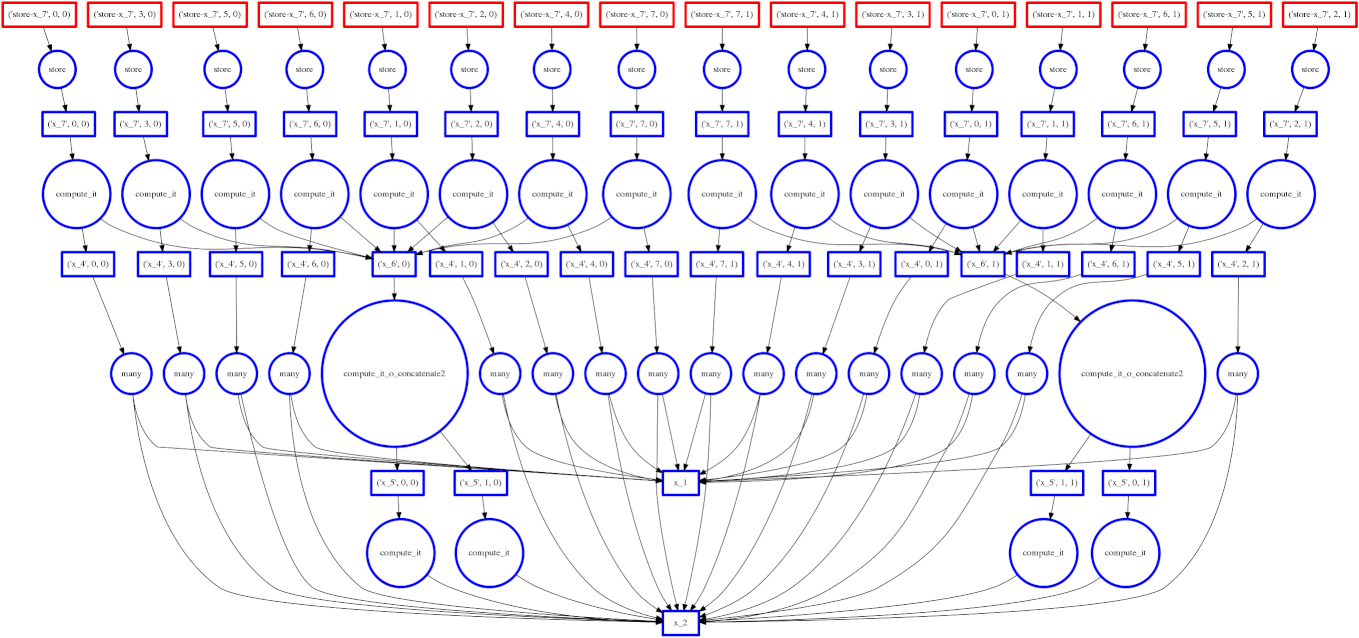
Dask.array 将您的数组操作转换为相互关联的任务图,它们之间具有数据依赖关系。
然后 Dask 使用多个线程并行执行此图。
我们将在下一节中详细讨论这一点。
示例
- 构建一个 20000x20000 的正态分布随机值数组,该数组被分成 1000x1000 大小的块
- 沿一个轴取平均值
- 每 100 个元素取一个值
import numpy as np
import dask.array as da
x = da.random.normal(
10, 0.1,
size=(20_000, 20_000), # 4亿个元素数组
chunks=(1_000, 1_000) # 切成 1000x1000 大小的块
)
y = x.mean(axis=0)[::100] # 执行 NumPy 风格的操作
延迟处理输入的 GB 字节数
x.nbytes / 1e9
3.2
计算结果的时间
%%time
y.compute()
Wall time: 3.69 s
array([ 9.9983555 , 9.99995829, 9.99950296, 9.99986182, 9.99982619,
...
10.00020971, 9.99867086, 10.00015668, 10.00062269, 9.99945275])
性能比较
以下实验是在笔者电脑上进行的。 您的表现可能会有所不同。 如果您尝试使用 NumPy 版本,请确保您拥有超过 4GB 的主内存。
NumPy
import numpy as np
%%time
x = np.random.normal(10, 0.1, size=(20000, 20000))
y = x.mean(axis=0)[::100]
y
Wall time: 11.6 s
array([10.00080417, 9.9999597 , 10.00110176, 9.9996947 , 10.0015106 ,
...
9.99995008, 9.99979497, 9.99997799, 10.00009926, 10.00007763])
Dask Array
import dask.array as da
%%time
x = da.random.normal(
10, 0.1,
size=(20000, 20000),
chunks=(1000, 1000)
)
y = x.mean(axis=0)[::100]
y.compute()
Wall time: 3.57 s
array([10.00021221, 10.00003971, 9.99979332, 10.0003238 , 10.0005408 ,
...
9.99963974, 9.99982947, 9.99990702, 10.00023817, 9.99974663])
讨论
翻译原文,因 Windows 下计时不提供用户和 CPU 时间
请注意,Dask 数组计算运行了 4 秒,但使用了 29.4 秒的用户 CPU 时间。 numpy 计算运行了 19.7 秒,并使用了 19.6 秒的用户 CPU 时间。
Dask 完成得更快,但使用了更多的总 CPU 时间,因为 Dask 能够因为块大小而透明地并行化计算。
问题
- 如果 dask chunks=(20000,20000) 会发生什么?
- 计算会在 4 秒内运行吗?
- 将使用多少内存?
- 如果 dask chunks=(25,25) 会发生什么?
- CPU和内存会发生什么?
练习:气象数据
在 data/weather-big/*.hdf5 的 HDF5 文件中有 2GB 有点儿人为的天气数据。
我们将使用 h5py 库与数据进行交互,并使用 dask.array 计算。
我们的目标是可视化该月的平均地表气温。 这需要对所有数据求平均。 我们使用下面步骤实现:
- 为磁盘上数据 (
dsets) 每天创建一个h5py.Dataset对象 - 使用
da.from_array调用包装这些对象 - 使用
da.stack在时间维度上堆叠数据集 - 使用
.method()方法沿新堆叠成的时间维度计算均值 - 使用
matplotlib.pyplot.imshow可视化结果
准备数据
%run prep.py -d weather
import h5py
from pathlib import Path
filenames = sorted(Path("data", "weather-big").glob("*.hdf5"))
dsets = [h5py.File(filename, mode="r")["/t2m"] for filename in filenames]
dsets[0]
<HDF5 dataset "t2m": shape (5760, 11520), type "<f8">
切片 h5py.Dataset 对象给出一个 numpy 数组
dsets[0][::5, ::5]
array([[22.53240967, 29.3604126 , 36.18841553, ..., 41.65081787,
...
44.03045654, 35.39703369]])
%matplotlib inline
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(16, 8))
plt.imshow(dsets[0][::4, ::4], cmap="RdBu_r")
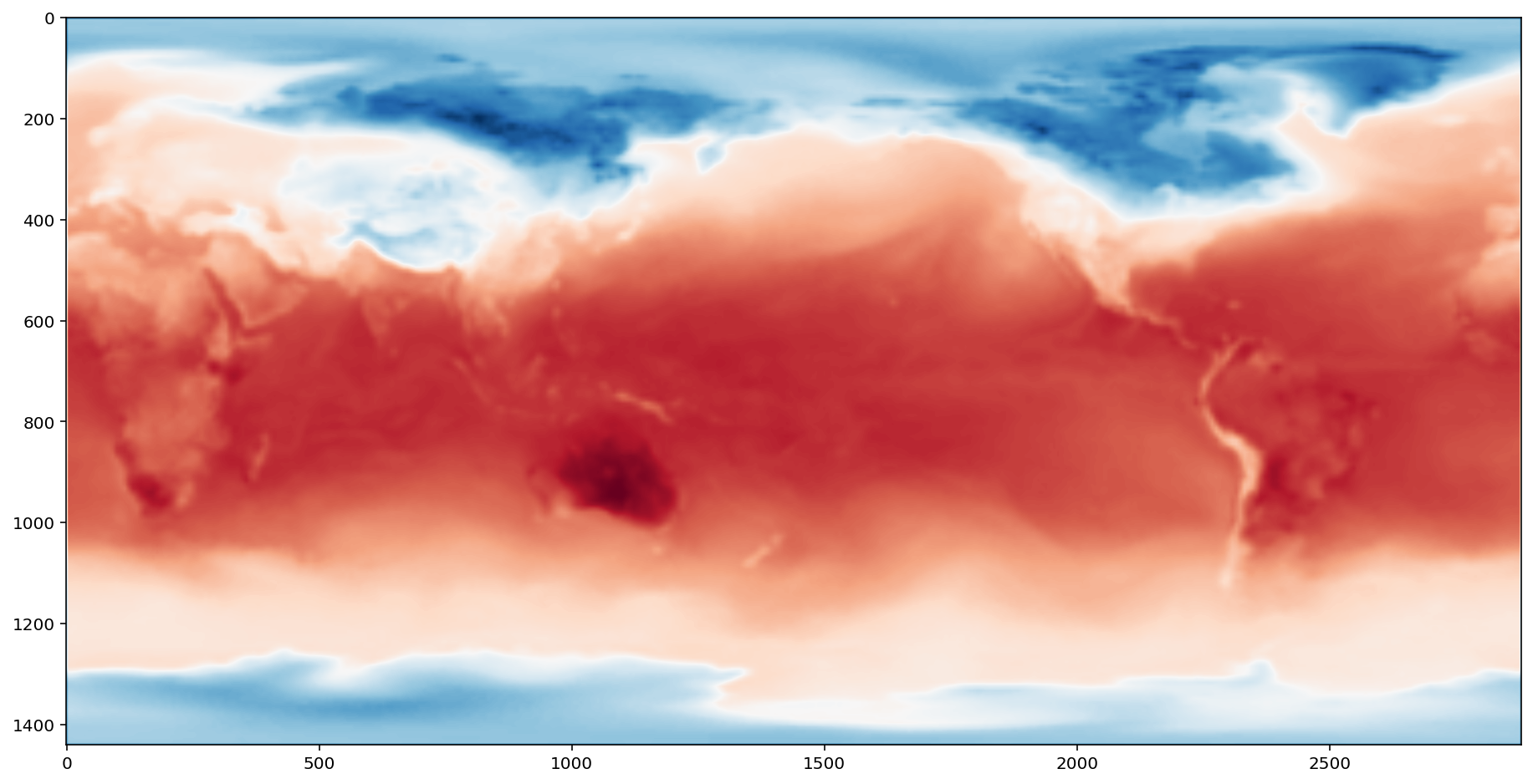
与 dask.array 集成
使用块大小为 (500, 500) 的 da.from_array 函数从 h5py.Dataset 对象列表中创建一个 dask.array 对象列表。
arrays = [da.from_array(d, chunks=(500, 500)) for d in dsets]
arrays[:2]
[dask.array<array, shape=(5760, 11520), dtype=float64, chunksize=(500, 500), chunktype=numpy.ndarray>,
dask.array<array, shape=(5760, 11520), dtype=float64, chunksize=(500, 500), chunktype=numpy.ndarray>]
arrays[0]
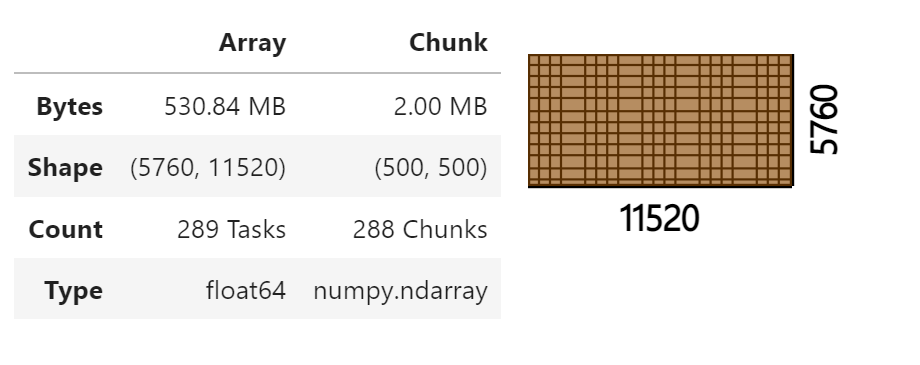
使用 da.stack 堆叠 dask.array 对象列表到单一的 dask.array 对象
沿第一个轴堆叠列表,使结果数组的形状为 (31, 5760, 11520)。
x = da.stack(arrays, axis=0)
x

沿时间轴 (0th) 绘制此数组的平均值
result = x.mean(axis=0)
fig = plt.figure(figsize=(16, 8))
plt.imshow(result, cmap="RdBu_r")
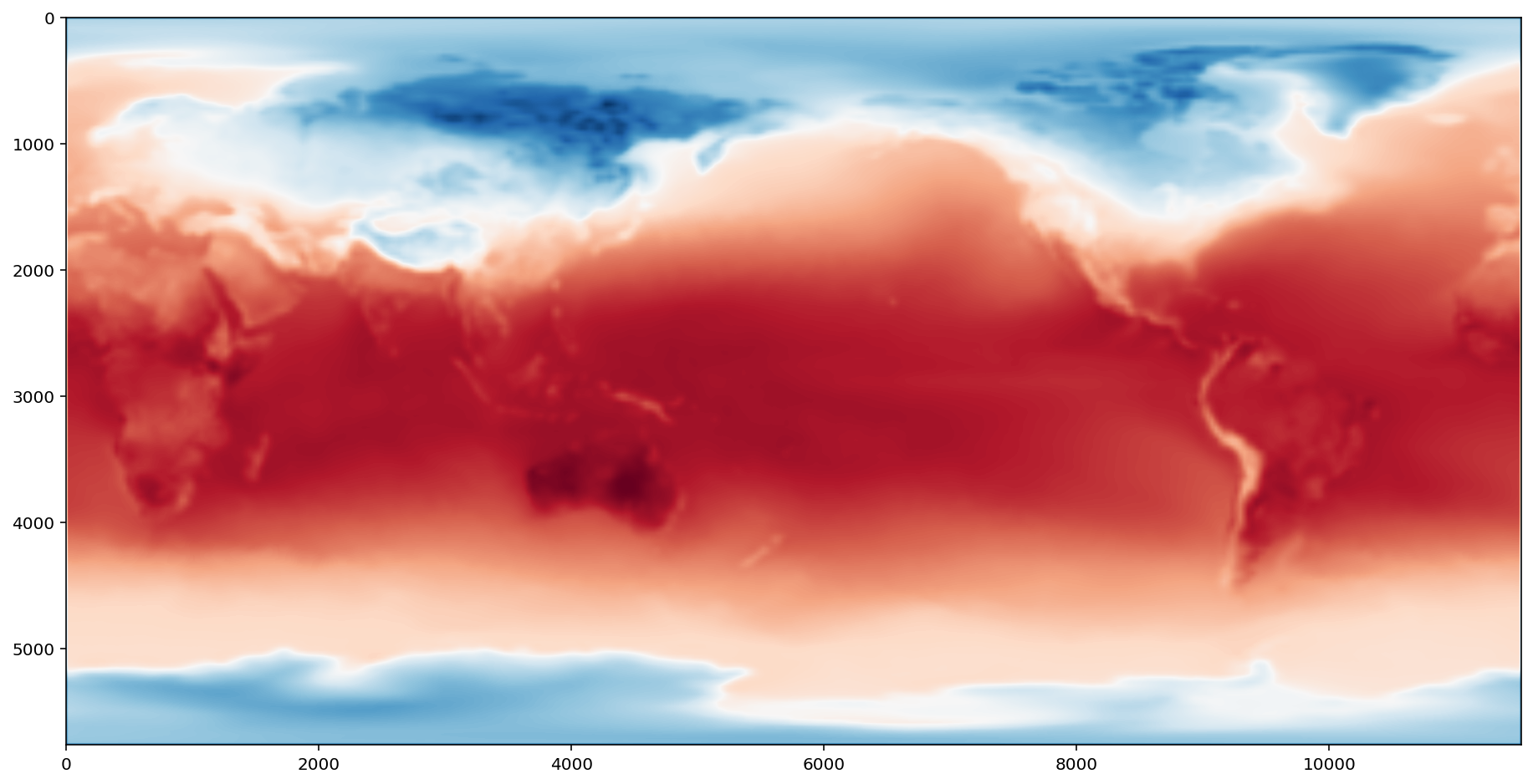
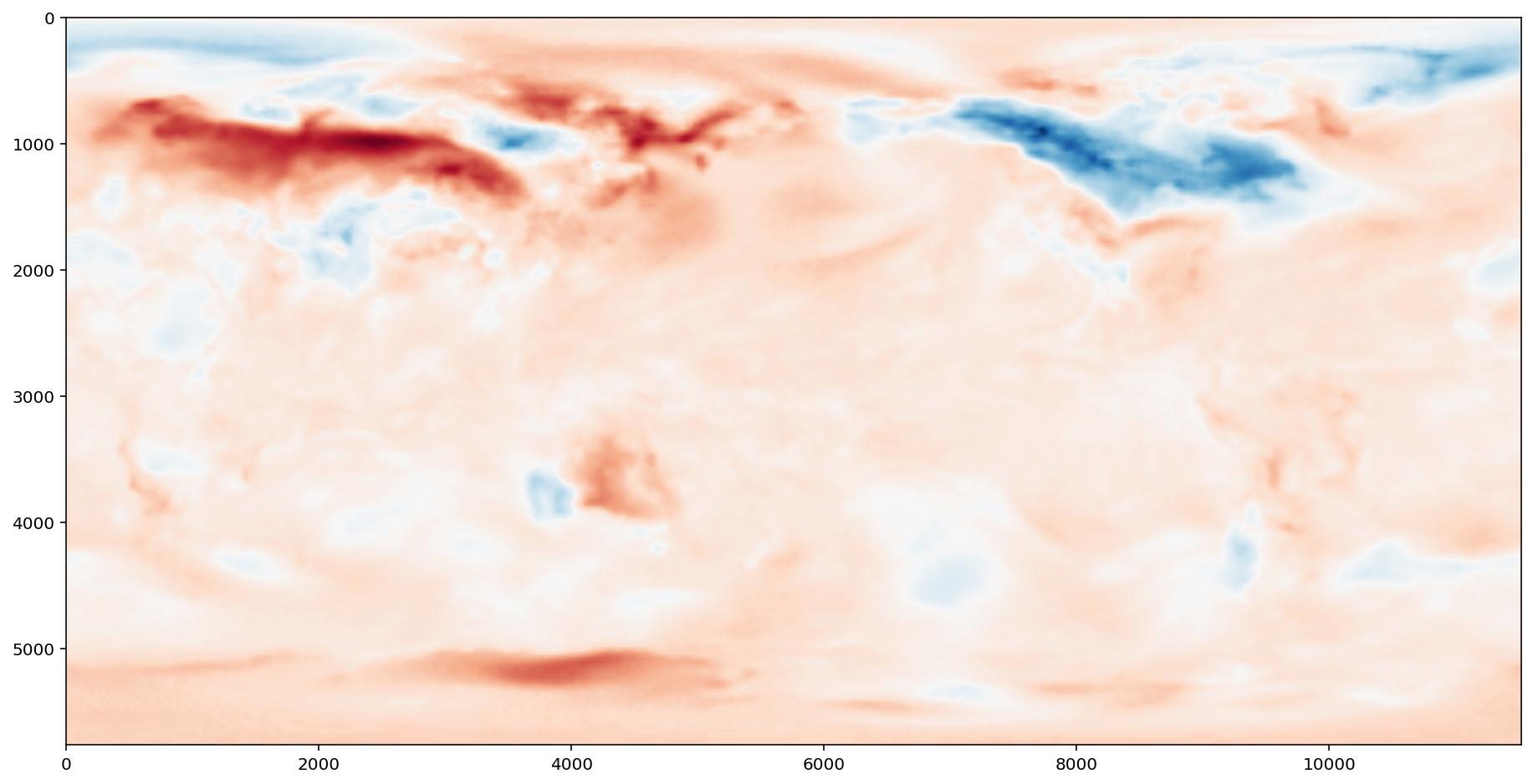
绘制第一天与平均值的差值
result = x[0] - x.mean(axis=0)
fig = plt.figure(figsize=(16, 8))
plt.imshow(result, cmap="RdBu_r")
练习:采样和存储
在上面的练习中,我们的计算结果很小,所以我们可以安全地调用 compute。 有时我们的结果仍然太大而无法放入内存,我们想将其保存到磁盘。 在这些情况下,您可以使用以下两个函数之一:
da.store:将dask.array存储到任何支持 numpy setitem 语法的对象中,例如
f = h5py.File("myfile.hdf5")
output = f.create_dataset(shape=..., dtype=...)
da.store(my_dask_array, output)
da.to_hdf5:一个专门的函数,用于将一个dask.array对象创建并存储到HDF5文件中。
da.to_hdf5("data/myfile.hdf5", "/output", my_dask_array)
本练习中的任务是使用 numpy 步进切片 (step slicing) 在纬度和经度方向以因子 2 对完整数据集进行二次采样,然后使用上面列出的函数之一将此结果存储到磁盘。
提醒一下,Python 切片需要三个元素
start:stop:step
>>> L = [1, 2, 3, 4, 5, 6, 7]
>>> L[::3]
[1, 4, 7]
import h5py
from pathlib import Path
import os
import dask.array as da
filenames = sorted(Path("data", "weather-big").glob("*.hdf5"))
dsets = [
h5py.File(filename, mode="r")["/t2m"]
for filename in filenames
]
arrays = [
da.from_array(dset, chunks=(500, 500))
for dset in dsets
]
x = da.stack(arrays, axis=0)
result = x[:, ::2, ::2]
da.to_zarr(
result,
os.path.join('data', 'myfile.zarr'),
overwrite=True
)
练习:Lennard-Jones potential
Lennard-Jones 势 用于物理、化学和工程中的粒子模拟。它是高度可并行化的。
首先,我们将在 7,000 个粒子上运行和分析 Numpy 版本。
import numpy as np
# 创建粒子随机集合
def make_cluster(notoms, radius=40, seed=1981):
np.random.seed(seed)
cluster = np.random.normal(0, radius, (notoms, 3)) - 0.5
return cluster
def lj(r2):
sr6 = (1./r2)**3
pot = 4.*(sr6*sr6 - sr6)
return pot
# 创建距离矩阵
def distances(cluster):
diff = cluster[:, np.newaxis, :] - cluster[np.newaxis, :, :]
mat = (diff*diff).sum(-1)
return mat
# 在移除接近零的距离后,在上三角形上计算 lj 函数
def potential(cluster):
d2 = distances(cluster)
dtri = np.triu(d2)
energy = lj(dtri[dtri > 1e-6]).sum()
return energy
cluster = make_cluster(int(7e3), radius=500)
%time potential(cluster)
Wall time: 4.08 s
-0.21282893668845293
请注意,最耗时的函数是 distances:
%prun -s tottime potential(cluster)
35 function calls (34 primitive calls) in 3.956 seconds
Ordered by: internal time
ncalls tottime percall cumtime percall filename:lineno(function)
1 1.316 1.316 2.082 2.082 <ipython-input-33-b553f5fe9fb4>:15(distances)
1 1.238 1.238 1.238 1.238 <ipython-input-33-b553f5fe9fb4>:9(lj)
2 0.798 0.399 0.798 0.399 {method 'reduce' of 'numpy.ufunc' objects}
1 0.309 0.309 3.875 3.875 <ipython-input-33-b553f5fe9fb4>:21(potential)
2/1 0.143 0.072 0.214 0.214 {built-in method numpy.core._multiarray_umath.implement_array_function}
1 0.080 0.080 3.956 3.956 <string>:1(<module>)
1 0.070 0.070 0.070 0.070 {method 'outer' of 'numpy.ufunc' objects}
1 0.000 0.000 3.956 3.956 {built-in method builtins.exec}
2 0.000 0.000 0.000 0.000 {built-in method numpy.arange}
1 0.000 0.000 0.070 0.070 twodim_base.py:365(tri)
1 0.000 0.000 0.210 0.210 twodim_base.py:470(triu)
2 0.000 0.000 0.798 0.399 {method 'sum' of 'numpy.ndarray' objects}
1 0.000 0.000 0.214 0.214 <__array_function__ internals>:2(triu)
2 0.000 0.000 0.798 0.399 _methods.py:45(_sum)
1 0.000 0.000 0.000 0.000 {method 'astype' of 'numpy.ndarray' objects}
1 0.000 0.000 0.000 0.000 {built-in method numpy.zeros}
1 0.000 0.000 0.140 0.140 <__array_function__ internals>:2(where)
2 0.000 0.000 0.000 0.000 twodim_base.py:31(_min_int)
4 0.000 0.000 0.000 0.000 getlimits.py:538(max)
1 0.000 0.000 0.000 0.000 _asarray.py:110(asanyarray)
2 0.000 0.000 0.000 0.000 getlimits.py:525(min)
1 0.000 0.000 0.000 0.000 {built-in method numpy.array}
1 0.000 0.000 0.000 0.000 multiarray.py:321(where)
1 0.000 0.000 0.000 0.000 twodim_base.py:427(_trilu_dispatcher)
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
绘图版本
%load_ext snakeviz
%snakeviz potential(cluster)
Dask 版本
这是 Dask 版本。只需要重写 potential 函数以最好地利用 Dask。
请注意,da.nansum 已用于整个 $NxN$ 距离矩阵以提高并行效率。
import dask.array as da
# 计算整个距离矩阵的 potential 并忽略除以零
def potential_dask(cluster):
d2 = distances(cluster)
energy = da.nansum(lj(d2))/2.
return energy
让我们将 NumPy 数组转换为 Dask 数组。 由于整个 NumPy 数组适合内存,因此按 CPU 内核数对数组进行分块在计算上更有效。
from os import cpu_count
dcluster = da.from_array(
cluster,
chunks=cluster.shape[0]//cpu_count()
)
这一步应该可以很好地扩展到内核数。
警告抱怨除以零,这就是我们在 potential_dask 中使用 da.nansum 的原因。
e = potential_dask(dcluster)
%time e.compute()
Wall time: 1.93 s
-0.21282893668845304
限制
Dask Array 没有实现整个 numpy 接口。 期待这一点的用户会感到失望。 值得注意的是 Dask Array 有以下缺点:
- Dask 并没有实现所有的
np.linalg。这已经由许多优秀的 BLAS/LAPACK 实现完成,并且是众多正在进行的学术研究项目的重点。 - Dask Array 不支持某些结果形状取决于数组值的操作。对于它确实支持的那些(例如,用另一个布尔掩码屏蔽一个 Dask 数组),块大小将是未知的,这可能会导致其他需要知道块大小的操作出现问题。
- Dask Array 不会尝试像
sort这样的操作,这些操作众所周知难以并行执行,并且在非常大的数据上价值会有所降低(您实际上很少需要完整排序)。通常我们会包含并行友好的替代方案,如topk。 - Dask 开发是由迫在眉睫的需求驱动的,因此许多不太常用的功能,如
np.sometrue并不是纯粹出于懒惰而实现的。这些将做出出色的社区贡献。
client.shutdown()
参考
Dask 教程
