ISLR习题:线性回归 - 共线性问题
目录
本文源自《统计学习导论:基于R语言应用》(ISLR) 第三章习题
创建一组有共线性关系的数据集
set.seed(1)
x1 <- runif(100)
x2 <- 0.5 + x1 + rnorm(100) / 10
y <- 2 + 2 * x1 + 0.3 * x2 + rnorm(100)
y=2+2x1+0.3x2
相关性
cor(x1, x2)
[1] 0.9469723
plot(x1, x2)
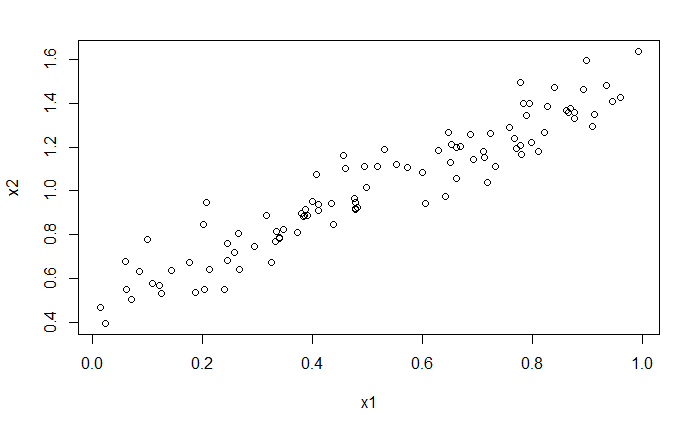
拟合
lm_fit_v1 <- lm(y ~ x1 + x2)
summary(lm_fit_v1)
Call:
lm(formula = y ~ x1 + x2)
Residuals:
Min 1Q Median 3Q Max
-2.8311 -0.7273 -0.0537 0.6338 2.3359
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.7757 0.5933 2.993 0.00351 **
x1 1.0847 1.2346 0.879 0.38179
x2 1.0097 1.1337 0.891 0.37536
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.056 on 97 degrees of freedom
Multiple R-squared: 0.2333, Adjusted R-squared: 0.2175
F-statistic: 14.76 on 2 and 97 DF, p-value: 2.54e-06
预测的 beta_1 和 beta_2 与真实值相差过大
x1 和 x2 系数的 p 值过小,不能拒绝零假设
单变量拟合
y 对 x1
lm_fit_x1 <- lm(y ~ x1)
summary(lm_fit_x1)
Call:
lm(formula = y ~ x1)
Residuals:
Min 1Q Median 3Q Max
-2.89495 -0.66874 -0.07785 0.59221 2.45560
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.2624 0.2307 9.805 3.21e-16 ***
x1 2.1259 0.3963 5.365 5.42e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.055 on 98 degrees of freedom
Multiple R-squared: 0.227, Adjusted R-squared: 0.2191
F-statistic: 28.78 on 1 and 98 DF, p-value: 5.42e-07
p 值几乎为 0,可以拒绝零假设
y 对 x2
lm_fit_x2 <- lm(y ~ x2)
summary(lm_fit_x2)
Call:
lm(formula = y ~ x2)
Residuals:
Min 1Q Median 3Q Max
-2.74970 -0.68815 -0.03074 0.66090 2.34837
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.3789 0.3845 3.587 0.000525 ***
x2 1.9529 0.3639 5.367 5.36e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.055 on 98 degrees of freedom
Multiple R-squared: 0.2272, Adjusted R-squared: 0.2193
F-statistic: 28.81 on 1 and 98 DF, p-value: 5.361e-07
p 值几乎为 0,可以拒绝零假设
错误观测
x1 <- c(x1, 0.1)
x2 <- c(x2, 0.8)
y <- c(y, 6)
多变量
y 对 x1 和 x2
lm_fit_v2 <- lm(y ~ x1 + x2)
summary(lm_fit_v2)
Call:
lm(formula = y ~ x1 + x2)
Residuals:
Min 1Q Median 3Q Max
-2.77906 -0.72031 -0.05796 0.62800 3.04112
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.5360 0.6115 2.512 0.0136 *
x1 0.1292 1.2407 0.104 0.9173
x2 1.7624 1.1500 1.532 0.1286
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.099 on 98 degrees of freedom
Multiple R-squared: 0.201, Adjusted R-squared: 0.1847
F-statistic: 12.32 on 2 and 98 DF, p-value: 1.682e-05
plot(lm_fit_v2)
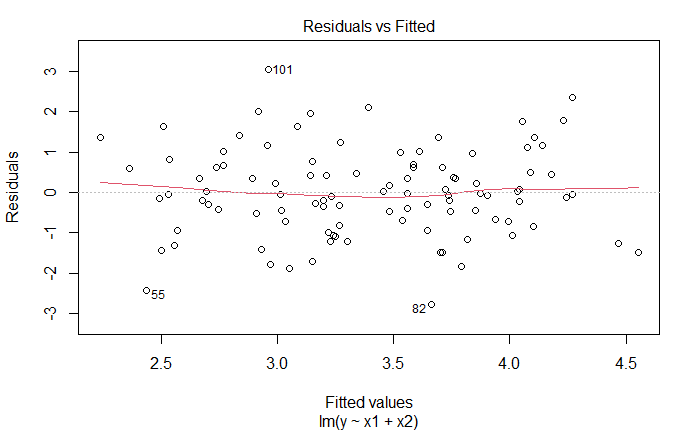
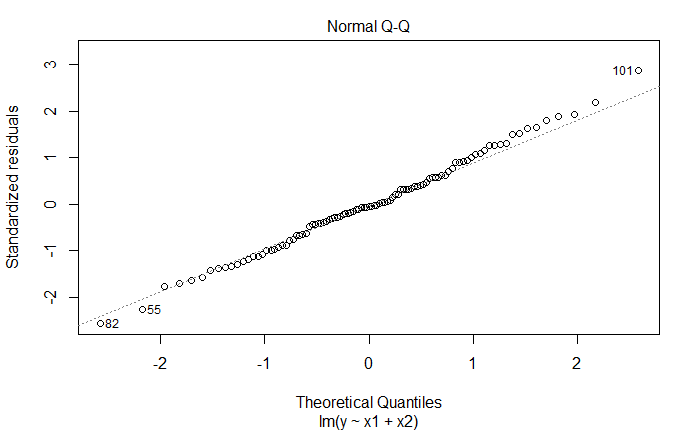
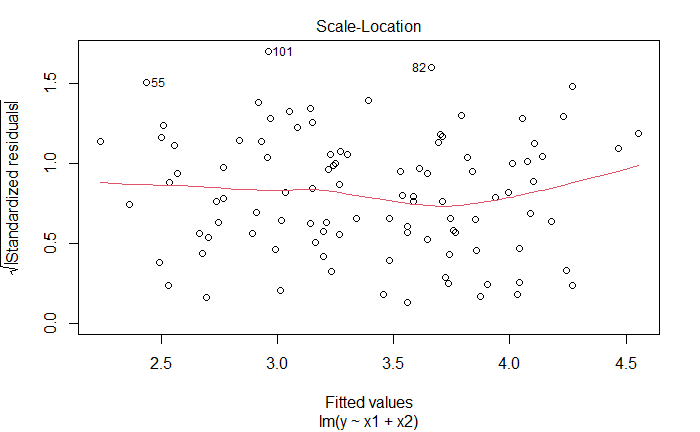
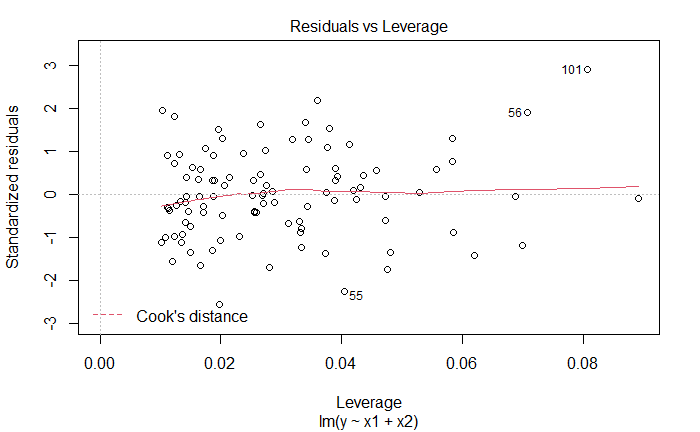
新增观测是离群点,也是高杠杆点
单变量
y 对 x1
lm_fit_x1_v2 <- lm(y ~ x1)
summary(lm_fit_x1_v2)
Call:
lm(formula = y ~ x1)
Residuals:
Min 1Q Median 3Q Max
-2.8899 -0.6553 -0.0917 0.5679 3.4070
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.4005 0.2378 10.09 < 2e-16 ***
x1 1.9251 0.4104 4.69 8.74e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.106 on 99 degrees of freedom
Multiple R-squared: 0.1818, Adjusted R-squared: 0.1736
F-statistic: 22 on 1 and 99 DF, p-value: 8.744e-06
plot(lm_fit_x1_v2)
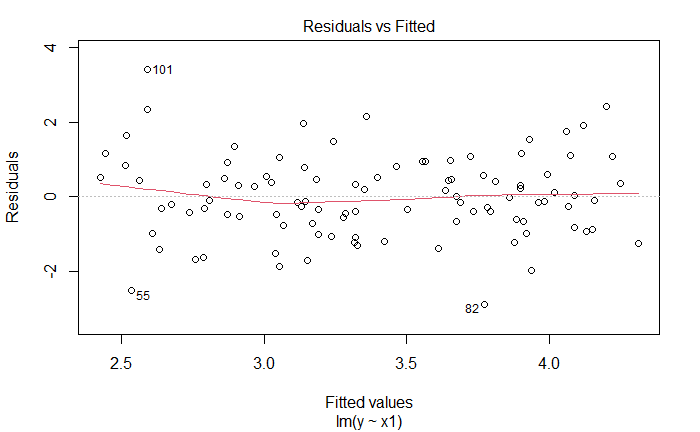
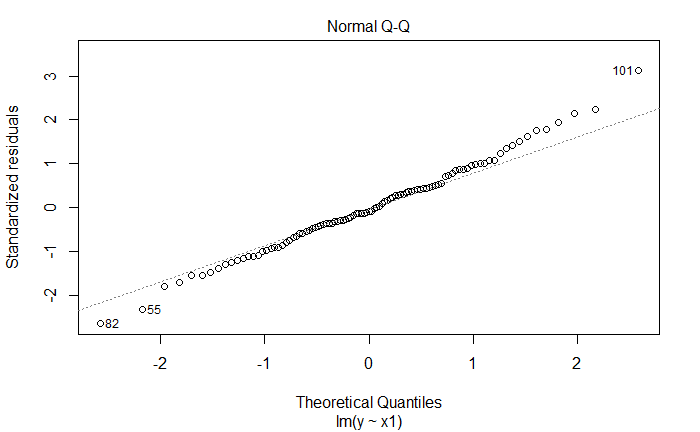
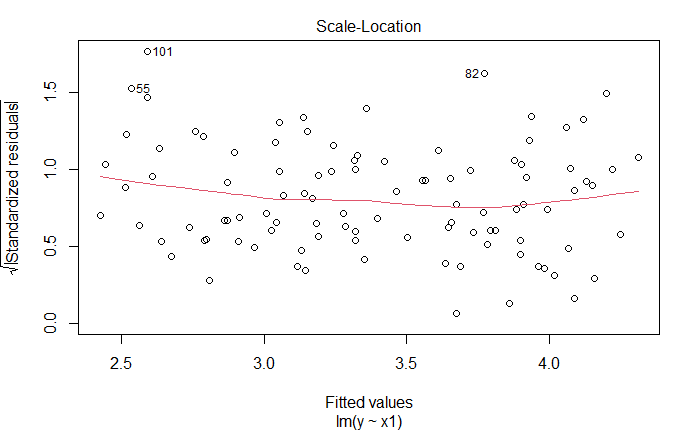
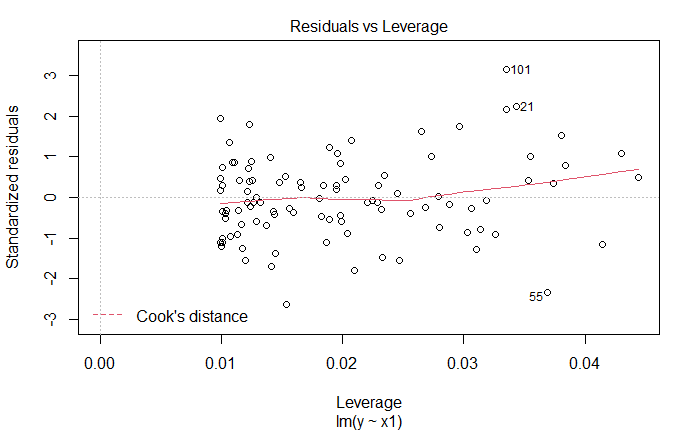
新增观测是离群点,也是高杠杆点
y 对 x2
lm_fit_x2_v2 <- lm(y ~ x2)
summary(lm_fit_x2_v2)
Call:
lm(formula = y ~ x2)
Residuals:
Min 1Q Median 3Q Max
-2.76917 -0.70920 -0.04555 0.64028 3.01186
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.4877 0.3964 3.753 0.000295 ***
x2 1.8755 0.3760 4.989 2.6e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.093 on 99 degrees of freedom
Multiple R-squared: 0.2009, Adjusted R-squared: 0.1928
F-statistic: 24.89 on 1 and 99 DF, p-value: 2.601e-06
plot(lm_fit_x2_v2)
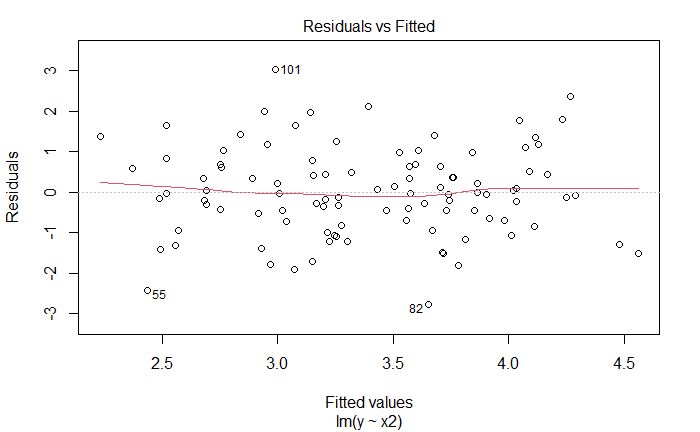
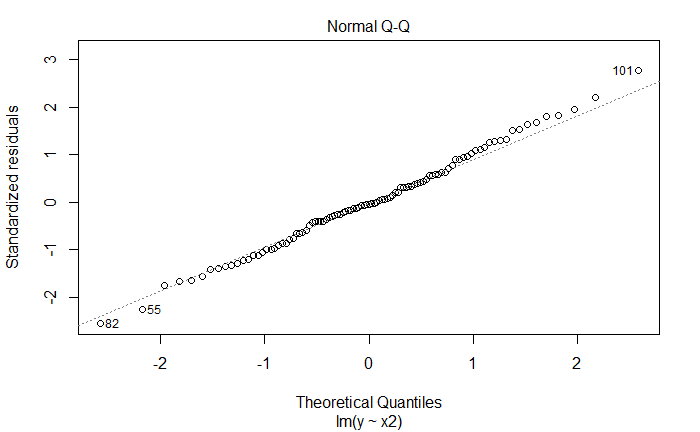
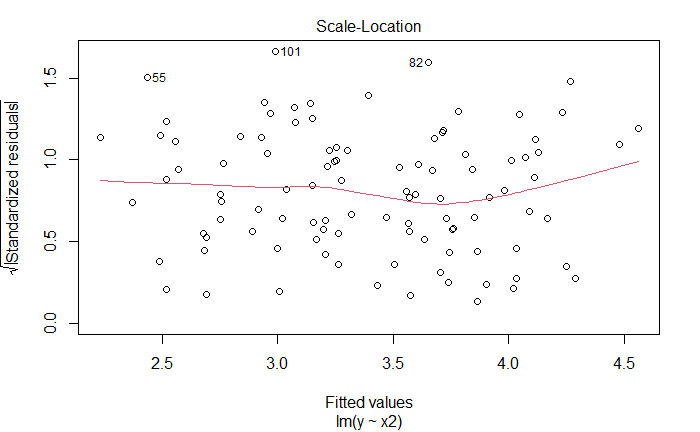
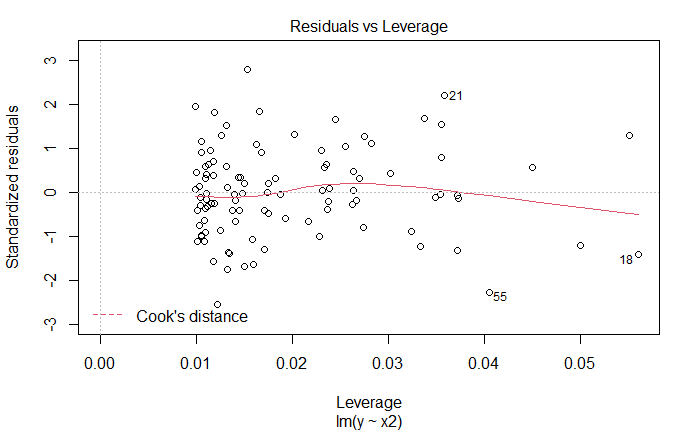
新增观测是离群点,但不是高杠杆点
参考
https://github.com/perillaroc/islr-study
ISLR实验系列文章
线性回归
分类
重抽样方法
线性模型选择与正则化
