ISLR习题:线性回归 - Auto数据集
目录
本文源自《统计学习导论:基于R语言应用》(ISLR) 第三章习题
library(ISLR)
head(Auto)
mpg cylinders displacement horsepower weight acceleration year origin name
1 18 8 307 130 3504 12.0 70 1 chevrolet chevelle malibu
2 15 8 350 165 3693 11.5 70 1 buick skylark 320
3 18 8 318 150 3436 11.0 70 1 plymouth satellite
4 16 8 304 150 3433 12.0 70 1 amc rebel sst
5 17 8 302 140 3449 10.5 70 1 ford torino
6 15 8 429 198 4341 10.0 70 1 ford galaxie 500
attach(Auto)
简单线性回归
mpg (油耗) 是响应变量,horsepower (马力) 是预测变量
创建模型
lm_fit = lm(horsepower ~ mpg)
lm_fit
Call:
lm(formula = horsepower ~ mpg)
Coefficients:
(Intercept) mpg
194.476 -3.839
查看模型
summary(lm_fit)
Call:
lm(formula = horsepower ~ mpg)
Residuals:
Min 1Q Median 3Q Max
-64.892 -15.716 -2.094 13.108 96.947
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 194.4756 3.8732 50.21 <2e-16 ***
mpg -3.8389 0.1568 -24.49 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 24.19 on 390 degrees of freedom
Multiple R-squared: 0.6059, Adjusted R-squared: 0.6049
F-statistic: 599.7 on 1 and 390 DF, p-value: < 2.2e-16
简要分析
预测变量与响应变量之间有关联
Pr 值接近 0,两者有很强的相关性
mpg 的系数为负,两者负相关
预测
mpg 为 98 时,计算预测值
predict(lm_fit, data.frame(mpg=c(98)))
1
-181.7354
计算置信区间
predict(
lm_fit,
data.frame(mpg=c(98)),
interval="confidence"
)
fit lwr upr
1 -181.7354 -204.8381 -158.6327
计算预测区间
predict(
lm_fit,
data.frame(mpg=c(98)),
interval="prediction"
)
fit lwr upr
1 -181.7354 -234.6145 -128.8562
关系图
plot(mpg, horsepower)
abline(lm_fit)
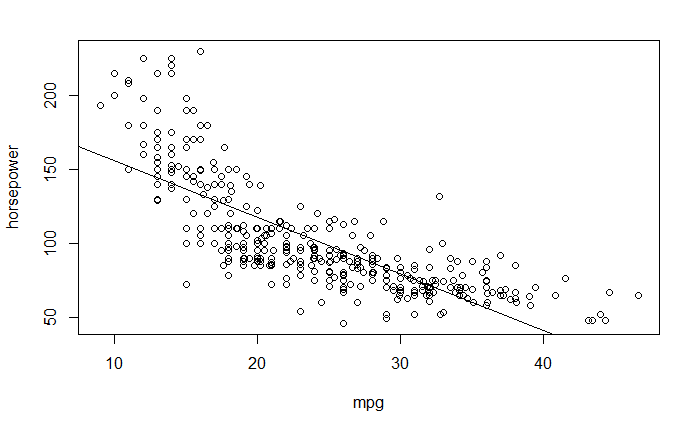
诊断图
使用 plot() 生成最小二乘回归拟合的诊断图
plot(lm_fit)
残差图
Residuals vs Fitted
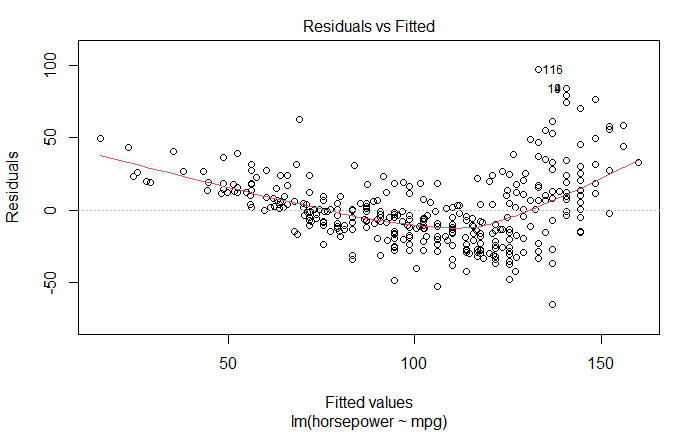
图中有明显的规律,残差值与估计值有关,说明线性模型的某些方面可能存在问题。
正态 QQ 图
Normal Q-Q
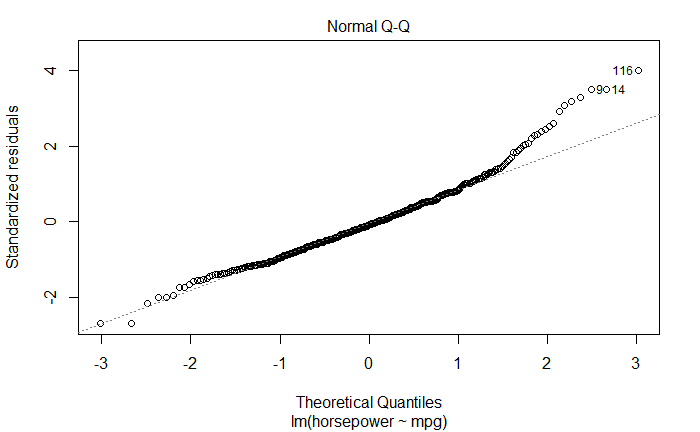
如果满足正态性假设,残差也应该是一个均值为 0 的正态分布,图上的点应该落在呈 45 度角的直线上。
Scale-Location
与第一幅图类似,显示标准化残差与估计值的关系。
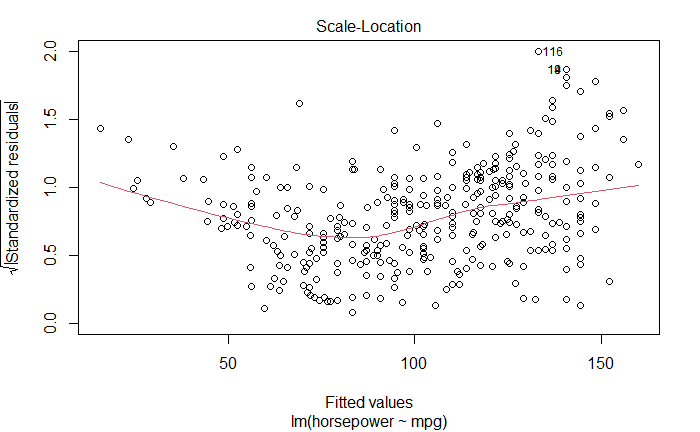
图中有比较明显的趋势,同样说明模型有问题。
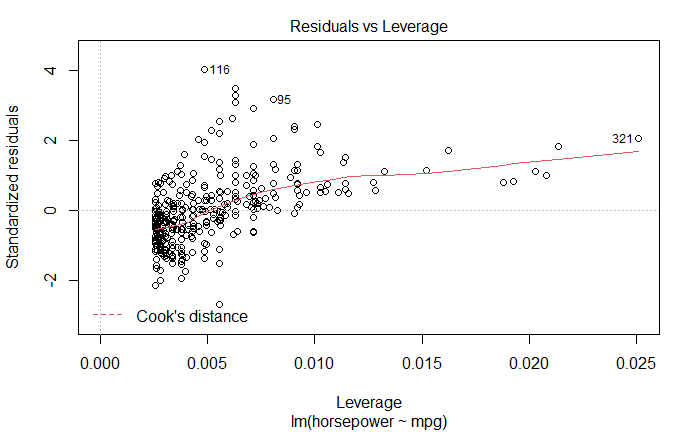
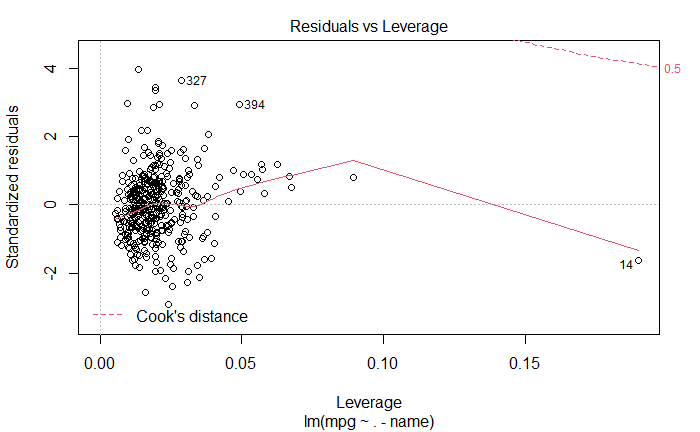
Residuals vs Leverage
杠杆统计量与学生化残差的关系图,用于查看离群点和高杠杆点。
多元线性回归
散点矩阵图
plot(Auto[, -c(9)])
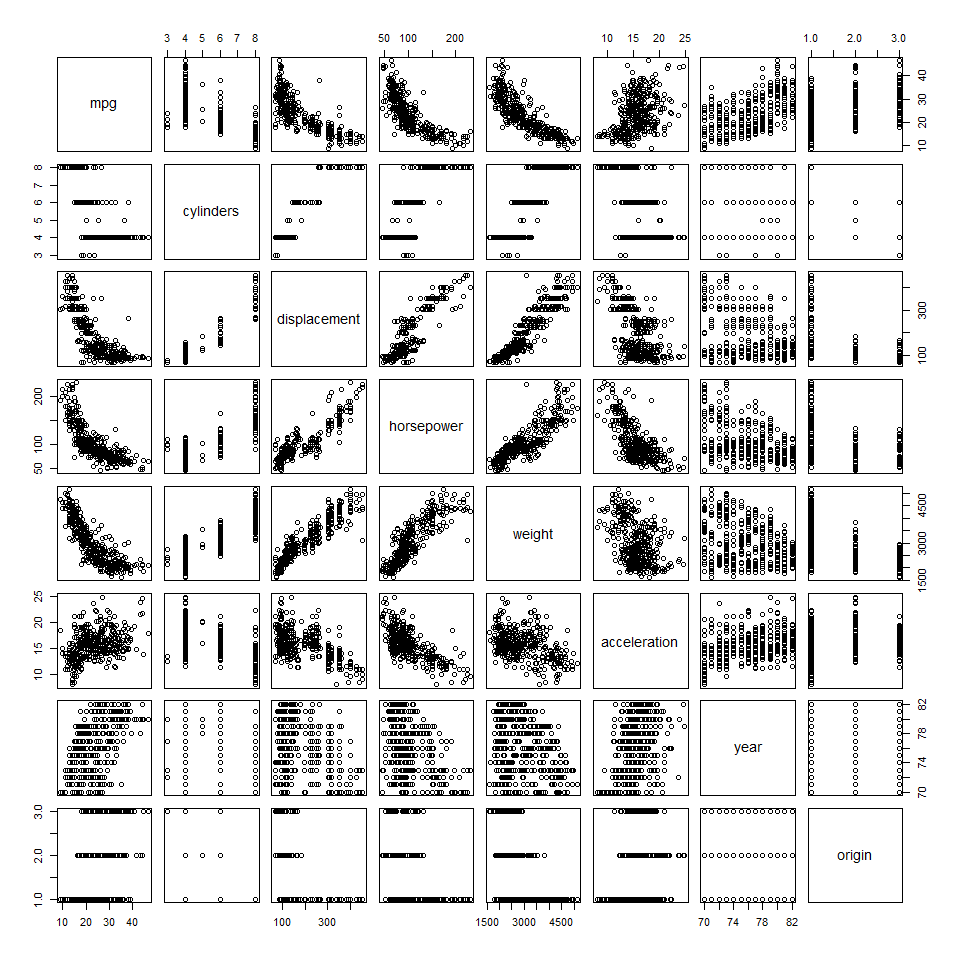
相关系数矩阵
data.frame(cor(Auto[,-9]))
mpg cylinders displacement horsepower weight acceleration year origin
mpg 1.0000000 -0.7776175 -0.8051269 -0.7784268 -0.8322442 0.4233285 0.5805410 0.5652088
cylinders -0.7776175 1.0000000 0.9508233 0.8429834 0.8975273 -0.5046834 -0.3456474 -0.5689316
displacement -0.8051269 0.9508233 1.0000000 0.8972570 0.9329944 -0.5438005 -0.3698552 -0.6145351
horsepower -0.7784268 0.8429834 0.8972570 1.0000000 0.8645377 -0.6891955 -0.4163615 -0.4551715
weight -0.8322442 0.8975273 0.9329944 0.8645377 1.0000000 -0.4168392 -0.3091199 -0.5850054
acceleration 0.4233285 -0.5046834 -0.5438005 -0.6891955 -0.4168392 1.0000000 0.2903161 0.2127458
year 0.5805410 -0.3456474 -0.3698552 -0.4163615 -0.3091199 0.2903161 1.0000000 0.1815277
origin 0.5652088 -0.5689316 -0.6145351 -0.4551715 -0.5850054 0.2127458 0.1815277 1.0000000
多元线性回归
lm_fit_multi <- lm(mpg~.-name, data=Auto)
summary(lm_fit_multi)
Call:
lm(formula = mpg ~ . - name, data = Auto)
Residuals:
Min 1Q Median 3Q Max
-9.5903 -2.1565 -0.1169 1.8690 13.0604
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -17.218435 4.644294 -3.707 0.00024 ***
cylinders -0.493376 0.323282 -1.526 0.12780
displacement 0.019896 0.007515 2.647 0.00844 **
horsepower -0.016951 0.013787 -1.230 0.21963
weight -0.006474 0.000652 -9.929 < 2e-16 ***
acceleration 0.080576 0.098845 0.815 0.41548
year 0.750773 0.050973 14.729 < 2e-16 ***
origin 1.426141 0.278136 5.127 4.67e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.328 on 384 degrees of freedom
Multiple R-squared: 0.8215, Adjusted R-squared: 0.8182
F-statistic: 252.4 on 7 and 384 DF, p-value: < 2.2e-16
- 预测变量和响应变量之间是否有关系?
F 统计量为 252.4,远大于 1,且 F 统计量的 p 值几乎为零。 说明至少一个预测变量与响应变量有关系。
- 哪个预测变量与响应变量在统计上具有显著关系?
从预测变量的 p 值看,displacement,weight,year 和 origin 的 p 值较小,与响应变量具有显著关系。
- year 车龄变量的系数说明什么?
year 的系数为正值,说明随着车龄增长,油耗会增加。
诊断图
plot(lm_fit_multi)
- 残差图是否有异常大的离群点?
有异常点,图中已标明
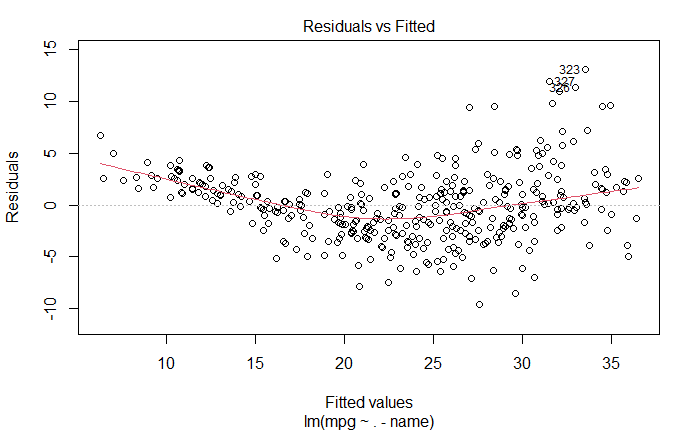
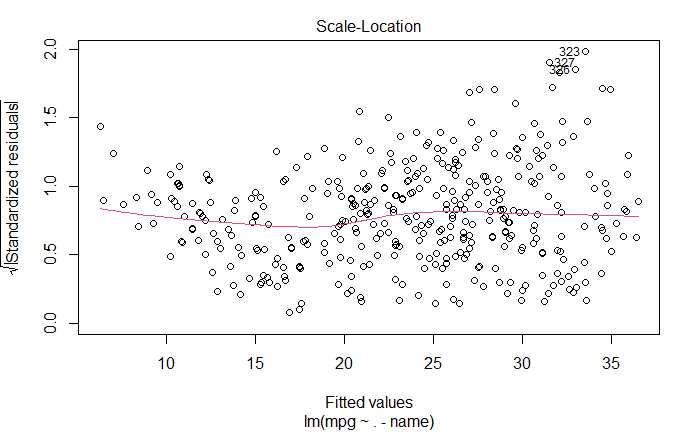
- 杠杆图是否识别出了有异常高杠杆作用的点么?
已标明,第 14 个样本
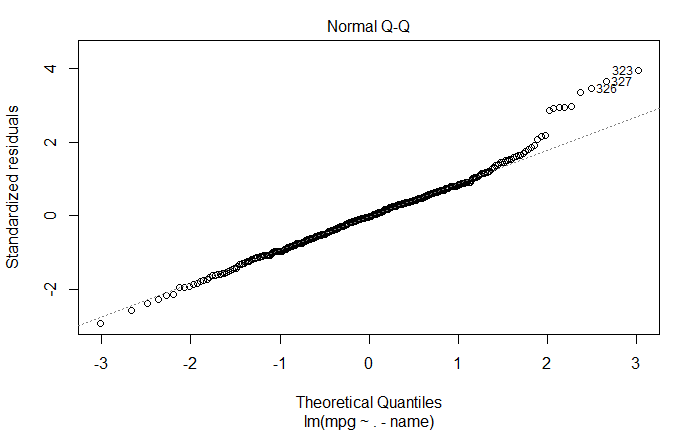
- Normal Q-Q
残差不按正态分布
交互作用
lm_fit_inter <- lm(
mpg ~ .-name + cylinders * horsepower,
data=Auto
)
summary(lm_fit_inter)
Call:
lm(formula = mpg ~ . - name + cylinders * horsepower, data = Auto)
Residuals:
Min 1Q Median 3Q Max
-9.2399 -1.6871 -0.0511 1.2858 11.9380
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.7025260 4.9115648 2.383 0.017676 *
cylinders -4.3060695 0.4580950 -9.400 < 2e-16 ***
displacement -0.0013925 0.0069110 -0.201 0.840426
horsepower -0.3156601 0.0306339 -10.304 < 2e-16 ***
weight -0.0038948 0.0006231 -6.250 1.09e-09 ***
acceleration -0.1703028 0.0901427 -1.889 0.059612 .
year 0.7393193 0.0448736 16.476 < 2e-16 ***
origin 0.9031644 0.2496880 3.617 0.000338 ***
cylinders:horsepower 0.0402008 0.0037856 10.619 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.929 on 383 degrees of freedom
Multiple R-squared: 0.8621, Adjusted R-squared: 0.8592
F-statistic: 299.3 on 8 and 383 DF, p-value: < 2.2e-16
存在统计显著的交互项,不过系数较小。
非线性变换
lm_fit_non_linear <- lm(
mpg ~ .-name + log(horsepower),
data=Auto
)
summary(lm_fit_non_linear)
Call:
lm(formula = mpg ~ . - name + log(horsepower), data = Auto)
Residuals:
Min 1Q Median 3Q Max
-8.5777 -1.6623 -0.1213 1.4913 12.0230
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.674e+01 1.106e+01 7.839 4.54e-14 ***
cylinders -5.530e-02 2.907e-01 -0.190 0.849230
displacement -4.607e-03 7.108e-03 -0.648 0.517291
horsepower 1.764e-01 2.269e-02 7.775 7.05e-14 ***
weight -3.366e-03 6.561e-04 -5.130 4.62e-07 ***
acceleration -3.277e-01 9.670e-02 -3.388 0.000776 ***
year 7.421e-01 4.534e-02 16.368 < 2e-16 ***
origin 8.976e-01 2.528e-01 3.551 0.000432 ***
log(horsepower) -2.685e+01 2.652e+00 -10.127 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.959 on 383 degrees of freedom
Multiple R-squared: 0.8592, Adjusted R-squared: 0.8562
F-statistic: 292.1 on 8 and 383 DF, p-value: < 2.2e-16
horsepower 的对数项 p 值几乎为 0,说明部分预测变量与响应变量之间有非线性关系。
参考
https://github.com/perillaroc/islr-study
ISLR实验系列文章
线性回归
分类
重抽样方法
线性模型选择与正则化
