预测雷暴旋转的基础机器学习:分类 - 性能图
本文翻译自 AMS 机器学习 Python 教程,并有部分修改。
Lagerquist, R., and D.J. Gagne II, 2019: “Basic machine learning for predicting thunderstorm rotation: Python tutorial”. https://github.com/djgagne/ams-ml-python-course/blob/master/module_2/ML_Short_Course_Module_2_Basic.ipynb.
本文接上一篇文章,介绍如何绘制性能图 (Performance diagram) 评估二元分类问题。
性能图
引自
Performance Diagram
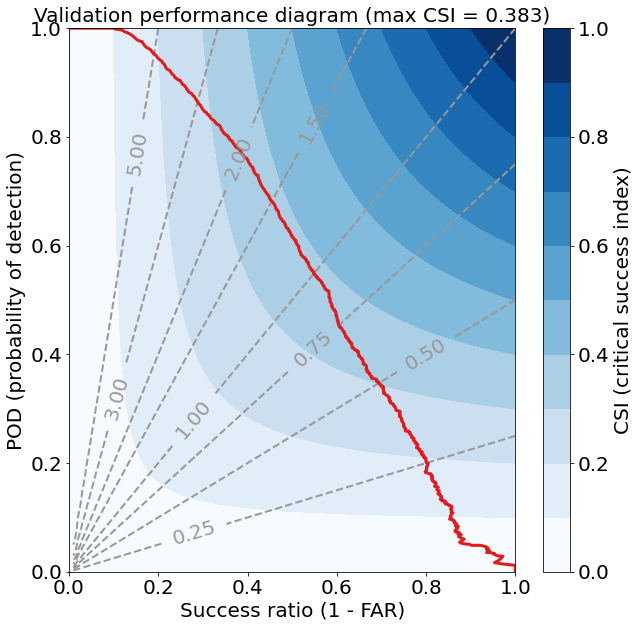
验证数据集上的性能图如下所示
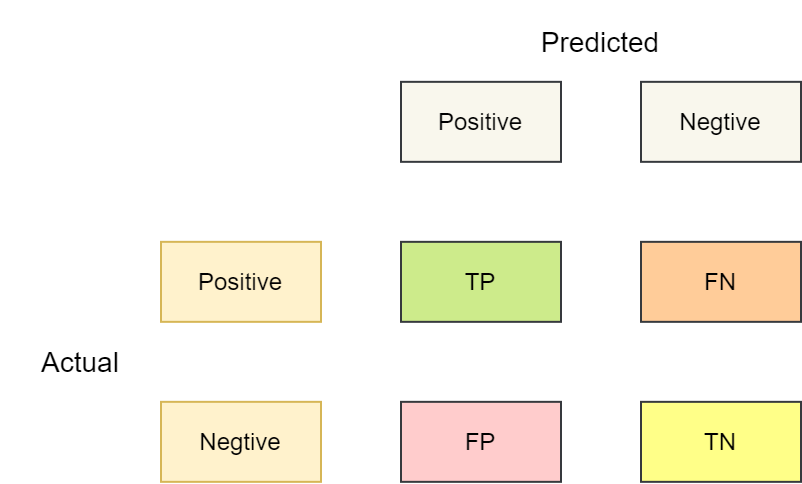
混淆矩阵
二分类问题的混淆矩阵
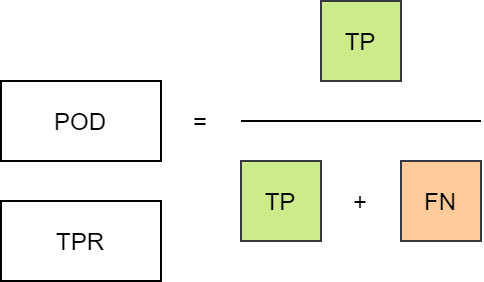
POD
真阳率
Probability of detection (hit rate),POD
回答如下问题:有多少观察到"是"的事件被正确预测?
范围:0 到 1
完美分数:1
特性:
对 hits (TP) 敏感,但忽略 false alarm (FP)。 对事件的气候频率非常敏感。 适用于罕见事件。 可以通过发布更多“是”预测来增加 hits 次数,从而人为地加以改进。 应与 false alarm ratio 结合使用。 POD 还是广泛用于概率预测的Relative Operating Characteristic (ROC) 的重要组成部分。
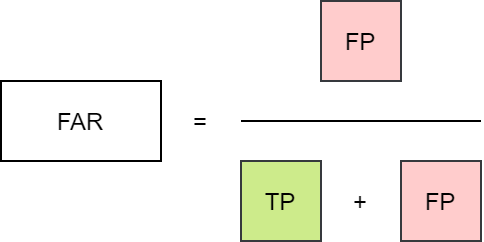
SR
False alarm ratio, FAR
回答如下问题:预测"是"事件中,哪些部分实际上未发生(即误报)?
范围:0 到 1
完美分数:0
特性:
对 false alarm (FP) 敏感,但忽略 miss (FN)。 对事件的气候频率非常敏感。 应与 POD 结合使用。
Success ratio,SR
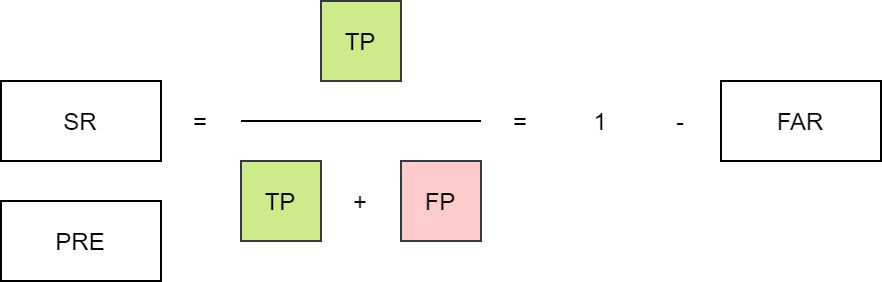
回答如下问题:预测为"是"的事件中哪些部分观测也是“是”?
范围:0 到 1
完美分数:1
特性:
给出有关观察到的事件的可能性的信息(假设已被预测)。 它对 false alarm (FP) 很敏感,但忽略 miss (FN)。 SR 等于 1-FAR。 在分类性能图 (categorical performance diagram) 中,相对于 SR 绘制了 POD。
CSI
Threat score (TS),Critical success index (CSI)
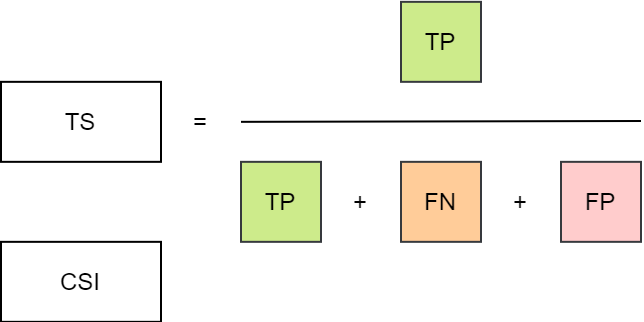
回答如下问题:预测的“是”事件与观察到的“是”事件对应得如何?
范围:0 到 1,0 表示没有技巧
完美分数:0
特性:
测量正确预测的观测和/或预测事件的比例。 在不考虑真反例的情况下,可以被当成精确度,也就是说,TS 仅关注有计数的预测。 对 hits (TP) 敏感,对 misses (FN) 和 false alarms (FP) 都会造成惩罚。 不区分预测误差的来源。 取决于事件的气候频率(罕见事件的评分较低),因为某些 hits 可能纯粹是由于随机机会而发生的。
frequency bias
Bias score, frequency bias
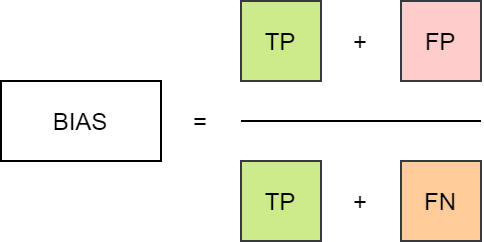
回答如下问题:“是”事件的预测频率与观察到的“是”事件的频率相比如何?
范围:0 到 正无穷大
完美分数:1
特性:
测量预测事件的频率与观察到的事件的频率之比。 指示预测系统是倾向于发生低预测 (BIAS < 1) 还是发生高预测 (BIAS > 1) 事件。 不衡量预测与观测值的对应程度,仅衡量相对频率。
Performance Diagram
在概念上类似于 Taylor diagram 的方法中,有可能利用二分预测性能的四个度量之间的几何关系:probability of detection (POD),false alarm ratio 或与其相反,success ratio (SR),bias 和 critical success index (CSI;也称为 threat score,即 TS)。 Roebber(2009)给出了该图的推导细节。
对于良好的预测,POD,SR,bias 和 CSI 趋于一致,因此,完美的预测位于图表的右上方。 特定方向的偏差将指示 POD 和 SR 的相对差异,并因此指示 bias 和 CSI。 因此,可以立即看到性能差异。 准确度的最佳提高是通过沿 45 度移动来实现的,也就是说,通过同时增加检测和减少误报来保持无偏的预测。 通过相对于参考预测(气候,持续性或任何其他所需基准)绘制预测质量度量来评估技能。
采样变异性的影响是使用一种重采样的形式来估计的,该替换具有从验证数据中进行 bootstrap 替换。 SR 和 POD 的第 95 个百分位范围被绘制为围绕验证点的“十字线”,并且同时显示了 bias 和 CSI 的变化。 使用观察和预测的“是”和“否”条目(即边际频率)的采样频率创建了与原始大小相同的 1000 个新样本,并从这些“气候”样本中计算了第 25 和第 975 精度度量,产生第 95 个百分位范围。
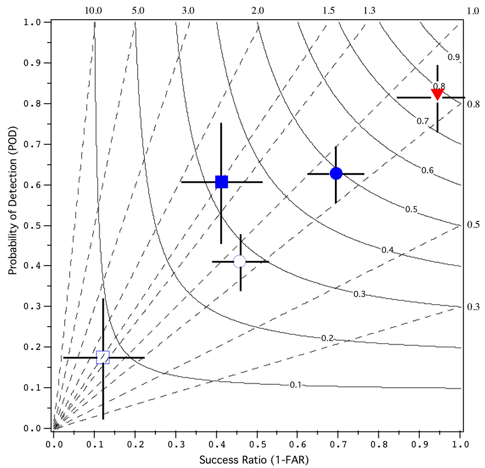
在示例图中,来自Roebber el al.(2003) 的大雪密度和小雪密度验证数据(分别为实心蓝色正方形和圆形)以及相应的采样频率(分别为空心蓝色正方形和圆形)。 还显示了 Fowle 和 Roebber (2003)(红色三角形)对流发生的 48 小时预报验证。
参考
Fowle, M.A. and P.J. Roebber, 2003: Short-range (0-48 h) numerical prediction of convective occurrence, mode, and location. Wea. Forecasting, 18, 782-794.
Roebber, P.J., 2009: Visualizing multiple measures of forecast quality. Wea. Forecasting, 24, 601-608.
Roebber, P.J., S.L. Breuning, D.M. Schultz, and J.V. Cortinas, Jr., 2003: Improving snowfall forecasting by diagnosing snow density. Wea. Forecasting, 18, 264-287.
计算性能图数据
get_points_in_perf_diagram 为性能图计算点,返回
- 真正例率(TPR)
- 查准率(PRE)
def get_points_in_perf_diagram(
observed_labels: np.ndarray,
forecast_probabilities: np.ndarray,
) -> (np.ndarray, np.ndarray):
# 验证数据范围
assert np.all(np.logical_or(
observed_labels == 0, observed_labels == 1
))
assert np.all(np.logical_and(
forecast_probabilities >= 0, forecast_probabilities <= 1
))
observed_labels = observed_labels.astype(int)
binarization_thresholds = np.linspace(
0, 1,
num=1001,
dtype=float
)
num_thresholds = len(binarization_thresholds)
pod_by_threshold = np.full(num_thresholds, np.nan)
success_ratio_by_threshold = np.full(num_thresholds, np.nan)
for k in range(num_thresholds):
these_forecast_labels = (
forecast_probabilities >= binarization_thresholds[k]
).astype(int)
# 真阳性 TP
this_num_hits = np.sum(np.logical_and(
these_forecast_labels == 1, observed_labels == 1
))
# 假阳性 FP
this_num_false_alarms = np.sum(np.logical_and(
these_forecast_labels == 1, observed_labels == 0
))
# 假阴性 FN
this_num_misses = np.sum(np.logical_and(
these_forecast_labels == 0, observed_labels == 1
))
try:
# 真阳率 TPR = TP / (TP + FN)
pod_by_threshold[k] = (
float(this_num_hits) / (this_num_hits + this_num_misses)
)
except ZeroDivisionError:
pass
try:
# 精度 PRE = TP / (TP + FP)
success_ratio_by_threshold[k] = (
float(this_num_hits) / (this_num_hits + this_num_false_alarms)
)
except ZeroDivisionError:
pass
pod_by_threshold = np.array([1.] + pod_by_threshold.tolist() + [0.])
success_ratio_by_threshold = np.array(
[0.] + success_ratio_by_threshold.tolist() + [1.]
)
return pod_by_threshold, success_ratio_by_threshold绘制性能图
plot_performance_diagram 绘制性能图
def plot_performance_diagram(
observed_labels,
forecast_probabilities,
line_colour=np.array([228, 26, 28], dtype=float) / 255,
line_width=3,
bias_line_colour=np.full(3, 152. / 255),
bias_line_width=2,
axes_object=None
):
# 获取真阳率(TPR)和精度(PRE)
pod_by_threshold, success_ratio_by_threshold = get_points_in_perf_diagram(
observed_labels=observed_labels,
forecast_probabilities=forecast_probabilities
)
if axes_object is None:
_, axes_object = pyplot.subplots(
1, 1,
figsize=(10, 10)
)
# 创建 精度 / 真阳率 坐标网格
success_ratio_matrix, pod_matrix = _get_sr_pod_grid()
# CSI
csi_matrix = _csi_from_sr_and_pod(
success_ratio_matrix,
pod_matrix
)
# 频率偏差
frequency_bias_matrix = _bias_from_sr_and_pod(
success_ratio_matrix,
pod_matrix
)
this_colour_map_object, this_colour_norm_object = _get_csi_colour_scheme()
# 绘制 CSI 的填充图
pyplot.contourf(
success_ratio_matrix,
pod_matrix,
csi_matrix,
np.linspace(0, 1, num=11, dtype=float),
cmap=this_colour_map_object,
norm=this_colour_norm_object,
vmin=0.,
vmax=1.,
axes=axes_object
)
# 为 CSI 填充图添加颜色条
colour_bar_object = _add_colour_bar(
axes_object=axes_object,
colour_map_object=this_colour_map_object,
colour_norm_object=this_colour_norm_object,
values_to_colour=csi_matrix,
min_colour_value=0.,
max_colour_value=1.,
orientation_string='vertical',
extend_min=False,
extend_max=False
)
colour_bar_object.set_label('CSI (critical success index)')
LEVELS_FOR_BIAS_CONTOURS = np.array([0.25, 0.5, 0.75, 1., 1.5, 2., 3., 5.])
bias_colour_tuple = ()
for _ in range(len(LEVELS_FOR_BIAS_CONTOURS)):
bias_colour_tuple += (bias_line_colour,)
# 绘制频率偏差等值线(虚线)
bias_contour_object = pyplot.contour(
success_ratio_matrix,
pod_matrix,
frequency_bias_matrix,
LEVELS_FOR_BIAS_CONTOURS,
colors=bias_colour_tuple,
linewidths=bias_line_width,
linestyles='dashed',
axes=axes_object,
)
# 为频率偏差等值线添加标签
pyplot.clabel(
bias_contour_object,
inline=True,
inline_spacing=10,
fmt='%.2f',
fontsize=20,
)
nan_flags = np.logical_or(
np.isnan(success_ratio_by_threshold),
np.isnan(pod_by_threshold)
)
# 绘制 精度 / 真阳率 线图
if not np.all(nan_flags):
real_indices = np.where(np.invert(nan_flags))[0]
axes_object.plot(
success_ratio_by_threshold[real_indices],
pod_by_threshold[real_indices],
color=line_colour,
linestyle='solid',
linewidth=line_width
)
axes_object.set_xlabel('Success ratio (1 - FAR)')
axes_object.set_ylabel('POD (probability of detection)')
axes_object.set_xlim(0., 1.)
axes_object.set_ylim(0., 1.)
return pod_by_threshold, success_ratio_by_threshold_get_sr_pod_grid 创建 SR-POD 坐标网格(success ratio / probability of detection,精度 / 真阳率)
def _get_sr_pod_grid(success_ratio_spacing=0.01, pod_spacing=0.01):
num_success_ratios = 1 + int(np.ceil(1. / success_ratio_spacing))
num_pod_values = 1 + int(np.ceil(1. / pod_spacing))
unique_success_ratios = np.linspace(0., 1., num=num_success_ratios)
unique_pod_values = np.linspace(0., 1., num=num_pod_values)[::-1]
return np.meshgrid(unique_success_ratios, unique_pod_values)_csi_from_sr_and_pod 函数计算 CSI(critical success index,临界成功指数)
def _csi_from_sr_and_pod(
success_ratio_array: np.ndarray,
pod_array: np.ndarray
) -> np.ndarray:
return (success_ratio_array ** -1 + pod_array ** -1 - 1.) ** -1_bias_from_sr_and_pod 函数根据精度和真阳率计算频率偏差
def _bias_from_sr_and_pod(
success_ratio_array,
pod_array
):
return pod_array / success_ratio_array_get_csi_colour_scheme 函数为 CSI 指数生成色表
def _get_csi_colour_scheme():
LEVELS_FOR_CSI_CONTOURS = np.linspace(0, 1, num=11, dtype=float)
this_colour_map_object = pyplot.cm.Blues
this_colour_norm_object = matplotlib.colors.BoundaryNorm(
LEVELS_FOR_CSI_CONTOURS,
this_colour_map_object.N
)
rgba_matrix = this_colour_map_object(
this_colour_norm_object(
LEVELS_FOR_CSI_CONTOURS
)
)
colour_list = [
rgba_matrix[i, ..., :-1] for i in range(rgba_matrix.shape[0])
]
colour_map_object = matplotlib.colors.ListedColormap(colour_list)
colour_map_object.set_under(np.array([1, 1, 1]))
colour_norm_object = matplotlib.colors.BoundaryNorm(
LEVELS_FOR_CSI_CONTOURS,
colour_map_object.N
)
return colour_map_object, colour_norm_object绘制 CSI 填充图的颜色条
colour_map_object, colour_norm_object = _get_csi_colour_scheme()
scalar_mappable_object = pyplot.cm.ScalarMappable(
cmap=colour_map_object,
norm=colour_norm_object
)
pyplot.colorbar(
mappable=scalar_mappable_object,
orientation='horizontal',
pad=0.075,
extend='both',
shrink=1
)
pyplot.gca().set_visible(False)
示例
dataset_name = "training"
pod_by_threshold, success_ratio_by_threshold = (
get_points_in_perf_diagram(
observed_labels=training_target_table["strong_future_rotation_flag"].values,
forecast_probabilities=training_probabilities
)
)
csi_by_threshold = (
(pod_by_threshold ** -1 + success_ratio_by_threshold ** -1 - 1) ** -1
)
max_csi = np.nanmax(csi_by_threshold)
_, axes_object = pyplot.subplots(
1, 1,
figsize=(
10,
10
)
)
plot_performance_diagram(
observed_labels=training_target_table["strong_future_rotation_flag"].values,
forecast_probabilities=training_probabilities,
axes_object=axes_object
)
pyplot.title(
f'{dataset_name} performance diagram '
f'(max CSI = {max_csi:.3f})'
)
pyplot.show()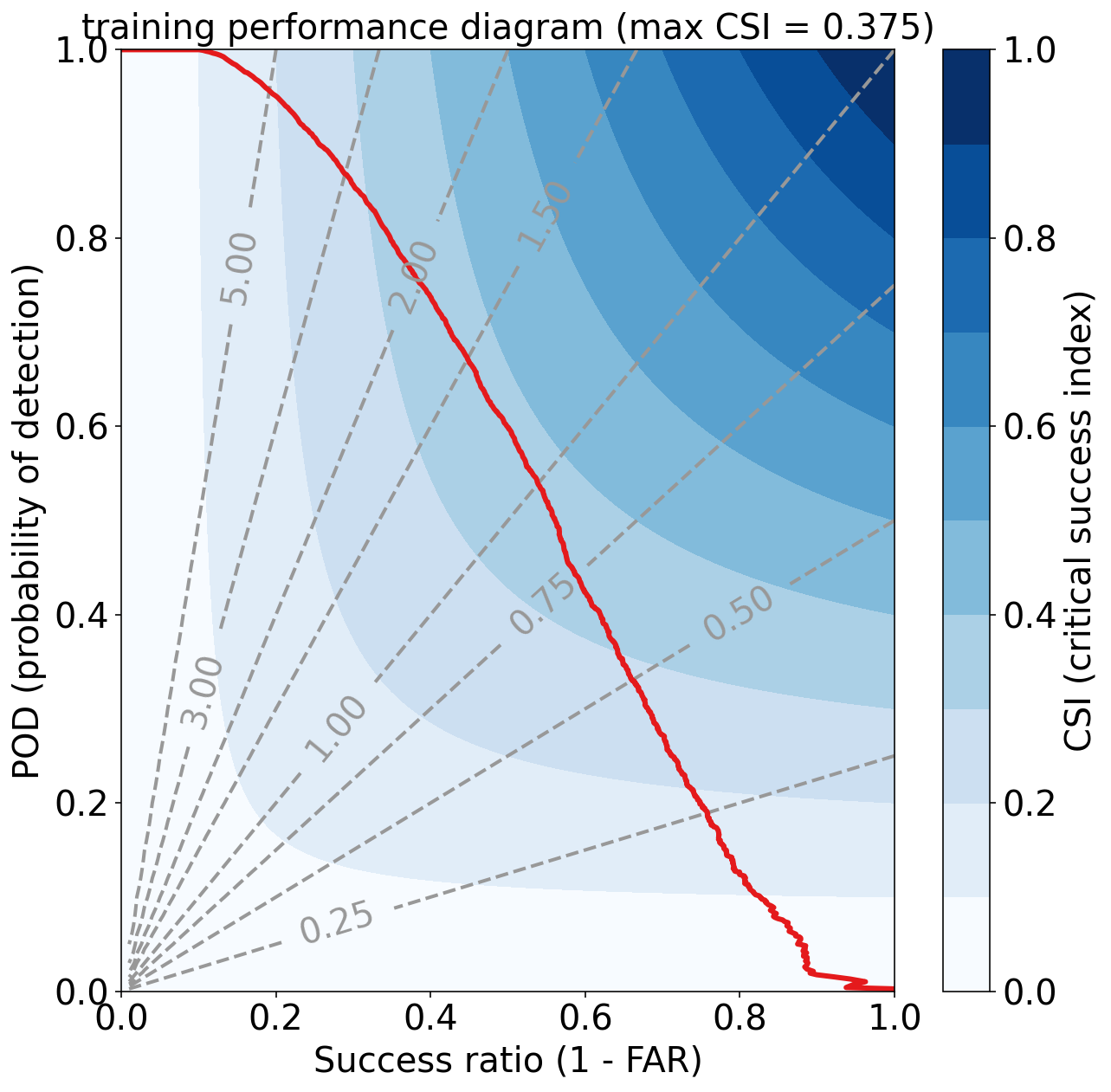
参考
https://github.com/djgagne/ams-ml-python-course
AMS 机器学习课程
数据预处理:
实际数据处理:
《AMS机器学习课程:预测雷暴旋转的基础机器学习 - 数据》
线性回归:
《AMS机器学习课程:预测雷暴旋转的基础机器学习 - 线性回归》
《AMS机器学习课程:预测雷暴旋转的基础机器学习 - 正则化》
《AMS机器学习课程:预测雷暴旋转的基础机器学习 - 超参数试验》
逻辑回归:
