预测雷暴旋转的基础机器学习:分类 - ROC 曲线
本文翻译自 AMS 机器学习 Python 教程,并有部分修改。
Lagerquist, R., and D.J. Gagne II, 2019: “Basic machine learning for predicting thunderstorm rotation: Python tutorial”. https://github.com/djgagne/ams-ml-python-course/blob/master/module_2/ML_Short_Course_Module_2_Basic.ipynb.
本文接上一篇文章,介绍如何绘制 ROC 曲线评估二元分类问题。
评估性能
utils 包中的 eval_binary_classifn 函数用于评估二元分类模型的性能,绘制三类图形。
本文介绍 ROC 曲线的绘制,下图是训练数据集的 ROC 曲线。
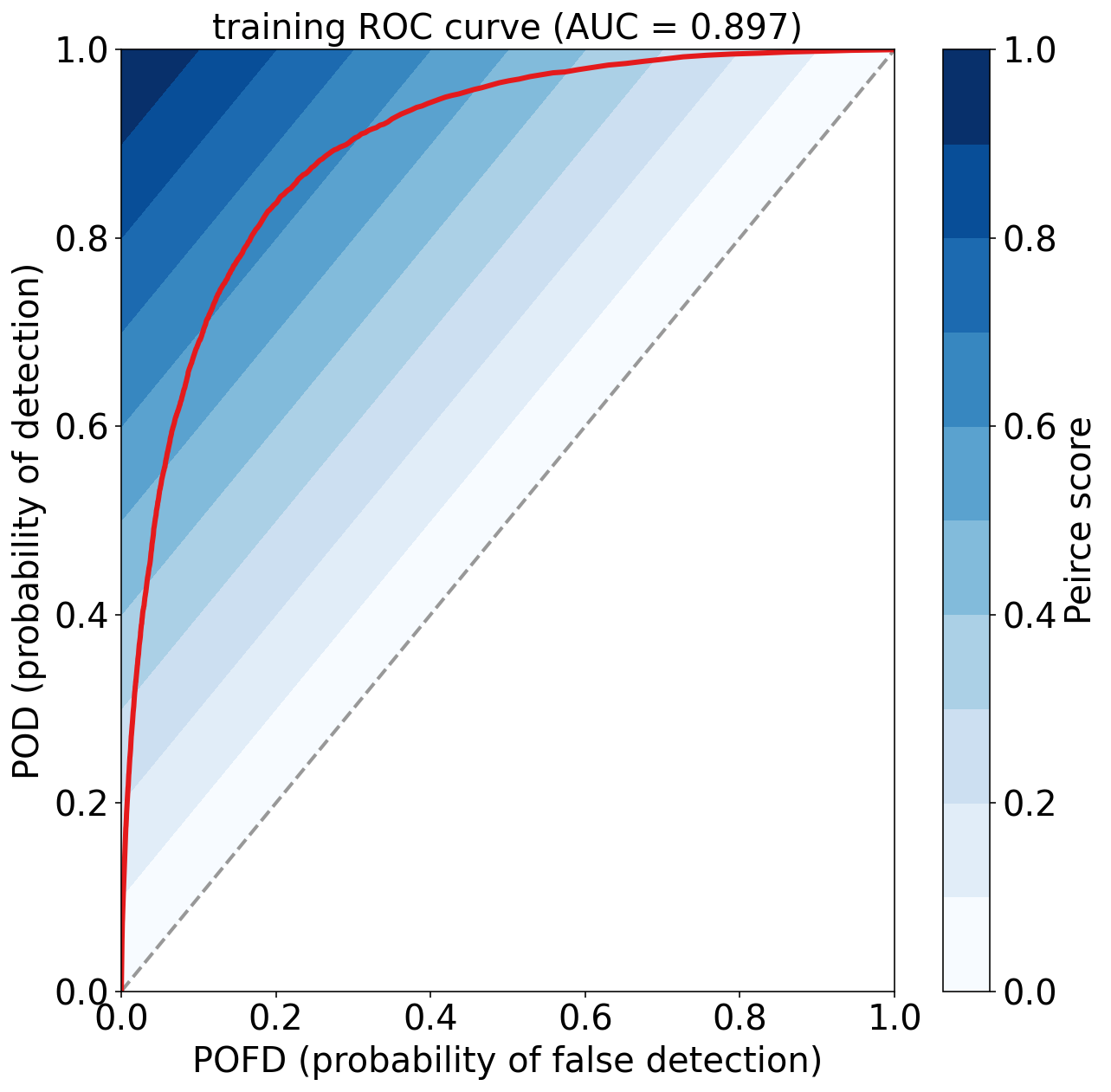
ROC 曲线
以下部分引自:
- 《机器学习》(周志华)
- 维基百科“ROC曲线”条目 https://zh.wikipedia.org/wiki/ROC%E6%9B%B2%E7%BA%BF
- https://www.cawcr.gov.au/projects/verification/
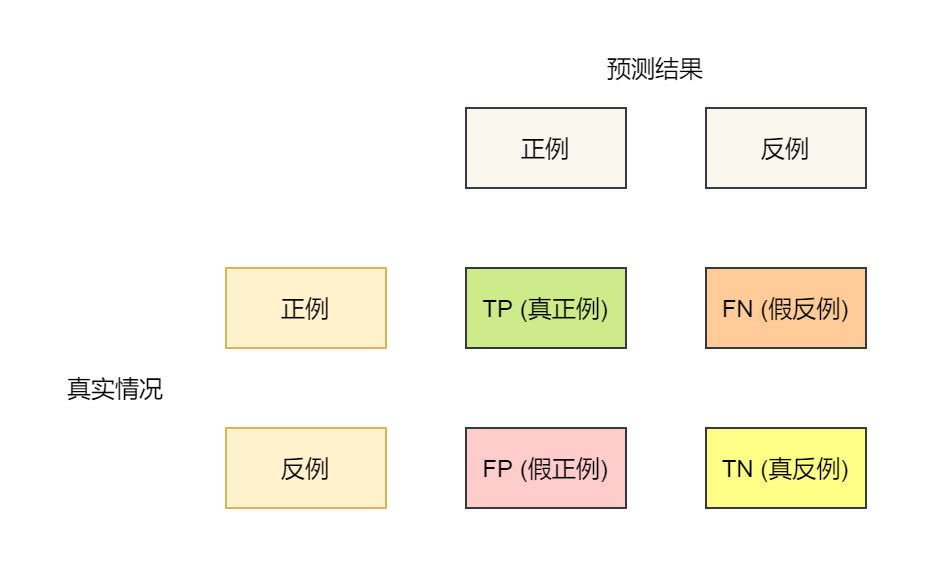
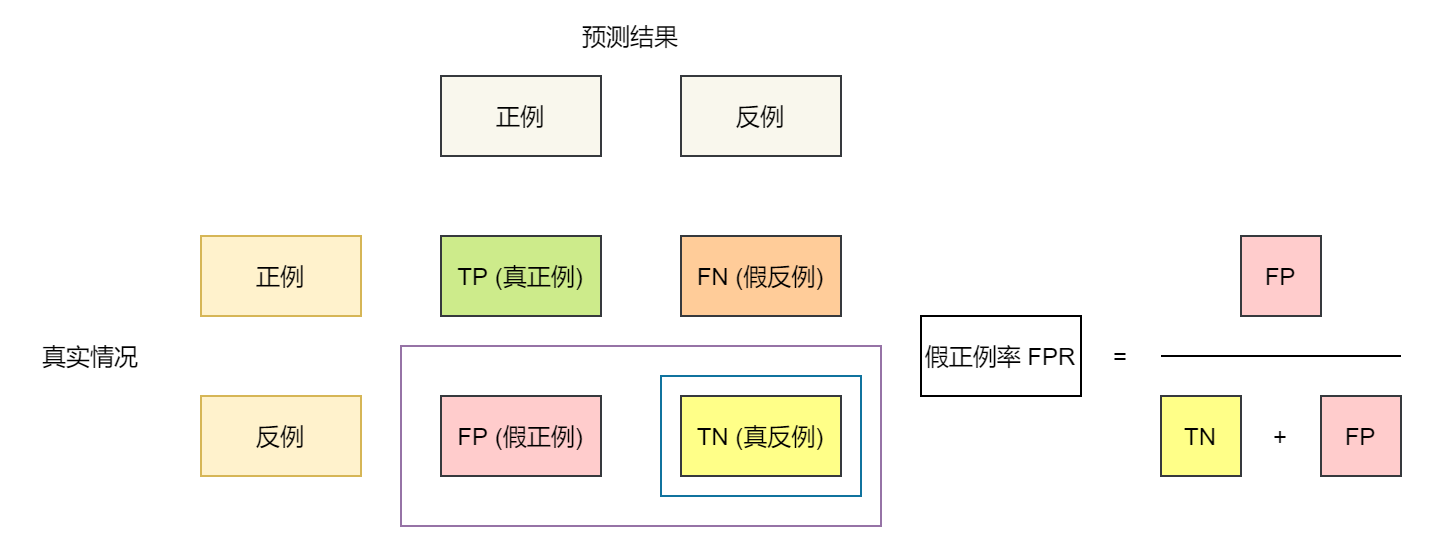
二分类问题分类结果的混淆矩阵 Confusion Matrix
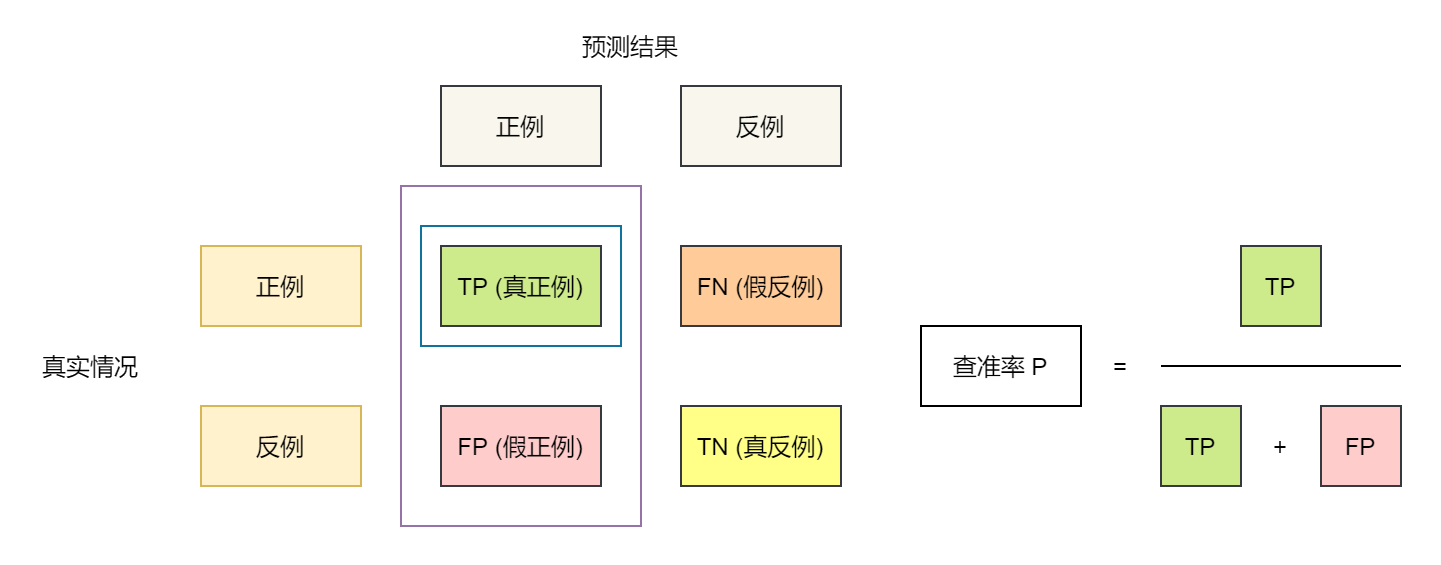
查准率 Precision
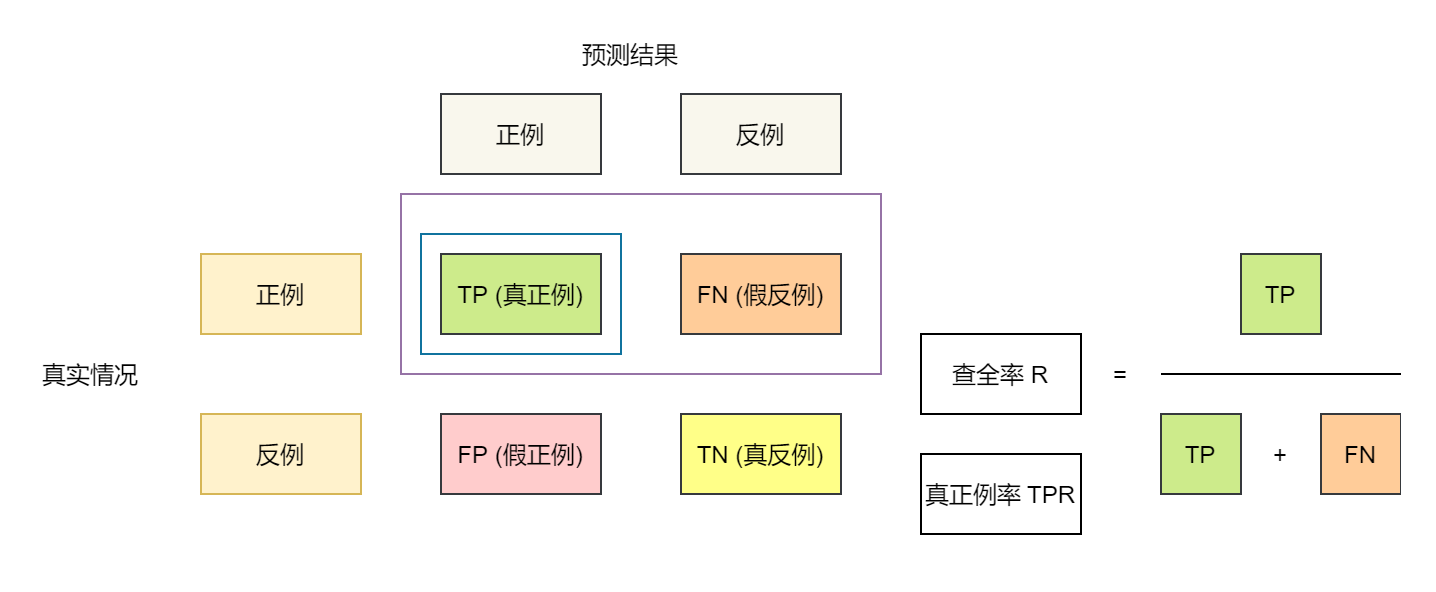
查全率 Recall 或 真正例率 Ture Positive Rate (TPR)。 在所有实际为阳性的样本中,被正确地判断为阳性之比率。
假正例率 False Positive Rate (FPR)。 在所有实际为阴性的样本中,被错误地判断为阳性之比率。
类似本文使用的逻辑回归模型,很多学习器是为测试样本产生一个实值或概率预测,然后将这个预测值与一个分类阈值(threshold)进行比较,若大于阈值则分类为正类,否则为反类。
在逻辑回归模型中,模型输出的结果是样本为正类的概率([0, 1])。
这个实值或概率预测结果的好坏,直接决定了学习器的泛化能力。 实际上,根据这个实值或概率预测结果,我们可将测试样本进行排序。
在下面的图示中,我们将“最可能”的结果(概率值最大)排在最右边,将“最不可能”的结果(概率值最小)排在最左边。 这样,分类过程就相当于在这个排序中以某个“截断点”(threshold)将样本分为两个部分,前一部分判作反例,后一部分判作正例。
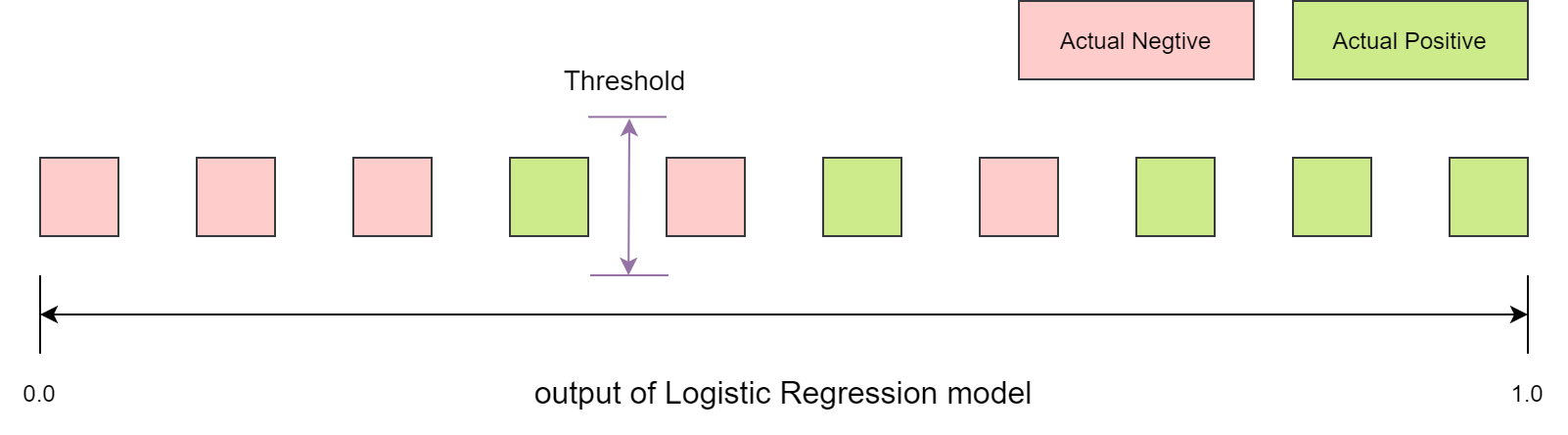
显然可以看到,在上例中,无论我们将截断点选在哪个位置,都不可能获得完全准确的预测结果。
在不同的应用任务中,我们可根据任务需求来采用不同的截断点。
- 若更重视“查准率”,则可选择上图中靠右的位置进行截断;
- 若更重视“查全率”,则可选择上图中靠左的位置进行截断。
因此,排序本身的质量好坏,体现了综合考虑学习器在不同任务下的“期望泛化性能”的好坏,或者说,“一般情况下”泛化性能的好坏。 ROC 曲线则是从这个角度出发来研究机器学习器泛化性能的有力工具。
ROC 全称是“受试者工作特性”(Receiver Operating Characteristic)曲线。
ROC 曲线的纵轴是“真正例率”(True Positive Rate,简称 TPR),横轴是“假正例率”(False Positive Rate,简称 FPR)
我们根据学习器的预测结果对样例进行排序,按此顺序逐个把样本作为正例进行预测,每次计算 FPR 和 TPR,分别以它们为横、纵坐标作图,就得到了“ROC 曲线”。
ROC 曲线数据
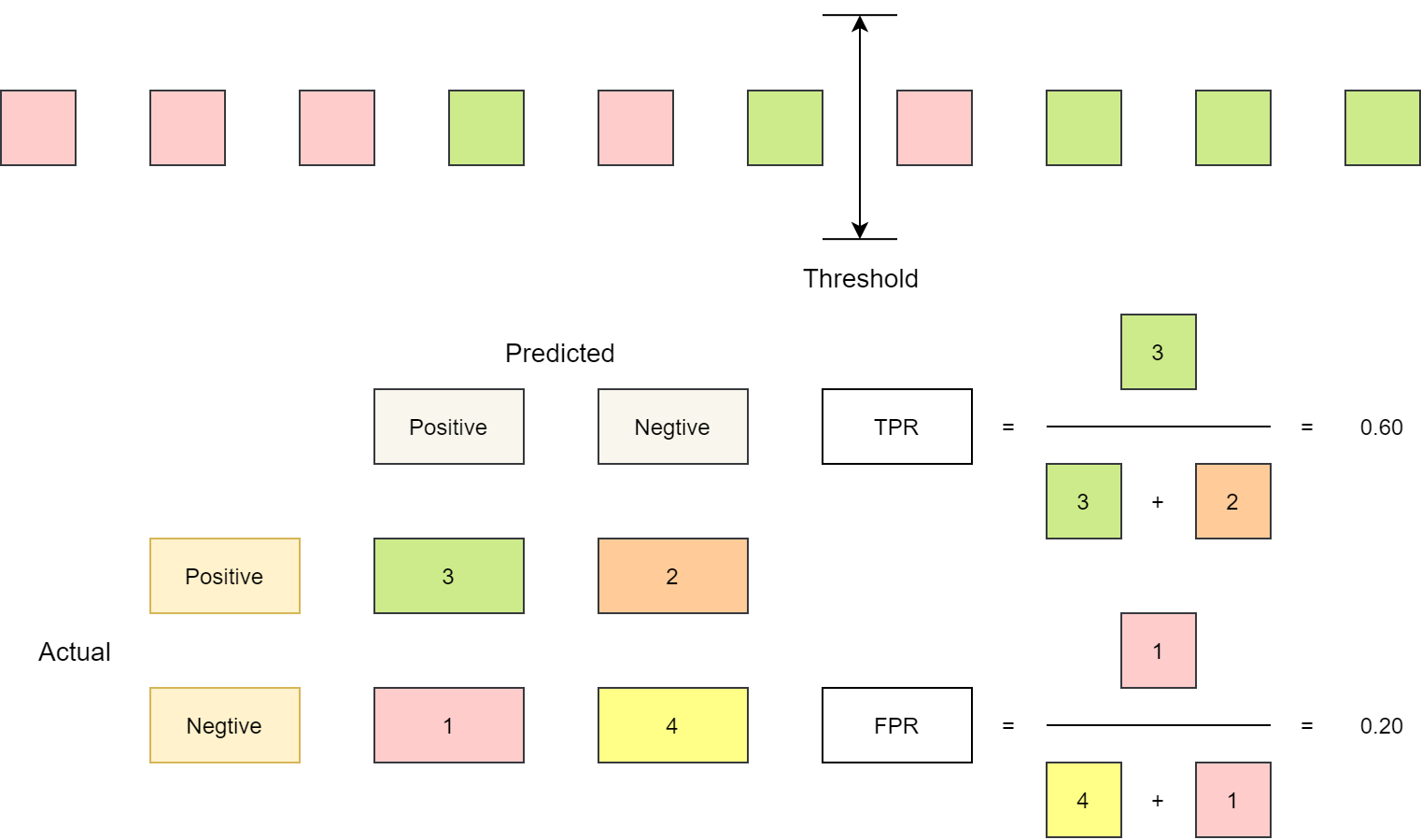
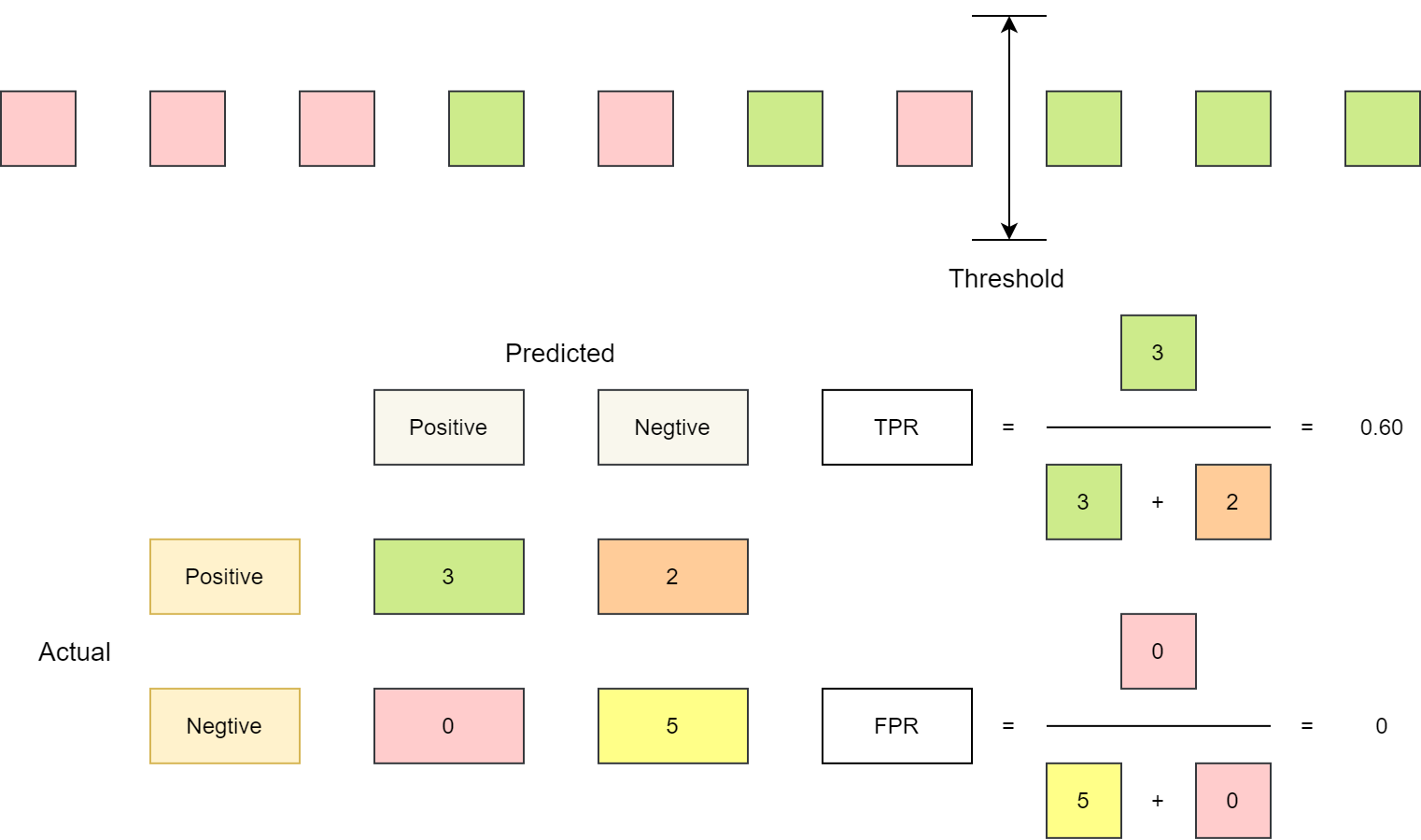
下图展示了对 10 个样本求 ROC 曲线数据的过程,10 个样本对应 11 个截断点位置,也就能得到 11 组 FPR 和 TPR。 与上面的介绍不同,下图中逐个把样本作为反例进行预测,不影响最终的绘图结果。

Round 4 计算示意图,阈值较小,所有正例均被正确分类
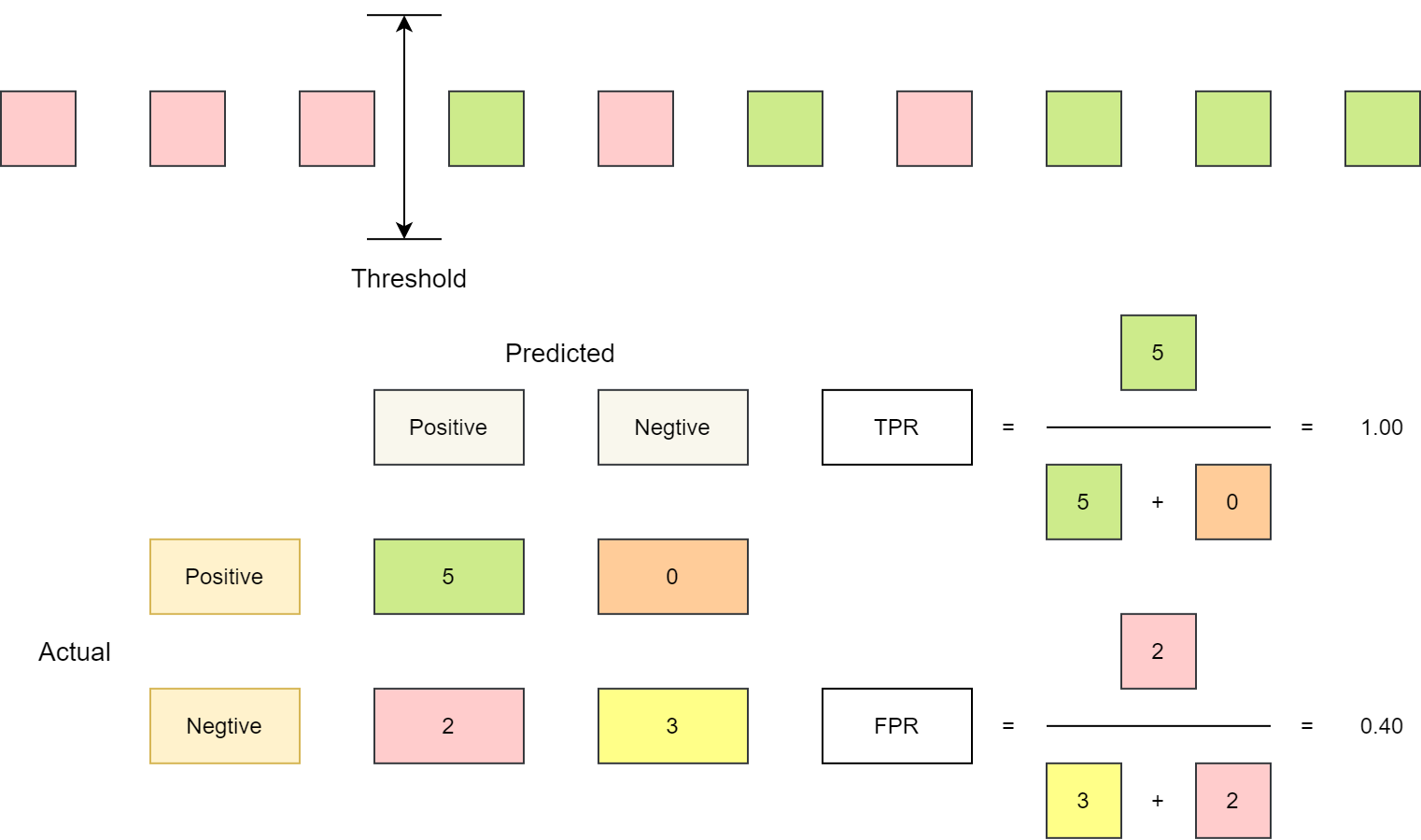
Round 5 计算示意图
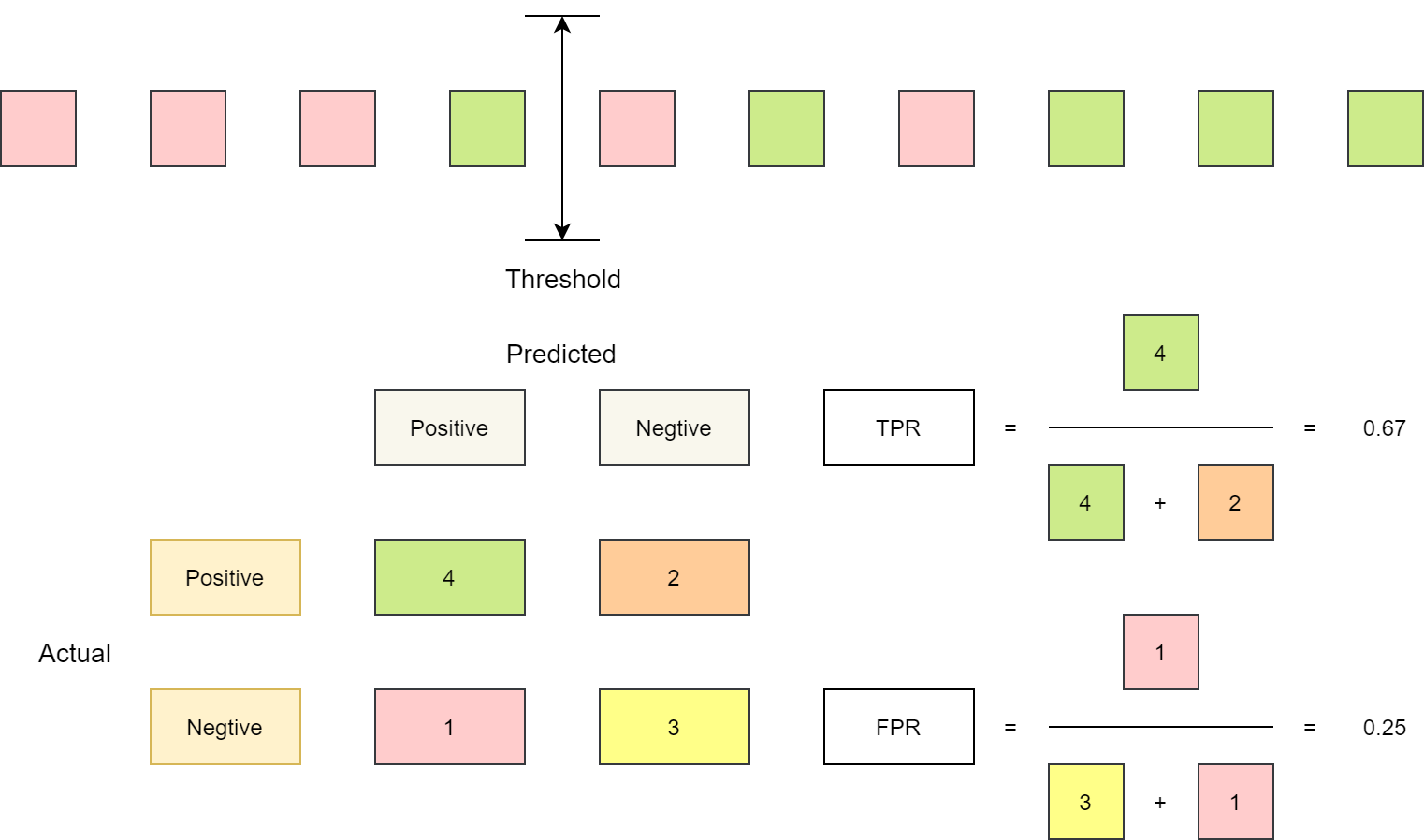
Round 7 计算示意图
Round 8 计算示意图,阈值较大,所有反例均被正确分类
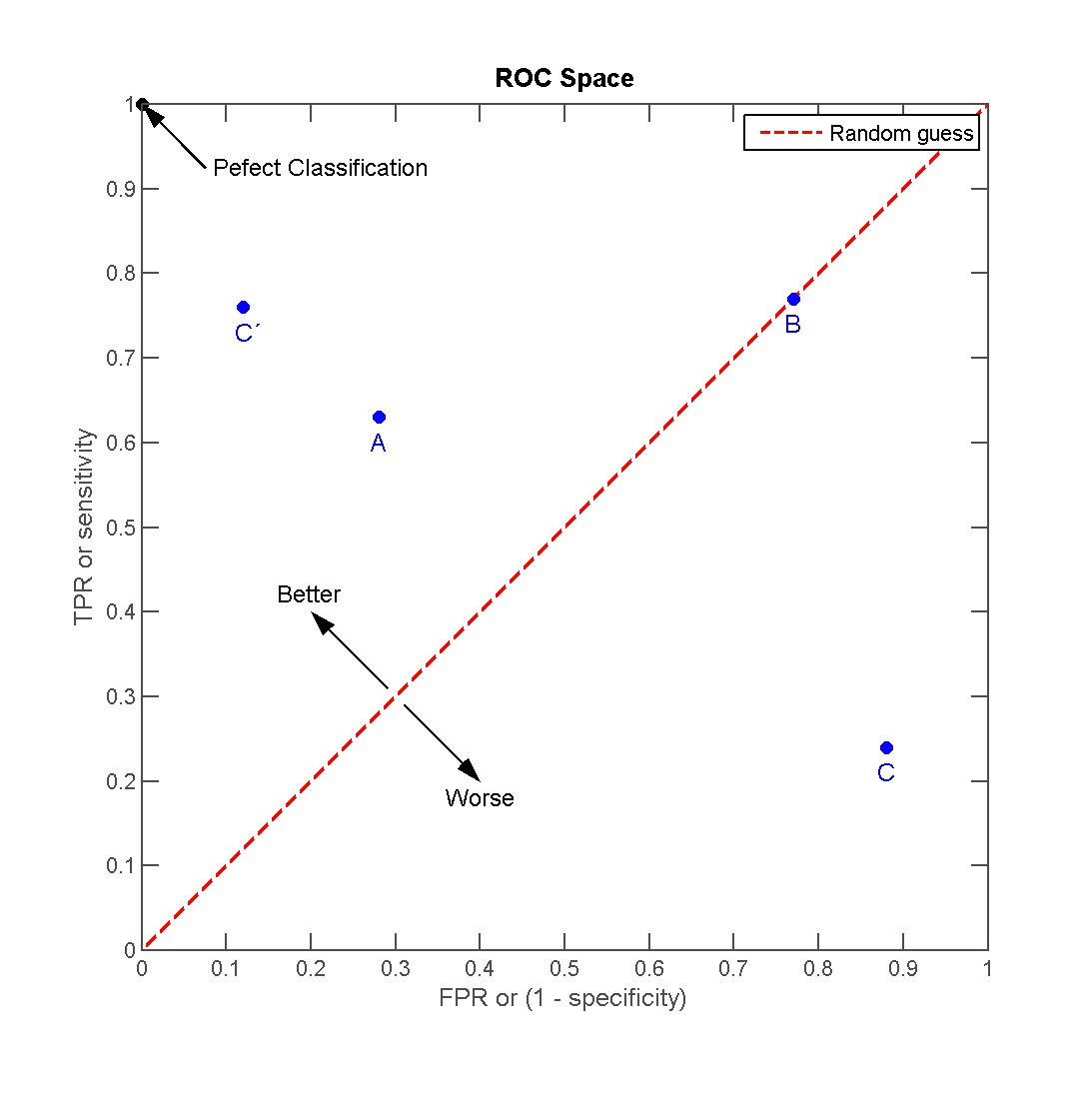
ROC 空间
从 (0, 0) 到 (1,1) 的对角线将 ROC 空间划分为左上/右下两个区域。 在这条线的以上的点代表了一个好的分类结果(胜过随机分类),而在这条线以下的点代表了差的分类结果(劣于随机分类)。
完美的预测是一个在左上角的点,在ROC空间座标 (0,1) 点,X=0 代表着没有伪阳性,Y=1 代表着没有伪阴性(所有的阳性都是真阳性); 也就是说,不管分类器输出结果是阳性或阴性,都是 100% 正确。 一个随机的预测会得到位于从 (0, 0) 到 (1, 1) 对角线(也叫无识别率线)上的一个点; 最直观的随机预测的例子就是抛硬币。
由ROC_space.png: Indonderivative work: Kai walz (talk) - ROC_space.png,CC BY-SA 3.0,https://commons.wikimedia.org/w/index.php?curid=8326140
上图将 4 种预测结果画在 ROC 空间里:
- 点与随机猜测线的距离,是预测力的指标:离左上角越近的点预测(诊断)准确率越高。离右下角越近的点,预测越不准。
- 在 A、B、C 三者当中,最好的结果是 A 方法。
- B方法的结果位于随机猜测线(对角线)上,在本例 B 的准确度(ACC)是 50%。
- C 虽然预测准确度最差,甚至劣于随机分类,也就是低于0.5(低于对角线)。然而,当将 C 以 (0.5, 0.5) 为中点作一个镜像后,C’ 的结果甚至要比 A 还要好。这个作镜像的方法,简单说,不管 C(或任何 ROC 点低于对角线的情况)预测了什么,就做相反的结论。
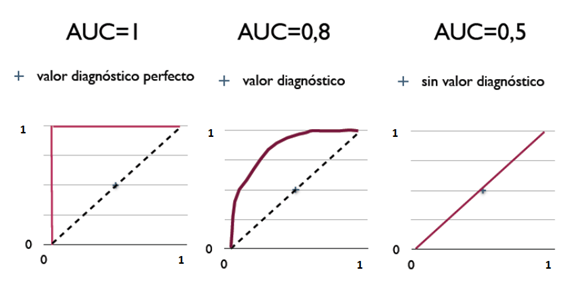
曲线下面积(AUC)
进行学习器的比较时,若一个学习器的 ROC 曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者; 若两个学习器的 ROC 曲线发生交叉,则难以一般性地断言两者孰优孰劣。 此时如果一定要进行比较,则较为合理的判据是比较 ROC 曲线下的面积,即 AUC (Area Under ROC Curve)。
由UPO649 1112 prodgom - 自己的作品,CC BY-SA 3.0,https://commons.wikimedia.org/w/index.php?curid=17086504
从AUC判断分类器(预测模型)优劣的标准:
- AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
Peirce’s skill score
又称为 Hanssen and Kuipers discriminant 或 true skill statistic,简称 TSS 和 PSS。
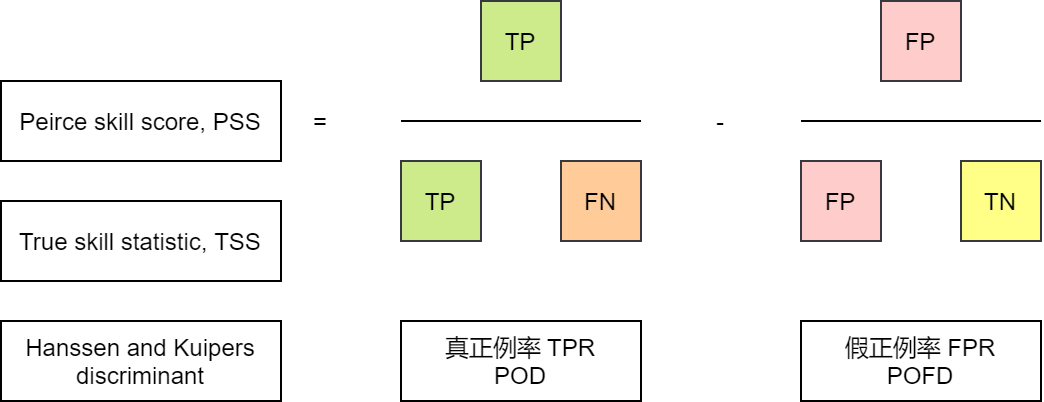
TSS 用于回答如下的问题:预测能多好地将“是”事件与“否”事件分开?
范围从 -1 到 1 之间,其中 0 说明没有技巧。完美分数是 1。
特点:使用混淆矩阵中的所有元素。 不取决于气候事件发生的频率。 该表达式与 TSS = POD - POFD 相同,但是 TSS 也可以解释为 (accuracy for events) + (accuracy for non-events) -1。 对于罕见事件,TSS 偏重于第一项(与 POD 相同),因此此分数可能对于更频繁的事件更有用。
计算 ROC 数据
get_points_in_roc_curve 返回 :
- POFD(probability of false detection,假阳率)
- POD(probability of detection,真阳率)
def get_points_in_roc_curve(
observed_labels: np.ndarray,
forecast_probabilities: np.ndarray,
) -> (np.ndarray, np.ndarray):
# 观察标签必须是 0 或 1
assert np.all(np.logical_or(
observed_labels == 0, observed_labels == 1
))
# 预报概率必须在 [0, 1] 之间
assert np.all(np.logical_and(
forecast_probabilities >= 0, forecast_probabilities <= 1
))
observed_labels = observed_labels.astype(int)
# 将 [0, 1] 分成 1000 等份,一共 1001 个阈值
binarization_thresholds = np.linspace(
0, 1,
num=1001,
dtype=float
)
num_thresholds = len(binarization_thresholds)
pofd_by_threshold = np.full(num_thresholds, np.nan)
pod_by_threshold = np.full(num_thresholds, np.nan)
# 针对每个阈值,计算 FPR 和 TPR
for k in range(num_thresholds):
# 预测结果大于某阈值的标签,即按某阈值分类的结果
these_forecast_labels = (
forecast_probabilities >= binarization_thresholds[k]
).astype(int)
# 真正例 TP
this_num_hits = np.sum(np.logical_and(
these_forecast_labels == 1, observed_labels == 1
))
# 假正例 FP
this_num_false_alarms = np.sum(np.logical_and(
these_forecast_labels == 1, observed_labels == 0
))
# 假反例 FN
this_num_misses = np.sum(np.logical_and(
these_forecast_labels == 0, observed_labels == 1
))
# 真反例 TN
this_num_correct_nulls = np.sum(np.logical_and(
these_forecast_labels == 0, observed_labels == 0
))
try:
# 假正例率 FPR = FP / (FP + TN)
pofd_by_threshold[k] = (
float(this_num_false_alarms) /
(this_num_false_alarms + this_num_correct_nulls)
)
except ZeroDivisionError:
pass
try:
# 真正例率 TPR = TP / (TP + FN)
pod_by_threshold[k] = (
float(this_num_hits) / (this_num_hits + this_num_misses)
)
except ZeroDivisionError:
pass
pod_by_threshold = np.array([1.] + pod_by_threshold.tolist() + [0.])
pofd_by_threshold = np.array([1.] + pofd_by_threshold.tolist() + [0.])
return pofd_by_threshold, pod_by_threshold使用示例
pofd_by_threshold, pod_by_threshold = get_points_in_roc_curve(
observed_labels=training_target_table["strong_future_rotation_flag"].values,
forecast_probabilities=training_probabilities,
)
pofd_by_threshold.shape(1003,)
pofd_by_threshold[:10], pod_by_threshold[:10](array([1. , 1. , 0.9971039 , 0.97750062, 0.94379521,
0.90431214, 0.86481452, 0.82584082, 0.79018526, 0.75739671]),
array([1. , 1. , 1. , 0.99973904, 0.9993476 ,
0.99843424, 0.99765136, 0.99634656, 0.99543319, 0.99412839]))
pofd_by_threshold[-10:], pod_by_threshold[-10:](array([2.61959163e-04, 2.18299303e-04, 1.45532869e-04, 8.73197212e-05,
4.36598606e-05, 4.36598606e-05, 2.91065737e-05, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00]),
array([0.01918058, 0.01748434, 0.01526618, 0.01291754, 0.01004697,
0.00691545, 0.00391441, 0.00247912, 0. , 0. ]))
绘制 ROC 曲线
plot_roc_curve 函数用于绘制 ROC 曲线
def plot_roc_curve(
observed_labels,
forecast_probabilities,
line_colour=np.array([228, 26, 28], dtype=float) / 255,
line_width=3,
random_line_colour=np.full(3, 152. / 255),
random_line_width=2,
axes_object=None
) -> (np.ndarray, np.ndarray):
pofd_by_threshold, pod_by_threshold = get_points_in_roc_curve(
observed_labels=observed_labels,
forecast_probabilities=forecast_probabilities
)
if axes_object is None:
_, axes_object = pyplot.subplots(
1, 1, figsize=(10, 10)
)
# POFD 和 POD 坐标网格
pofd_matrix, pod_matrix = _get_pofd_pod_grid()
# 计算每个点的 Peirce 评分
peirce_score_matrix = pod_matrix - pofd_matrix
colour_map_object, colour_norm_object = _get_peirce_colour_scheme()
# 绘制 Peirce 的填充图,忽略 Peirce 评分小于 0 的值
pyplot.contourf(
pofd_matrix,
pod_matrix,
peirce_score_matrix,
LEVELS_FOR_PEIRCE_CONTOURS,
cmap=colour_map_object,
norm=colour_norm_object,
vmin=0.,
vmax=1.,
axes=axes_object
)
colour_bar_object = _add_colour_bar(
axes_object=axes_object,
colour_map_object=colour_map_object,
colour_norm_object=colour_norm_object,
values_to_colour=peirce_score_matrix,
min_colour_value=0.,
max_colour_value=1.,
orientation_string='vertical',
extend_min=False,
extend_max=False
)
print(colour_bar_object)
colour_bar_object.set_label('Peirce score')
# 绘制随机猜想线(虚线),Peirce 评分 = 0
random_x_coords = np.array([0., 1.])
random_y_coords = np.array([0., 1.])
axes_object.plot(
random_x_coords,
random_y_coords,
color=random_line_colour,
linestyle='dashed',
linewidth=random_line_width
)
nan_flags = np.logical_or(
np.isnan(pofd_by_threshold),
np.isnan(pod_by_threshold)
)
if not np.all(nan_flags):
real_indices = np.where(np.invert(nan_flags))[0]
# 绘制 ROC 曲线
axes_object.plot(
pofd_by_threshold[real_indices],
pod_by_threshold[real_indices],
color=line_colour,
linestyle='solid',
linewidth=line_width
)
axes_object.set_xlabel('POFD (probability of false detection)')
axes_object.set_ylabel('POD (probability of detection)')
axes_object.set_xlim(0., 1.)
axes_object.set_ylim(0., 1.)
return pofd_by_threshold, pod_by_threshold_get_pofd_pod_grid 返回 POFD-POD 空间的坐标网格:
- x 轴:POFD
- y 轴:POD
范围均是 0 - 1 之间
def _get_pofd_pod_grid(
pofd_spacing=0.01,
pod_spacing=0.01
):
num_pofd_values = 1 + int(np.ceil(1. / pofd_spacing))
num_pod_values = 1 + int(np.ceil(1. / pod_spacing))
unique_pofd_values = np.linspace(0., 1., num=num_pofd_values)
unique_pod_values = np.linspace(0., 1., num=num_pod_values)[::-1]
return np.meshgrid(unique_pofd_values, unique_pod_values)pofd_grid, pod_grid = _get_pofd_pod_grid()
pofd_grid, pod_grid(array([[0. , 0.01, 0.02, ..., 0.98, 0.99, 1. ],
[0. , 0.01, 0.02, ..., 0.98, 0.99, 1. ],
[0. , 0.01, 0.02, ..., 0.98, 0.99, 1. ],
...,
[0. , 0.01, 0.02, ..., 0.98, 0.99, 1. ],
[0. , 0.01, 0.02, ..., 0.98, 0.99, 1. ],
[0. , 0.01, 0.02, ..., 0.98, 0.99, 1. ]]),
array([[1. , 1. , 1. , ..., 1. , 1. , 1. ],
[0.99, 0.99, 0.99, ..., 0.99, 0.99, 0.99],
[0.98, 0.98, 0.98, ..., 0.98, 0.98, 0.98],
...,
[0.02, 0.02, 0.02, ..., 0.02, 0.02, 0.02],
[0.01, 0.01, 0.01, ..., 0.01, 0.01, 0.01],
[0. , 0. , 0. , ..., 0. , 0. , 0. ]]))
_get_peirce_colour_scheme 函数为 Peirce score 返回色表
def _get_peirce_colour_scheme() -> (
matplotlib.colors.ListedColormap,
matplotlib.colors.BoundaryNorm
):
LEVELS_FOR_PEIRCE_CONTOURS = np.linspace(0, 1, num=11, dtype=float)
this_colour_map_object = pyplot.cm.Blues
# 创建离散色表的规范化器
this_colour_norm_object = matplotlib.colors.BoundaryNorm(
LEVELS_FOR_PEIRCE_CONTOURS,
this_colour_map_object.N # 色表颜色的个数
)
# RGBA 颜色矩阵
rgba_matrix = this_colour_map_object(
this_colour_norm_object(
LEVELS_FOR_PEIRCE_CONTOURS
)
)
# 删掉最后一个通道
colour_list = [
rgba_matrix[i, ..., :-1] for i in range(rgba_matrix.shape[0])
]
# 色表对象
colour_map_object = matplotlib.colors.ListedColormap(colour_list)
# 将低于范围外的值的颜色设为 [1,1,1]
colour_map_object.set_under(
np.array([1, 1, 1])
)
colour_norm_object = matplotlib.colors.BoundaryNorm(
LEVELS_FOR_PEIRCE_CONTOURS,
colour_map_object.N
)
return colour_map_object, colour_norm_object使用该函数返回的两个对象,绘制色表
scalar_mappable_object = pyplot.cm.ScalarMappable(
cmap=colour_map_object,
norm=colour_norm_object
)
pyplot.colorbar(
mappable=scalar_mappable_object,
orientation='horizontal',
pad=0.075,
extend='both',
shrink=1
)
pyplot.gca().set_visible(False)
_add_colour_bar 在现有绘图中添加颜色条
def _add_colour_bar(
axes_object,
colour_map_object,
values_to_colour,
min_colour_value: float,
max_colour_value: float,
colour_norm_object=None,
orientation_string='vertical',
extend_min=True,
extend_max=True,
fraction_of_axis_length=1.,
font_size=FONT_SIZE
):
if colour_norm_object is None:
colour_norm_object = matplotlib.colors.Normalize(
vmin=min_colour_value,
vmax=max_colour_value,
clip=False
)
scalar_mappable_object = pyplot.cm.ScalarMappable(
cmap=colour_map_object,
norm=colour_norm_object
)
scalar_mappable_object.set_array(values_to_colour)
if extend_min and extend_max:
extend_string = 'both'
elif extend_min:
extend_string = 'min'
elif extend_max:
extend_string = 'max'
else:
extend_string = 'neither'
if orientation_string == 'horizontal':
padding = 0.075
else:
padding = 0.05
colour_bar_object = pyplot.colorbar(
ax=axes_object,
mappable=scalar_mappable_object,
orientation=orientation_string,
pad=padding,
extend=extend_string,
shrink=fraction_of_axis_length
)
colour_bar_object.ax.tick_params(labelsize=font_size)
return colour_bar_object绘图示例
_, axes_object = pyplot.subplots(
1, 1,
figsize=(10, 10)
)
pofd_by_threshold, pod_by_threshold = plot_roc_curve(
observed_labels=training_target_table["strong_future_rotation_flag"].values,
forecast_probabilities=training_probabilities,
axes_object=axes_object
)
# 计算 AUC (Area Under ROC Curve,ROC 曲线下面积)
area_under_roc_curve = sklearn.metrics.auc(
x=pofd_by_threshold,
y=pod_by_threshold,
)
pyplot.title(
f'training ROC curve '
f'(AUC = {area_under_roc_curve:.3f})'
)
pyplot.show()
详细分析
获取 POFD 和 POD 数据
pofd_by_threshold, pod_by_threshold = get_points_in_roc_curve(
observed_labels=training_target_table["strong_future_rotation_flag"].values,
forecast_probabilities=training_probabilities
)获取坐标网格
pofd_matrix, pod_matrix = _get_pofd_pod_grid()
pofd_matrix, pod_matrix(array([[0. , 0.01, 0.02, ..., 0.98, 0.99, 1. ],
[0. , 0.01, 0.02, ..., 0.98, 0.99, 1. ],
[0. , 0.01, 0.02, ..., 0.98, 0.99, 1. ],
...,
[0. , 0.01, 0.02, ..., 0.98, 0.99, 1. ],
[0. , 0.01, 0.02, ..., 0.98, 0.99, 1. ],
[0. , 0.01, 0.02, ..., 0.98, 0.99, 1. ]]),
array([[1. , 1. , 1. , ..., 1. , 1. , 1. ],
[0.99, 0.99, 0.99, ..., 0.99, 0.99, 0.99],
[0.98, 0.98, 0.98, ..., 0.98, 0.98, 0.98],
...,
[0.02, 0.02, 0.02, ..., 0.02, 0.02, 0.02],
[0.01, 0.01, 0.01, ..., 0.01, 0.01, 0.01],
[0. , 0. , 0. , ..., 0. , 0. , 0. ]]))
计算每个点的 Peirce 评分
peirce_score_matrix = pod_matrix - pofd_matrix
peirce_score_matrixarray([[ 1. , 0.99, 0.98, ..., 0.02, 0.01, 0. ],
[ 0.99, 0.98, 0.97, ..., 0.01, 0. , -0.01],
[ 0.98, 0.97, 0.96, ..., 0. , -0.01, -0.02],
...,
[ 0.02, 0.01, 0. , ..., -0.96, -0.97, -0.98],
[ 0.01, 0. , -0.01, ..., -0.97, -0.98, -0.99],
[ 0. , -0.01, -0.02, ..., -0.98, -0.99, -1. ]])
为 Peirce 评分创建色表
colour_map_object, colour_norm_object = _get_peirce_colour_scheme()绘制 Peirce 的填充图,忽略 Peirce 评分小于 0 的值
绘制随机猜想线(虚线),Peirce 评分 = 0
_, axes_object = pyplot.subplots(
1, 1,
figsize=(10, 10)
)
pyplot.contourf(
pofd_matrix,
pod_matrix,
peirce_score_matrix,
LEVELS_FOR_PEIRCE_CONTOURS,
cmap=colour_map_object,
norm=colour_norm_object,
vmin=0.,
vmax=1.,
axes=axes_object
)
colour_bar_object = _add_colour_bar(
axes_object=axes_object,
colour_map_object=colour_map_object,
colour_norm_object=colour_norm_object,
values_to_colour=peirce_score_matrix,
min_colour_value=0.,
max_colour_value=1.,
orientation_string='vertical',
extend_min=False,
extend_max=False
)
colour_bar_object.set_label('Peirce score')
random_x_coords = np.array([0., 1.])
random_y_coords = np.array([0., 1.])
random_line_colour=np.full(3, 152. / 255)
random_line_width=2
axes_object.plot(
random_x_coords,
random_y_coords,
color=random_line_colour,
linestyle='dashed',
linewidth=random_line_width
)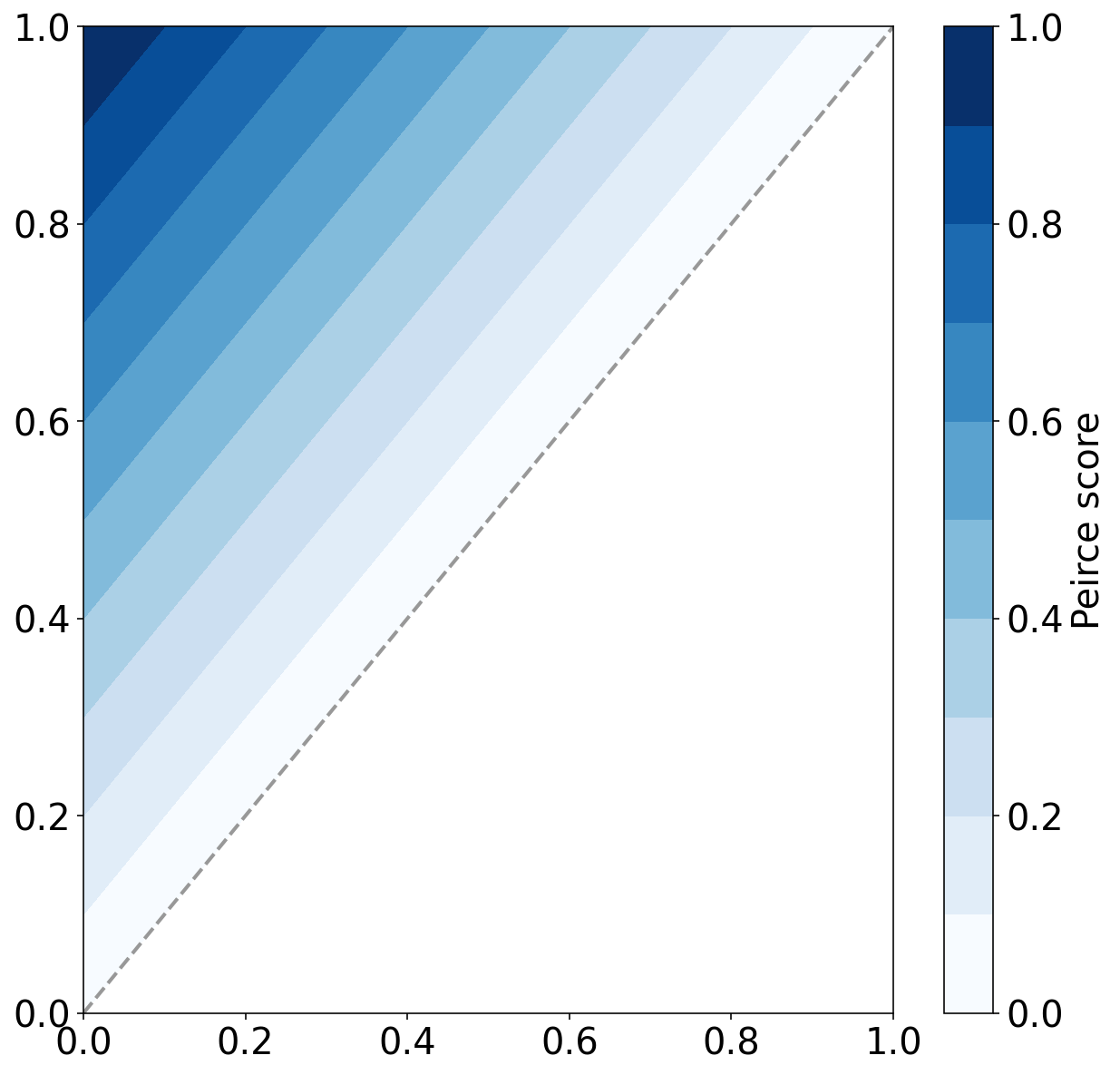
最后再绘制由实际计算的 ROC 数据构成的折线,不再介绍。
参考
https://github.com/djgagne/ams-ml-python-course
https://www.cawcr.gov.au/projects/verification/
https://developers.google.com/machine-learning/crash-course/classification/roc-and-auc
AMS 机器学习课程
数据预处理:
实际数据处理:
《AMS机器学习课程:预测雷暴旋转的基础机器学习 - 数据》
线性回归:
《AMS机器学习课程:预测雷暴旋转的基础机器学习 - 线性回归》
《AMS机器学习课程:预测雷暴旋转的基础机器学习 - 正则化》
《AMS机器学习课程:预测雷暴旋转的基础机器学习 - 超参数试验》
逻辑回归:
