ISLR实验：岭回归和lasso
目录
本文源自《统计学习导论：基于R语言应用》(ISLR) 中《6.6 实验2：岭回归和lasso》章节
介绍两种压缩估计方法
使用对系数进行约束或加罚的技巧对包含 p 个预测变量的模型进行拟合，也就是说，将系数估计值往零的方向压缩。
library(ISLR)
library(glmnet)
数据
棒球数据集，使用若干与棒球运动员上一年比赛成绩相关的变量来预测该运动员的薪水 (Salary)
head(Hitters)
AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits
-Andy Allanson 293 66 1 30 29 14 1 293 66
-Alan Ashby 315 81 7 24 38 39 14 3449 835
-Alvin Davis 479 130 18 66 72 76 3 1624 457
-Andre Dawson 496 141 20 65 78 37 11 5628 1575
-Andres Galarraga 321 87 10 39 42 30 2 396 101
-Alfredo Griffin 594 169 4 74 51 35 11 4408 1133
CHmRun CRuns CRBI CWalks League Division PutOuts
-Andy Allanson 1 30 29 14 A E 446
-Alan Ashby 69 321 414 375 N W 632
-Alvin Davis 63 224 266 263 A W 880
-Andre Dawson 225 828 838 354 N E 200
-Andres Galarraga 12 48 46 33 N E 805
-Alfredo Griffin 19 501 336 194 A W 282
Assists Errors Salary NewLeague
-Andy Allanson 33 20 NA A
-Alan Ashby 43 10 475.0 N
-Alvin Davis 82 14 480.0 A
-Andre Dawson 11 3 500.0 N
-Andres Galarraga 40 4 91.5 N
-Alfredo Griffin 421 25 750.0 A
dim(Hitters)
[1] 322 20
names(Hitters)
[1] "AtBat" "Hits" "HmRun" "Runs" "RBI"
[6] "Walks" "Years" "CAtBat" "CHits" "CHmRun"
[11] "CRuns" "CRBI" "CWalks" "League" "Division"
[16] "PutOuts" "Assists" "Errors" "Salary" "NewLeague"
处理缺失值
sum(is.na(Hitters))
[1] 59
删掉缺失值条目
hitters <- na.omit(Hitters)
dim(hitters)
[1] 263 20
sum(is.na(hitters))
[1] 0
构造数据集
x <- model.matrix(Salary ~ ., hitters)[, -1]
y <- hitters$Salary
岭回归
ridge regression
最小化函数
最小二乘回归：
$$ RSS = \sum_{i=1}^n(y_i - \beta_0 - \sum_{j=1}^p\beta_jx_{ij})^2 $$
岭回归：
$$ \sum_{i=1}^n(y_i - \beta_0 - \sum_{j=1}^p\beta_jx_{ij})^2 + \lambda\sum_{j=1}^p\beta_j^2 = RSS + \lambda\sum_{j=1}^p\beta_j^2 $$
其中 lambda 是调节参数，增加的项是压缩惩罚，使用 L2 范数
拟合岭回归模型
glmnet 包的 glmnet() 函数使用参数 alpha 选择模型：
alpha=0：岭回归alpha=1：lasso
设置参数 lambda 范围
grid <- 10^seq(10, -2, length=100)
拟合模型
注：glmnet() 默认对所有变量进行标准化
ridge_model <- glmnet(
x, y,
alpha=0,
lambda=grid
)
系数矩阵
每个 labmda 取值对应一个系数向量
coef() 函数返回的系数矩阵中每行对应一个预测变量，每列对应一个 lambda 取值
dim(coef(ridge_model))
[1] 20 100
比较系数大小
使用 L2 范数时，一般认为较大 lambda 值对应的系数值远小于较小 lambda 值对应的系数
较大 lambda 值
ridge_model$lambda[50]
[1] 11497.57
coef(ridge_model)[, 50]
(Intercept) AtBat Hits HmRun Runs
407.356050200 0.036957182 0.138180344 0.524629976 0.230701523
RBI Walks Years CAtBat CHits
0.239841459 0.289618741 1.107702929 0.003131815 0.011653637
CHmRun CRuns CRBI CWalks LeagueN
0.087545670 0.023379882 0.024138320 0.025015421 0.085028114
DivisionW PutOuts Assists Errors NewLeagueN
-6.215440973 0.016482577 0.002612988 -0.020502690 0.301433531
较小 lambda 值
ridge_model$lambda[60]
[1] 705.4802
coef(ridge_model)[, 60]
(Intercept) AtBat Hits HmRun Runs
54.32519950 0.11211115 0.65622409 1.17980910 0.93769713
RBI Walks Years CAtBat CHits
0.84718546 1.31987948 2.59640425 0.01083413 0.04674557
CHmRun CRuns CRBI CWalks LeagueN
0.33777318 0.09355528 0.09780402 0.07189612 13.68370191
DivisionW PutOuts Assists Errors NewLeagueN
-54.65877750 0.11852289 0.01606037 -0.70358655 8.61181213
预测
获取新 lambda 值对应的岭回归系数
predict(
ridge_model,
s=50,
type="coefficients"
)[1:20,]
(Intercept) AtBat Hits HmRun Runs
4.876610e+01 -3.580999e-01 1.969359e+00 -1.278248e+00 1.145892e+00
RBI Walks Years CAtBat CHits
8.038292e-01 2.716186e+00 -6.218319e+00 5.447837e-03 1.064895e-01
CHmRun CRuns CRBI CWalks LeagueN
6.244860e-01 2.214985e-01 2.186914e-01 -1.500245e-01 4.592589e+01
DivisionW PutOuts Assists Errors NewLeagueN
-1.182011e+02 2.502322e-01 1.215665e-01 -3.278600e+00 -9.496680e+00
测试误差
训练集和测试集
分割数据集的常用方法：
- 生成与数据集大小相同的 TRUE/FALSE 向量
- 生成 1..n 数字子集，作为训练集的索引
set.seed(1)
train <- sample(1:nrow(x), nrow(x)/2)
test <- (-train)
y_test <- y[test]
拟合
使用训练集拟合
ridge_model <- glmnet(
x[train,],
y[train],
alpha=0,
lambda=grid,
thresh=1e-12
)
计算 lambda = 4 时测试集的 MSE
ridge_predict <- predict(
ridge_model,
s=4,
newx=x[test,]
)
mean((ridge_predict - y_test)^2)
[1] 142199.2
计算 lambda = 1e10 时测试集的 MSE
ridge_predict <- predict(
ridge_model,
s=1e10,
newx=x[test,]
)
mean((ridge_predict - y_test)^2)
[1] 224669.8
计算最小二乘回归模型的 MSE，即 lambda = 0
ridge_lm <- glmnet(
x[train,],
y[train],
alpha=0,
lambda=0,
thresh=1e-12
)
ridge_predict <- predict(
ridge_lm,
s=0,
newx=x[test,],
exact=TRUE
)
mean((ridge_predict - y_test)^2)
[1] 168588.6
对比系数
线性回归
lm(y ~ x, subset=train)
Call:
lm(formula = y ~ x, subset = train)
Coefficients:
(Intercept) xAtBat xHits xHmRun xRuns
274.0145 -0.3521 -1.6377 5.8145 1.5424
xRBI xWalks xYears xCAtBat xCHits
1.1243 3.7287 -16.3773 -0.6412 3.1632
xCHmRun xCRuns xCRBI xCWalks xLeagueN
3.4008 -0.9739 -0.6005 0.3379 119.1486
xDivisionW xPutOuts xAssists xErrors xNewLeagueN
-144.0831 0.1976 0.6804 -4.7128 -71.0951
lambda = 0 时的岭回归
predict(
ridge_lm,
s=0,
exact=TRUE,
type="coefficients"
)[1:20,]
(Intercept) AtBat Hits HmRun Runs
274.0200971 -0.3521900 -1.6371383 5.8146698 1.5423360
RBI Walks Years CAtBat CHits
1.1241836 3.7288406 -16.3795188 -0.6411235 3.1629444
CHmRun CRuns CRBI CWalks LeagueN
3.4005278 -0.9739405 -0.6003975 0.3378422 119.1434633
DivisionW PutOuts Assists Errors NewLeagueN
-144.0853061 0.1976300 0.6804200 -4.7127878 -71.0898897
交叉验证
cv.glmnet()
set.seed(1)
cv_out <- cv.glmnet(
x[train,],
y[train],
alpha=0
)
plot(cv_out)
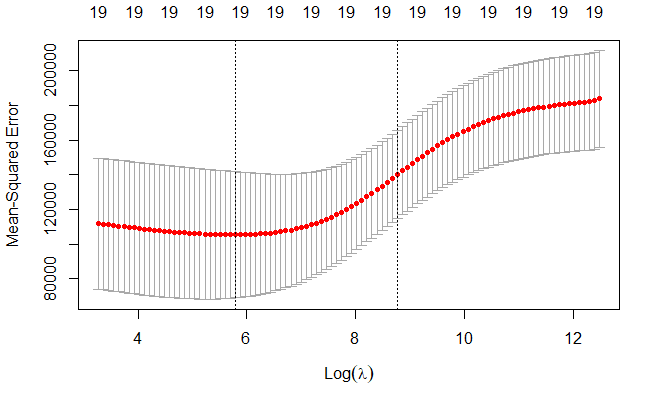
交叉验证误差最小的 lambda 值
bestlam <- cv_out$lambda.min
bestlam
[1] 326.0828
对应的测试 MSE
ridge_predict <- predict(
ridge_model,
s=bestlam,
newx=x[test,]
)
mean((ridge_predict - y_test)^2)
[1] 139856.6
在整个数据集上训练，得到变量的系数
out <- glmnet(
x, y,
alpha=0
)
predict(
out,
type="coefficients",
s=bestlam
)[1:20,]
(Intercept) AtBat Hits HmRun Runs
15.44383135 0.07715547 0.85911581 0.60103107 1.06369007
RBI Walks Years CAtBat CHits
0.87936105 1.62444616 1.35254780 0.01134999 0.05746654
CHmRun CRuns CRBI CWalks LeagueN
0.40680157 0.11456224 0.12116504 0.05299202 22.09143189
DivisionW PutOuts Assists Errors NewLeagueN
-79.04032637 0.16619903 0.02941950 -1.36092945 9.12487767
没有一个变量的系数为 0，岭回归没有筛选出变量
lasso
最小化函数
$$ \sum_{i=1}^n(y_i - \beta_0 - \sum_{j=1}^p\beta_jx_{ij})^2 + \lambda\sum_{j=1}^p|\beta_j| = RSS + \lambda\sum_{j=1}^p|\beta_j| $$
惩罚项使用 L1 范数
拟合模型
使用 alpha=1 拟合 lasso 模型
lasso_model <- glmnet(
x[train,],
y[train],
alpha=1,
lambda=grid
)
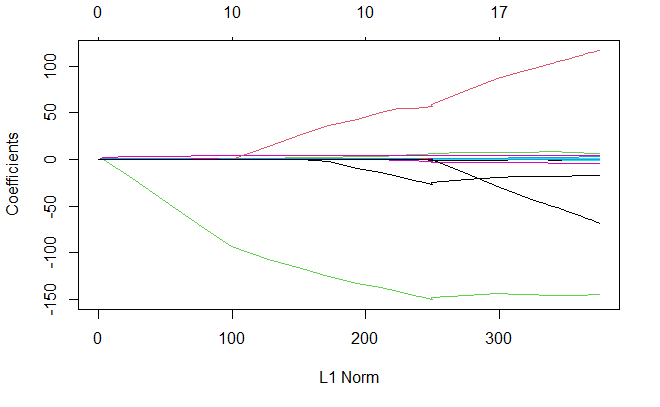
绘制系数与 lambda 值的关系
plot(lasso_model)
使用交叉验证并计算相应的测试误差
set.seed(1)
cv_out <- cv.glmnet(
x[train,],
y[train],
alpha=1
)
plot(cv_out)
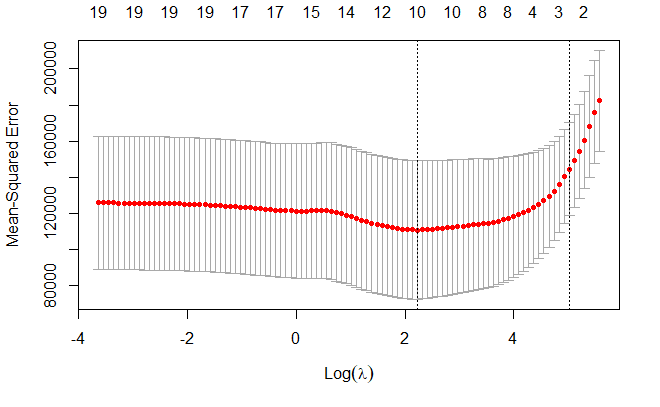
交叉验证误差最小的 lambda 值
bestlam <- cv_out$lambda.min
bestlam
[1] 9.286955
lasso_predict <- predict(
lasso_model,
s=bestlam,
newx=x[test,]
)
mean((lasso_predict - y_test)^2)
[1] 143673.6
使用全部数据重新拟合，得到变量的系数
out <- glmnet(
x, y,
alpha=1,
lambda=grid
)
lasso_coef <- predict(
out,
type="coefficients",
s=bestlam,
)[1:20,]
lasso_coef
(Intercept) AtBat Hits HmRun Runs
1.27479059 -0.05497143 2.18034583 0.00000000 0.00000000
RBI Walks Years CAtBat CHits
0.00000000 2.29192406 -0.33806109 0.00000000 0.00000000
CHmRun CRuns CRBI CWalks LeagueN
0.02825013 0.21628385 0.41712537 0.00000000 20.28615023
DivisionW PutOuts Assists Errors NewLeagueN
-116.16755870 0.23752385 0.00000000 -0.85629148 0.00000000
lasso_coef[lasso_coef!=0]
(Intercept) AtBat Hits Walks Years
1.27479059 -0.05497143 2.18034583 2.29192406 -0.33806109
CHmRun CRuns CRBI LeagueN DivisionW
0.02825013 0.21628385 0.41712537 20.28615023 -116.16755870
PutOuts Errors
0.23752385 -0.85629148
lasso 的系数估计是稀疏的，上述模型中有 8 个变量的系数为 0，模型仅包含 11 个变量
参考
https://github.com/perillaroc/islr-study
参考
https://github.com/perillaroc/islr-study
ISLR实验系列文章
线性回归
分类
重抽样方法
线性模型选择与正则化
