ISLR实验:多元线性回归
本文源自《统计学习导论:基于R语言应用》(ISLR) 中《3.6 实验:线性回归》章节
使用 Boston 数据集
library(MASS)
library(ISLR)拟合
语句 lm(y ~ x1 + x2) 建立两个预测变量 x1,x2 的拟合模型
lm.fit.2 <- lm(medv ~ lstat + age, data=Boston)summary() 函数输出预测变量的回归系数
summary(lm.fit.2)Call:
lm(formula = medv ~ lstat + age, data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.981 -3.978 -1.283 1.968 23.158
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 33.22276 0.73085 45.458 < 2e-16 ***
lstat -1.03207 0.04819 -21.416 < 2e-16 ***
age 0.03454 0.01223 2.826 0.00491 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.173 on 503 degrees of freedom
Multiple R-squared: 0.5513, Adjusted R-squared: 0.5495
F-statistic: 309 on 2 and 503 DF, p-value: < 2.2e-16
绘制诊断图
par(mfrow=c(2, 2))
plot(lm.fit.2)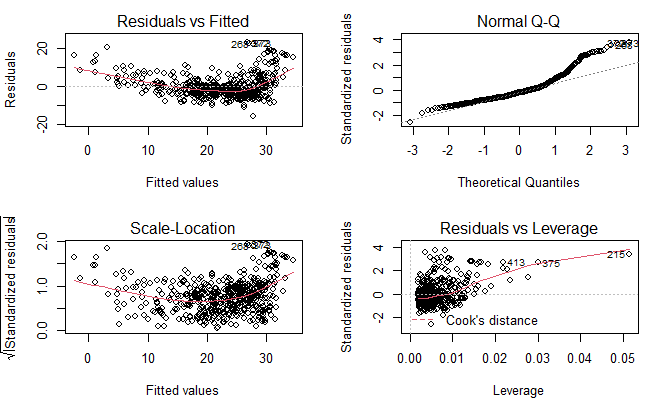
使用下面的方法对所有预测变量进行回归
lm.fit.all <- lm(medv~., data=Boston)
lm.fit.allCall:
lm(formula = medv ~ ., data = Boston)
Coefficients:
(Intercept) crim zn indus chas nox rm
3.646e+01 -1.080e-01 4.642e-02 2.056e-02 2.687e+00 -1.777e+01 3.810e+00
age dis rad tax ptratio black lstat
6.922e-04 -1.476e+00 3.060e-01 -1.233e-02 -9.527e-01 9.312e-03 -5.248e-01
summary(lm.fit.all)Residuals:
Min 1Q Median 3Q Max
-15.595 -2.730 -0.518 1.777 26.199
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.646e+01 5.103e+00 7.144 3.28e-12 ***
crim -1.080e-01 3.286e-02 -3.287 0.001087 **
zn 4.642e-02 1.373e-02 3.382 0.000778 ***
indus 2.056e-02 6.150e-02 0.334 0.738288
chas 2.687e+00 8.616e-01 3.118 0.001925 **
nox -1.777e+01 3.820e+00 -4.651 4.25e-06 ***
rm 3.810e+00 4.179e-01 9.116 < 2e-16 ***
age 6.922e-04 1.321e-02 0.052 0.958229
dis -1.476e+00 1.995e-01 -7.398 6.01e-13 ***
rad 3.060e-01 6.635e-02 4.613 5.07e-06 ***
tax -1.233e-02 3.760e-03 -3.280 0.001112 **
ptratio -9.527e-01 1.308e-01 -7.283 1.31e-12 ***
black 9.312e-03 2.686e-03 3.467 0.000573 ***
lstat -5.248e-01 5.072e-02 -10.347 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.745 on 492 degrees of freedom
Multiple R-squared: 0.7406, Adjusted R-squared: 0.7338
F-statistic: 108.1 on 13 and 492 DF, p-value: < 2.2e-16
par(mfrow=c(2, 2))
plot(lm.fit.all)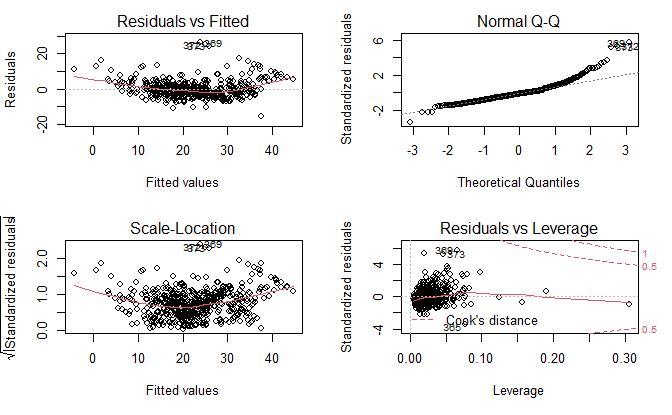
预测
选取 5 条记录
record <- Boston[100:105,]
record["medv"]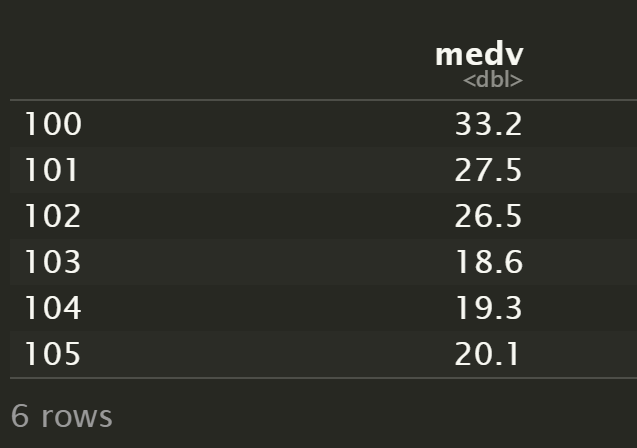
计算预测值
predict(lm.fit.2, record) 100 101 102 103 104 105
28.99328 26.26077 27.76981 25.20196 22.37093 23.60635
predict(lm.fit.all, record) 100 101 102 103 104 105
32.25103 24.58022 25.59413 19.79014 20.31167 21.43483
对比两组结果的残差
record["medv"] - predict(lm.fit.2, record)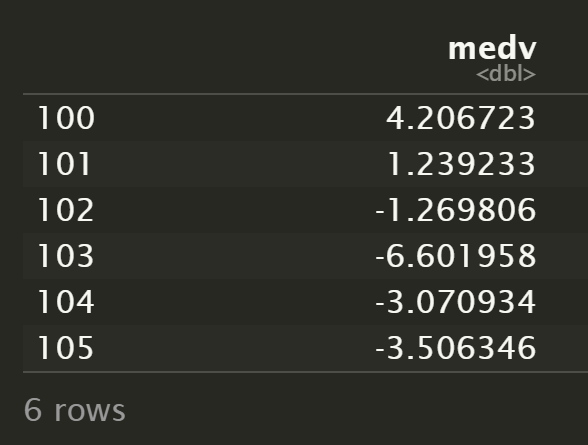
record["medv"] - predict(lm.fit.all, record)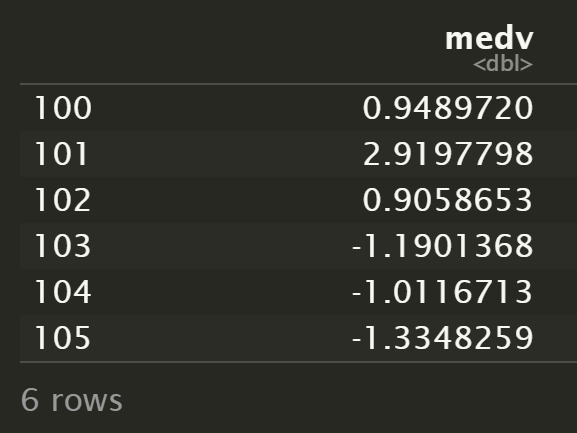
可以看到,全变量拟合模型的预测结果更接近真实值。
预测不确定性
预测有三类不确定性:
- 系数是估计值,可以计算置信区间 (confidence interval) 确定 \hat{y} 与 f(X) 的接近程度。
- 线性模型是对真实模型的一种假设,即存在模型偏差 (model bias)。
- 模型中存在随机误差,即不可约误差 (irreducible error),用预测区间 (prediction interval) 回答 \hat{Y} 与 Y 相差多少的问题。
计算置信区间
predict(
lm.fit.all,
record,
interval="confidence"
) fit lwr upr
1 32.25103 31.02820 33.47385
2 24.58022 23.41753 25.74291
3 25.59413 24.42208 26.76619
4 19.79014 17.75437 21.82590
5 20.31167 19.17509 21.44825
6 21.43483 20.22786 22.64179
计算预测区间
predict(
lm.fit.all,
record,
interval="prediction"
) fit lwr upr
1 32.25103 22.84763 41.65443
2 24.58022 15.18445 33.97599
3 25.59413 16.19721 34.99106
4 19.79014 10.24692 29.33335
5 20.31167 10.91910 29.70424
6 21.43483 12.03348 30.83617
指标
两个最常见的衡量模型拟合优劣的指标是 RSE 和 R^2(方差的解释比例)
可以使用名字访问 summary() 的各个组成部分
R^2
多元线性回归中
R2=Cor(Y,ˆY)2
summary(lm.fit.2)$r.sq[1] 0.5512689
summary(lm.fit.all)$r.sq[1] 0.7406427
全变量拟合结果的 R^2 明显大于两个变量的拟合结果。
RSE
RSE=√1n−p−1RSS
summary(lm.fit.2)$sigma[1] 6.173136
summary(lm.fit.all)$sigma[1] 4.745298
F 统计量
判断响应变量和预测变量之间是否有关系
F=(TSS−RSS)/pRSS/(n−p−1)
其中
TSS=∑(yi−ˉy)2
RSS=∑(yi−^yi)2
summary(lm.fit.all)$fstatistic value numdf dendf
108.0767 13.0000 492.0000
对于包含 q 个变量的特定子集,F 统计量是
F=(RSS0−RSS)/qRSS/(n−p−1)
其中 RSS_0 是除 q 个变量外建立的拟合模型的残差平方和
summary(lm.fit.2)$fstatistic value numdf dendf
308.9693 2.0000 503.0000
当响应变量与预测变量无关时,F 统计量应该接近 1。
根据 F 统计量的 p 值,可以判断预测变量是否与响应变量有关联。
共线性
共线性 (collinearity) 是指两个或更多的预测变量高度相关
多重共线性 (multicollinearity) 可以使用方差膨胀因子 (variance inflation factor, VIF) 评估。
VIF 是拟合全模型时的系数 \beta_j 的方差除以单变量回归中 \beta_j 的方差所得的比例。
VIF 的最小可能值是 1,表示完全不存在共线性。
一个经验法则是,VIF 值超过 5 或 10 就表示有共线性问题。
VIF(^βj)=11−R2Xj|X−j
其中
R2Xj|X−j
是 X_j 对所有预测变量回归的 R^2
计算
car 包的 vif() 函数用于计算方差膨胀因子
library(car)vif(lm.fit.all) crim zn indus chas nox rm age dis rad tax
1.792192 2.298758 3.991596 1.073995 4.393720 1.933744 3.100826 3.955945 7.484496 9.008554
ptratio black lstat
1.799084 1.348521 2.941491
变量选择
variable selection
从拟合结果中可以看到,age 变量有很高的 p 值。 下面用除 age 之外的所有变量进行回归。
lm.fit1 <- lm(medv~.-age, data=Boston)summary(lm.fit1)Call:
lm(formula = medv ~ . - age, data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.6054 -2.7313 -0.5188 1.7601 26.2243
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 36.436927 5.080119 7.172 2.72e-12 ***
crim -0.108006 0.032832 -3.290 0.001075 **
zn 0.046334 0.013613 3.404 0.000719 ***
indus 0.020562 0.061433 0.335 0.737989
chas 2.689026 0.859598 3.128 0.001863 **
nox -17.713540 3.679308 -4.814 1.97e-06 ***
rm 3.814394 0.408480 9.338 < 2e-16 ***
dis -1.478612 0.190611 -7.757 5.03e-14 ***
rad 0.305786 0.066089 4.627 4.75e-06 ***
tax -0.012329 0.003755 -3.283 0.001099 **
ptratio -0.952211 0.130294 -7.308 1.10e-12 ***
black 0.009321 0.002678 3.481 0.000544 ***
lstat -0.523852 0.047625 -10.999 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.74 on 493 degrees of freedom
Multiple R-squared: 0.7406, Adjusted R-squared: 0.7343
F-statistic: 117.3 on 12 and 493 DF, p-value: < 2.2e-16
也可以使用 update() 函数
lm.fit1 <- update(lm.fit, ~.-age)这种方法实际上是后向选择 (backward selection) 方法:
先从包含所有变量的模型开始,删除 p 值最大的变量,即统计学上最不显著的变量。 使用剩余变量继续拟合模型,重复上述步骤直到满足停止条件。
参考
https://github.com/perillaroc/islr-study
ISLR实验系列文章
线性回归
分类
重抽样方法
线性模型选择与正则化
