AMS机器学习课程：预测雷暴旋转的基础机器学习 - 正则化

August 08, 2020 (最后修改: August 22, 2021)

本文翻译自 AMS 机器学习 Python 教程，并有部分修改。
Lagerquist, R., and D.J. Gagne II, 2019: “Basic machine learning for predicting thunderstorm rotation: Python tutorial”. https://github.com/djgagne/ams-ml-python-course/blob/master/module_2/ML_Short_Course_Module_2_Basic.ipynb.

本文接上一篇文章

《AMS机器学习课程：预测雷暴旋转的基础机器学习 - 线性回归》

L1 和 L2 正则化

概括地说，正则化是通过创建更简单的模型来防止过拟合的一种方法。 L1 和 L2 正则鼓励模型具有较小的系数。

当有许多预测因素时，这很有用，因为其中一些预测因素可能与现象之间的因果关系较弱。如果不进行正则化，模型将尝试合并每个预测变量，这可能导致训练数据的特殊性过拟合。正则化鼓励模型只为少量预测变量（真正重要的预测变量）学习大系数。

L1 和 L2 正则化通过向损失函数添加惩罚来鼓励较小的系数。

对于线性回归，损耗函数如下：

\begin{equation*} \epsilon = \frac{1}{N} \sum\limits_{i = 1}^{N} (\hat{y}i - y_i)^2 + \lambda_1 \sum\limits{j = 1}^{M} \lvert \beta_j \rvert + \lambda_2 \sum\limits_{j = 1}^{M} \beta_j^2 = \textrm{MSE} + \lambda_1 \sum\limits_{j = 1}^{M} \lvert \beta_j \rvert + \lambda_2 \sum\limits_{j = 1}^{M} \beta_j^2 \end{equation*}

第一项就是均方误差（Mean Squared Error，MSE）。

第二项是 L1 惩罚项。 lambda_{1} 是 L1 惩罚项的强度，sum{beta_{j} 是系数绝对值之和。

第三项是 L2 惩罚项。 lambda_{2} 是 L2 惩罚项的强度，sum{beta^{2}_{j}} 是系数的平方和。

这两种惩罚都鼓励较小的系数，但 L1 惩罚也鼓励更小的非零系数。这是因为 L1 惩罚不计算系数的平方值。对于小系数值，L2 惩罚将变得微不足道，除非 L2 非常大。例如，将系数 10^{-3} 计算为 10^{-6}，此惩罚通常可以忽略不计。

因此，L1 惩罚称为“lasso penalty”（它抛出套索，只将预测器放在套索内）。 L2 惩罚称为“ridge penalty”。

带 L2 惩罚项的线性回归

示例

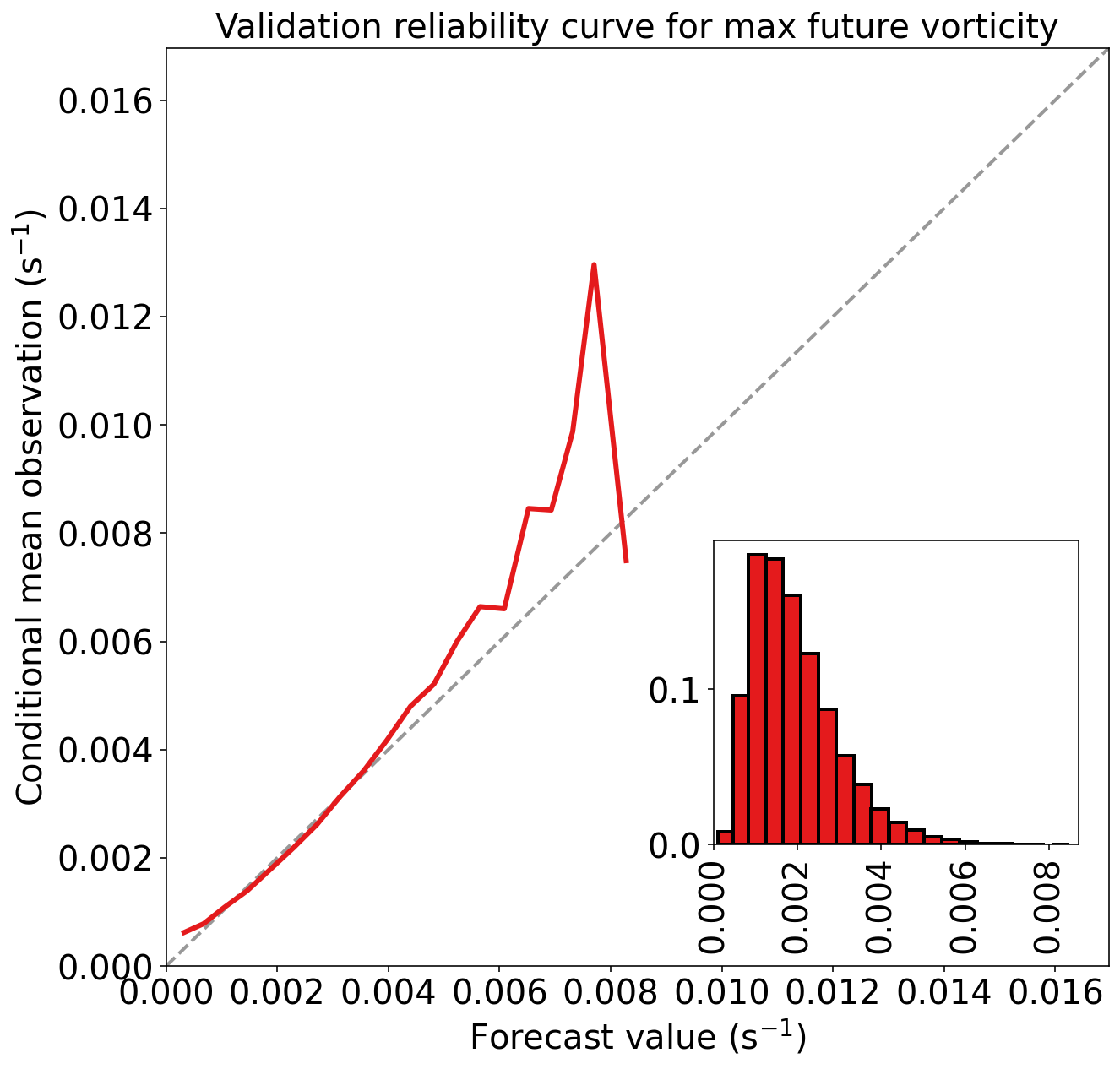
下一个单元格仅训练只有 L2 惩罚的线性回归模型。正则强度（ lambda2 ）为 10^5 。

请注意，训练和验证性能都变得更差。这意味着尝试的 labmda2 值过高。

构造模型

linear_ridge_model_object = setup_linear_regression(
    lambda1=0.,
    lambda2=1e5,
)
linear_ridge_model_object

Ridge(alpha=100000.0, random_state=6695)

训练模型

train_linear_regression(
    model=linear_ridge_model_object,
    training_predictor_table=training_predictor_table,
    training_target_table=training_target_table,
)

预测结果

training_predictions = linear_ridge_model_object.predict(
    training_predictor_table.values
)
mean_training_target_value = np.mean(
    training_target_table[TARGET_NAME].values
)

训练集性能

_ = evaluate_regression(
    target_values=training_target_table[TARGET_NAME].values,
    predicted_target_values=training_predictions,
    mean_training_target_value=mean_training_target_value,
    dataset_name="training",
)

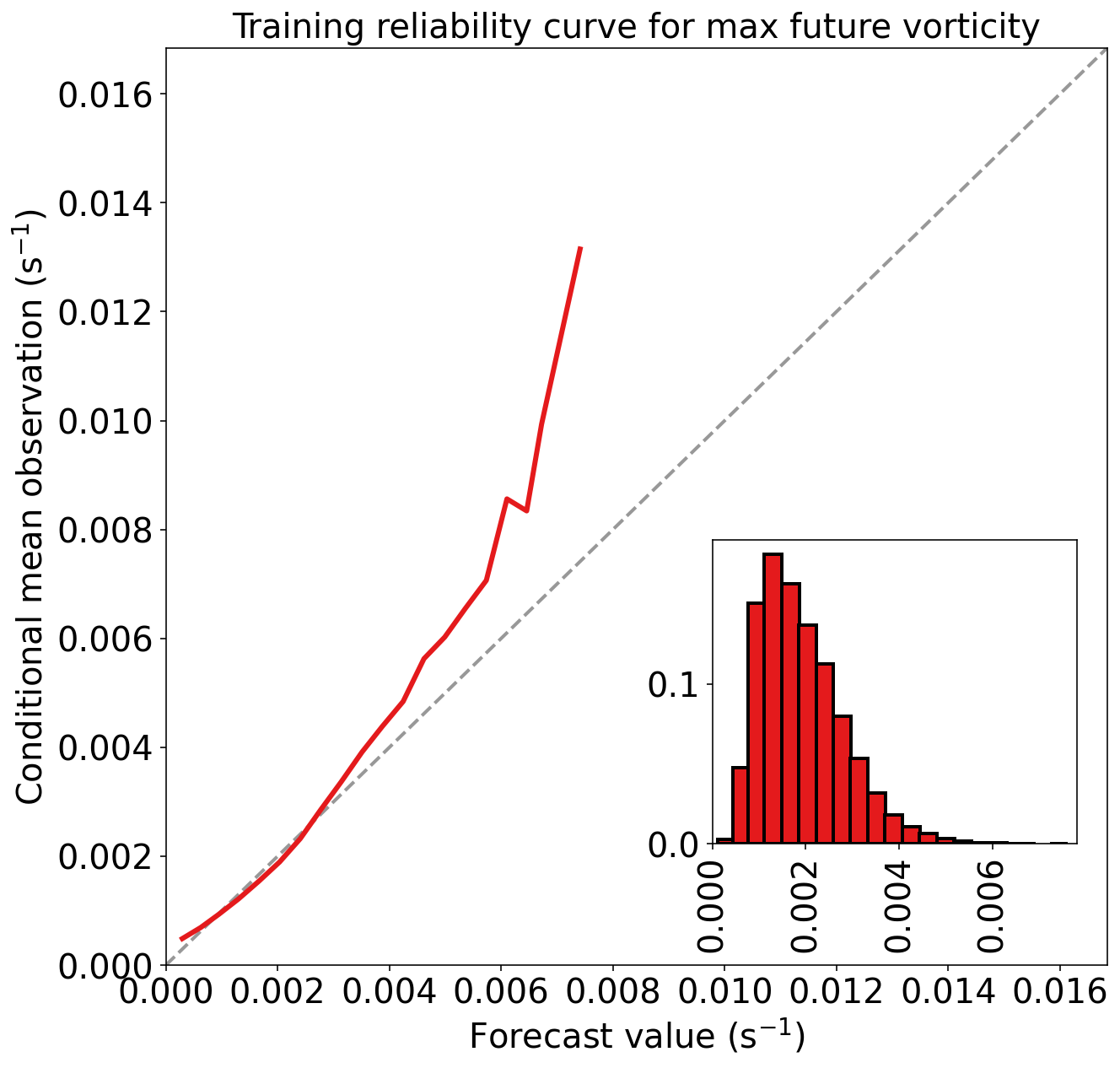
Training MAE (mean absolute error) = 8.120e-04 s^-1
Training MSE (mean squared error) = 1.255e-06 s^-2
Training bias (mean signed error) = 3.256e-19 s^-1
Training MAE skill score (improvement over climatology) = 0.279
Training MSE skill score (improvement over climatology) = 0.460

验证集性能

validation_predictions = linear_ridge_model_object.predict(
    validation_predictor_table.values
)
_ = evaluate_regression(
    target_values=validation_target_table[TARGET_NAME].values,
    predicted_target_values=validation_predictions,
    mean_training_target_value=mean_training_target_value,
    dataset_name="validation"
)

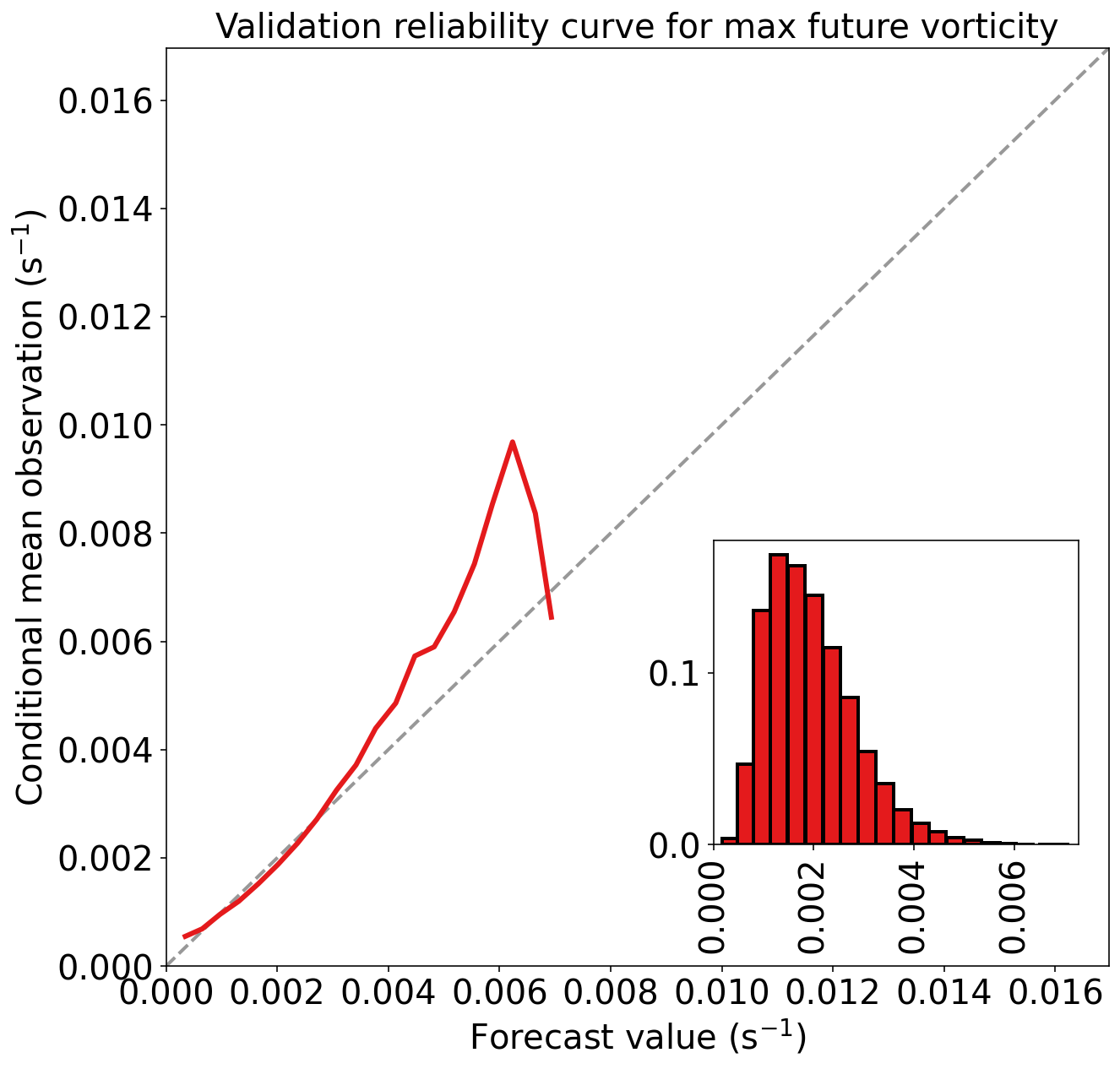
Validation MAE (mean absolute error) = 7.910e-04 s^-1
Validation MSE (mean squared error) = 1.193e-06 s^-2
Validation bias (mean signed error) = 7.027e-06 s^-1
Validation MAE skill score (improvement over climatology) = 0.279
Validation MSE skill score (improvement over climatology) = 0.477

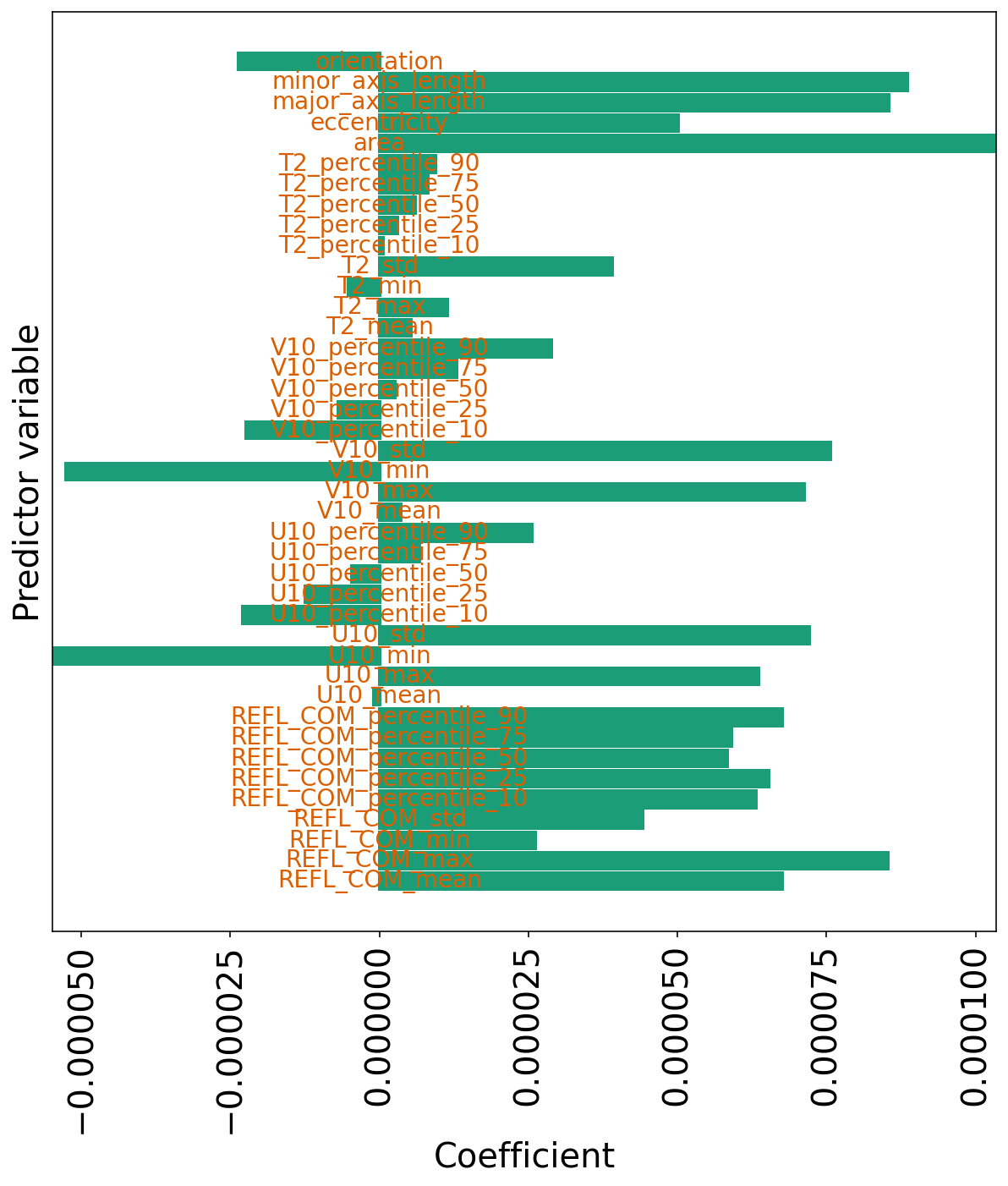
系数

下一个单元格仅绘制只有 L2 惩罚项的线性回归系数。

请注意，系数通常比原始模型（10^{-5} 到 10^{-4}，而不是 10^{-4} 到 10^{-3}）中的数量级小。

但是，所有系数都是非零的，因为正如所讨论的，L2 惩罚不鼓励系数完全为零。

plot_model_coefficients(
    model=linear_ridge_model_object,
    predictor_names=list(training_predictor_table),
)

带 L1 惩罚项的线性回归

示例

下一个单元格仅训练只有 L1 惩罚项的线性回归模型。正则强度（ lambda_{1} ）为 10^{-5}。

训练和验证性能都比原始模型差一些，这意味着 lambda_{1} 值太高。

但是，性能的降低程度不像 L2 正则化那样大。

构建模型

linear_lasso_model_object = setup_linear_regression(
    lambda1=1e-5,
    lambda2=0.
)
linear_lasso_model_object

Lasso(alpha=1e-05, random_state=6695)

训练模型

_ = train_linear_regression(
    model=linear_lasso_model_object,
    training_predictor_table=training_predictor_table,
    training_target_table=training_target_table,
)

计算预测结果

training_predictions = linear_lasso_model_object.predict(
    training_predictor_table.values
)
mean_training_target_value = np.mean(
    training_target_table[TARGET_NAME].values
)

评估训练集性能

_ = evaluate_regression(
    target_values=training_target_table[TARGET_NAME].values,
    predicted_target_values=training_predictions,
    mean_training_target_value=mean_training_target_value,
    dataset_name="traning",
)

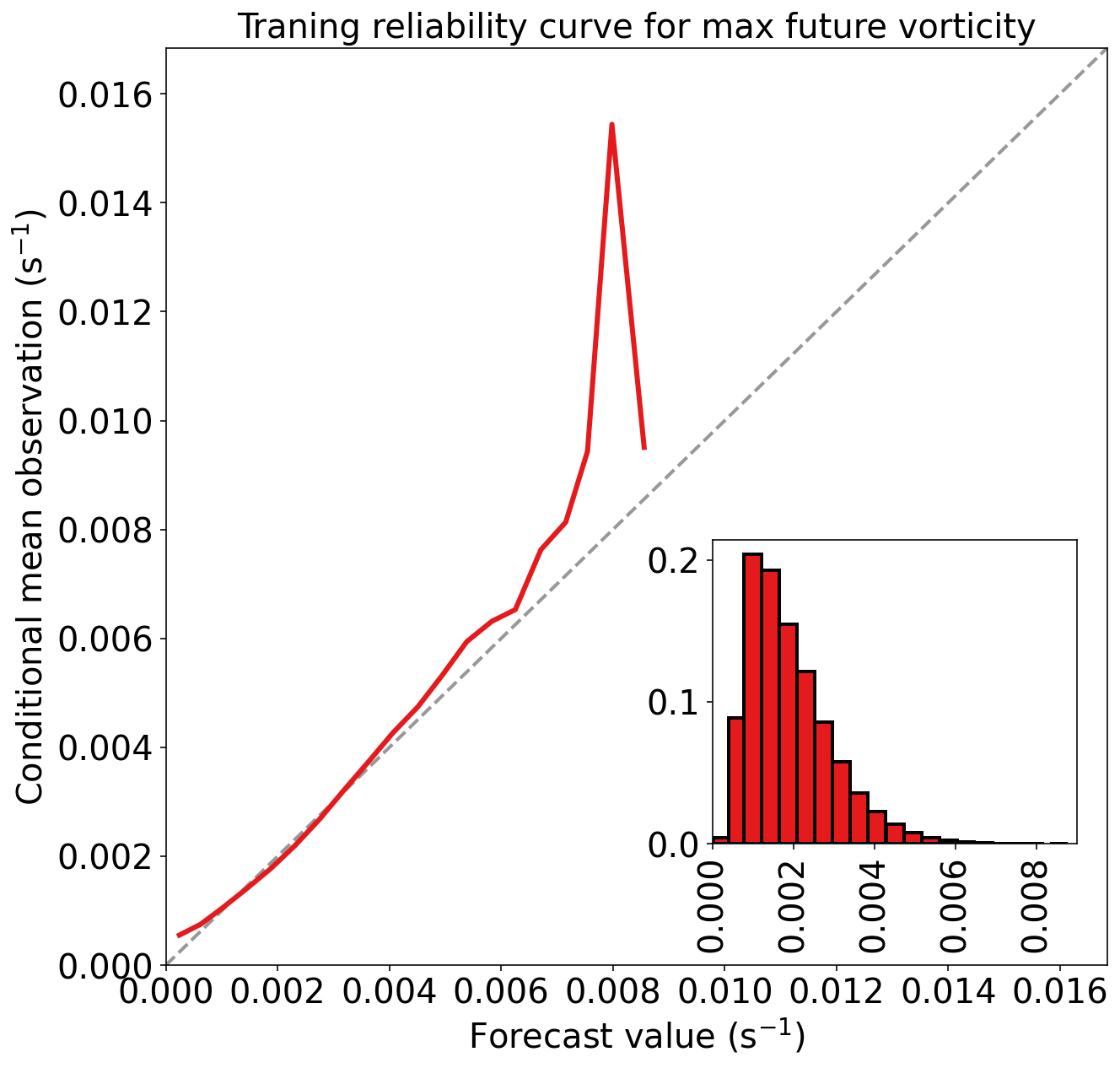
Traning MAE (mean absolute error) = 7.893e-04 s^-1
Traning MSE (mean squared error) = 1.168e-06 s^-2
Traning bias (mean signed error) = 1.635e-19 s^-1
Traning MAE skill score (improvement over climatology) = 0.299
Traning MSE skill score (improvement over climatology) = 0.497

评估验证集性能

validation_predictions = linear_lasso_model_object.predict(
    validation_predictor_table.values
)
_ = evaluate_regression(
    target_values=validation_target_table[TARGET_NAME].values,
    predicted_target_values=validation_predictions,
    mean_training_target_value=mean_training_target_value,
    dataset_name="validation",
)

Validation MAE (mean absolute error) = 7.669e-04 s^-1
Validation MSE (mean squared error) = 1.103e-06 s^-2
Validation bias (mean signed error) = 1.086e-06 s^-1
Validation MAE skill score (improvement over climatology) = 0.301
Validation MSE skill score (improvement over climatology) = 0.516

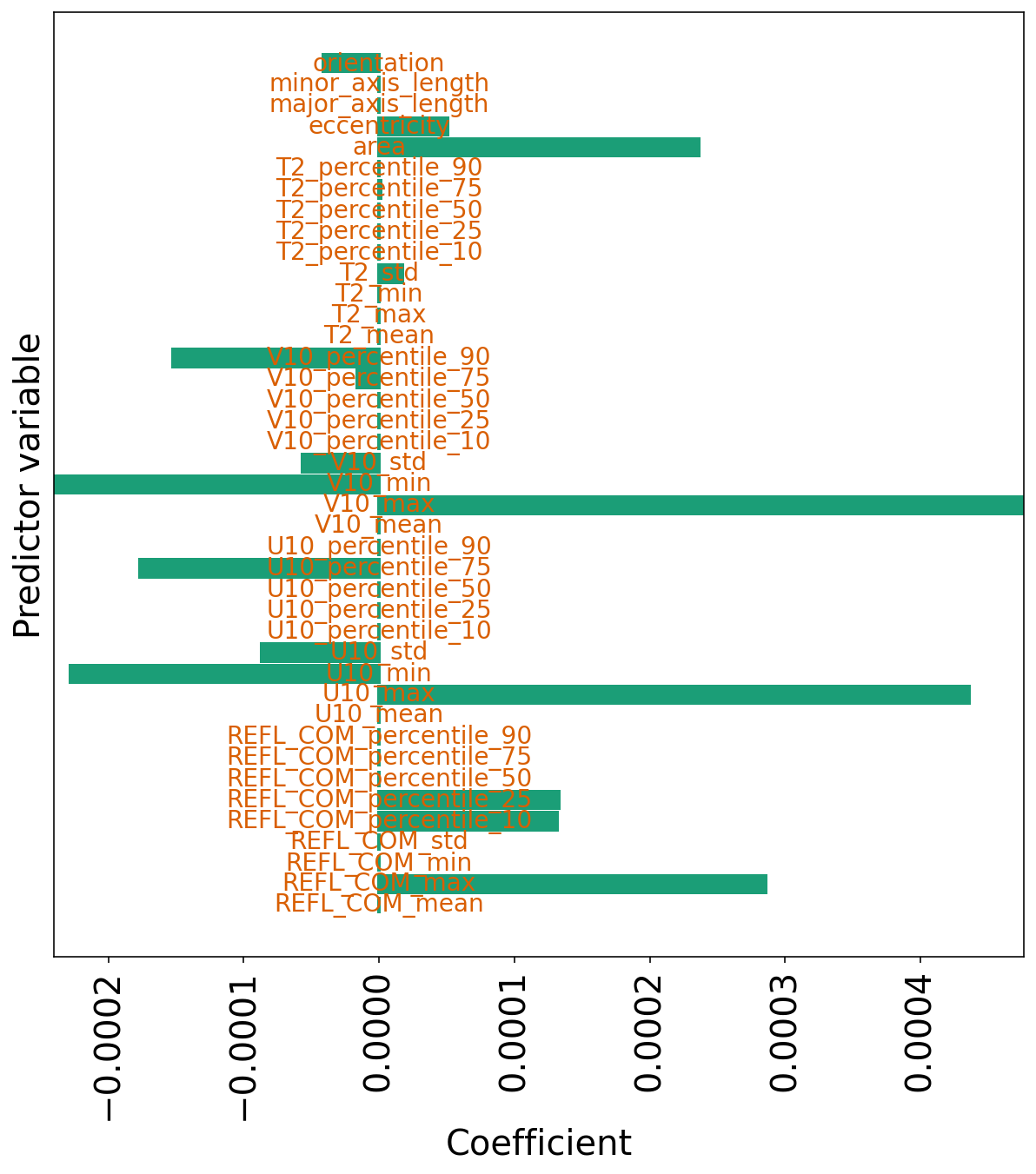
系数

下一个单元格绘制仅带有 L1 惩罚项的线性回归系数。

非零系数通常与原始模型处于相同的数量级（~10^{-4}）。

但是，许多系数（41 个中的 25 个）已被“置零”。这意味着该模型仅使用 41 个预测变量中的 16 个。

（注意：如果您再次运行模型，此结果可能会略有不同，因为作者不确定是否所有随机性都已得到控制。）

plot_model_coefficients(
    model=linear_lasso_model_object,
    predictor_names=list(training_predictor_table)
)

译者注：变量中包含 T2 等要素的百分位数、均值、方差、最值等等，这些数值不是完全独立分布的，具有一定的相关性。从这一角度也许可以解释为什么一半的预测变量都没被使用。

带 L1 和 L2 惩罚项的线性回归

示例

下一个单元格训练带两个惩罚项的线性回归模型。仅有 L1 惩罚项的模型被称为 lasso penlty，仅有 L2 惩罚项的模型被称为 ridge penalty，而这类模型被称为 elastic net。

在文献中，您可能会看到人们谈论“lasso regression”，“ridge regression”和“elastic-net regression”。这些不是实体。lasso，ridge 和 elastic-net 惩罚可以应用于任何类型的模型。当人们说“lasso regression”，“ridge regression”和“elastic-net regression”时，它们通常表示具有给定惩罚的线性回归。然而，这不总是正确的，所以请小心注意。

在该弹性网络中，训练集和验证集的性能“更差”，因为惩罚项的值太高（lambda_1 = 10^-5 且 lambda_2 = 5）。

构建线性回归模型

linear_en_model_object = setup_linear_regression(
    lambda1=1e-5,
    lambda2=5.
)
linear_en_model_object

ElasticNet(alpha=5.00001, l1_ratio=1.9999960000080004e-06, random_state=6695)

训练模型

_ = train_linear_regression(
    model=linear_en_model_object,
    training_predictor_table=training_predictor_table,
    training_target_table=training_target_table,
)

预测结果

training_predictions = linear_en_model_object.predict(
    training_predictor_table.values
)

评估训练集性能

mean_training_target_value = np.mean(
    training_target_table[TARGET_NAME].values
)

_ = evaluate_regression(
    target_values=training_target_table[TARGET_NAME].values,
    predicted_target_values=training_predictions,
    mean_training_target_value=mean_training_target_value,
    dataset_name="training",
)

Training MAE (mean absolute error) = 8.554e-04 s^-1
Training MSE (mean squared error) = 1.396e-06 s^-2
Training bias (mean signed error) = 3.518e-19 s^-1
Training MAE skill score (improvement over climatology) = 0.241
Training MSE skill score (improvement over climatology) = 0.399

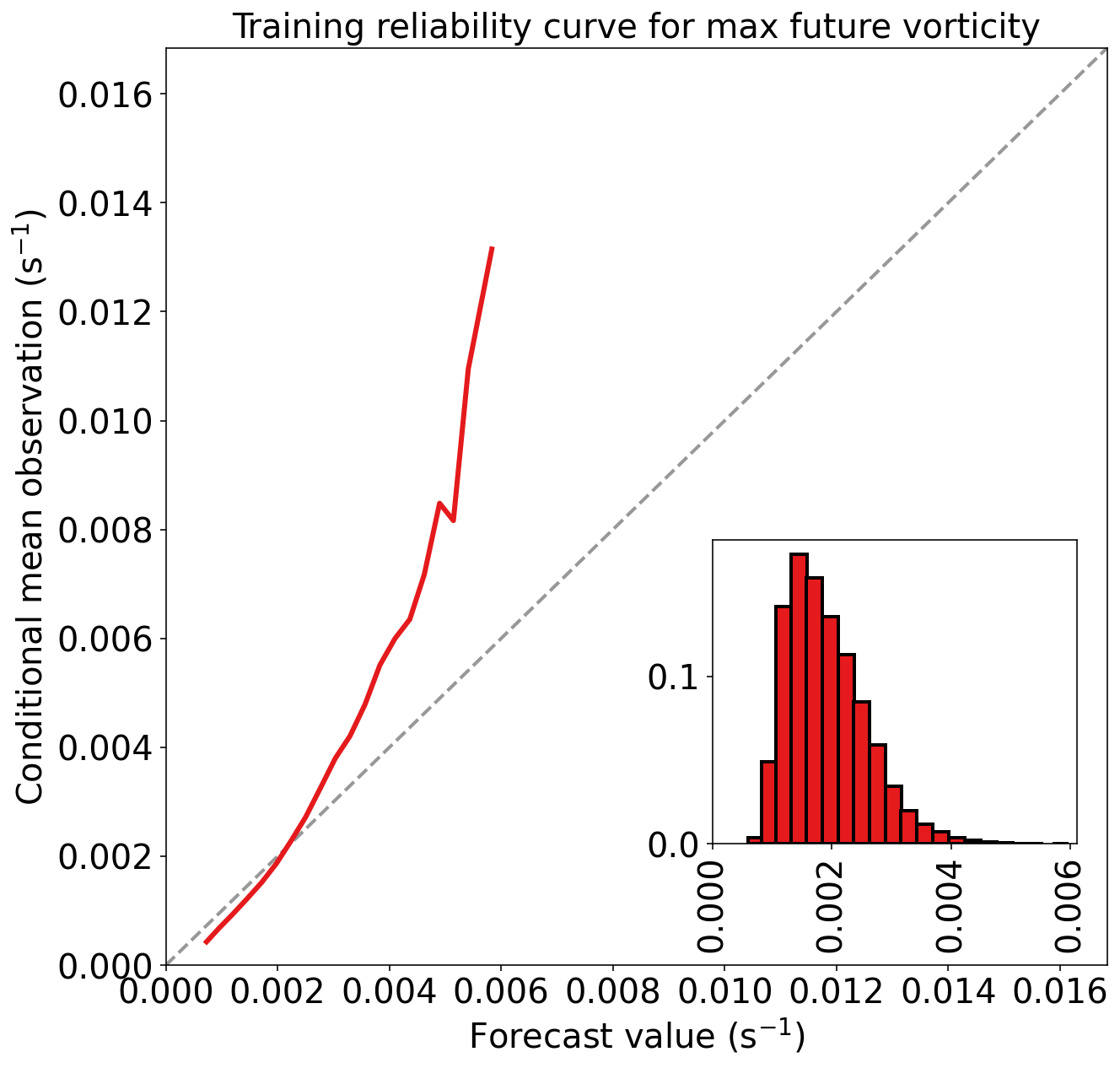
验证集性能

validation_predictions = linear_en_model_object.predict(
    validation_predictor_table.values
)

_ = evaluate_regression(
    target_values=validation_target_table[TARGET_NAME].values,
    predicted_target_values=validation_predictions,
    mean_training_target_value=mean_training_target_value,
    dataset_name='validation'
)

Validation MAE (mean absolute error) = 8.370e-04 s^-1
Validation MSE (mean squared error) = 1.344e-06 s^-2
Validation bias (mean signed error) = 4.480e-06 s^-1
Validation MAE skill score (improvement over climatology) = 0.237
Validation MSE skill score (improvement over climatology) = 0.410

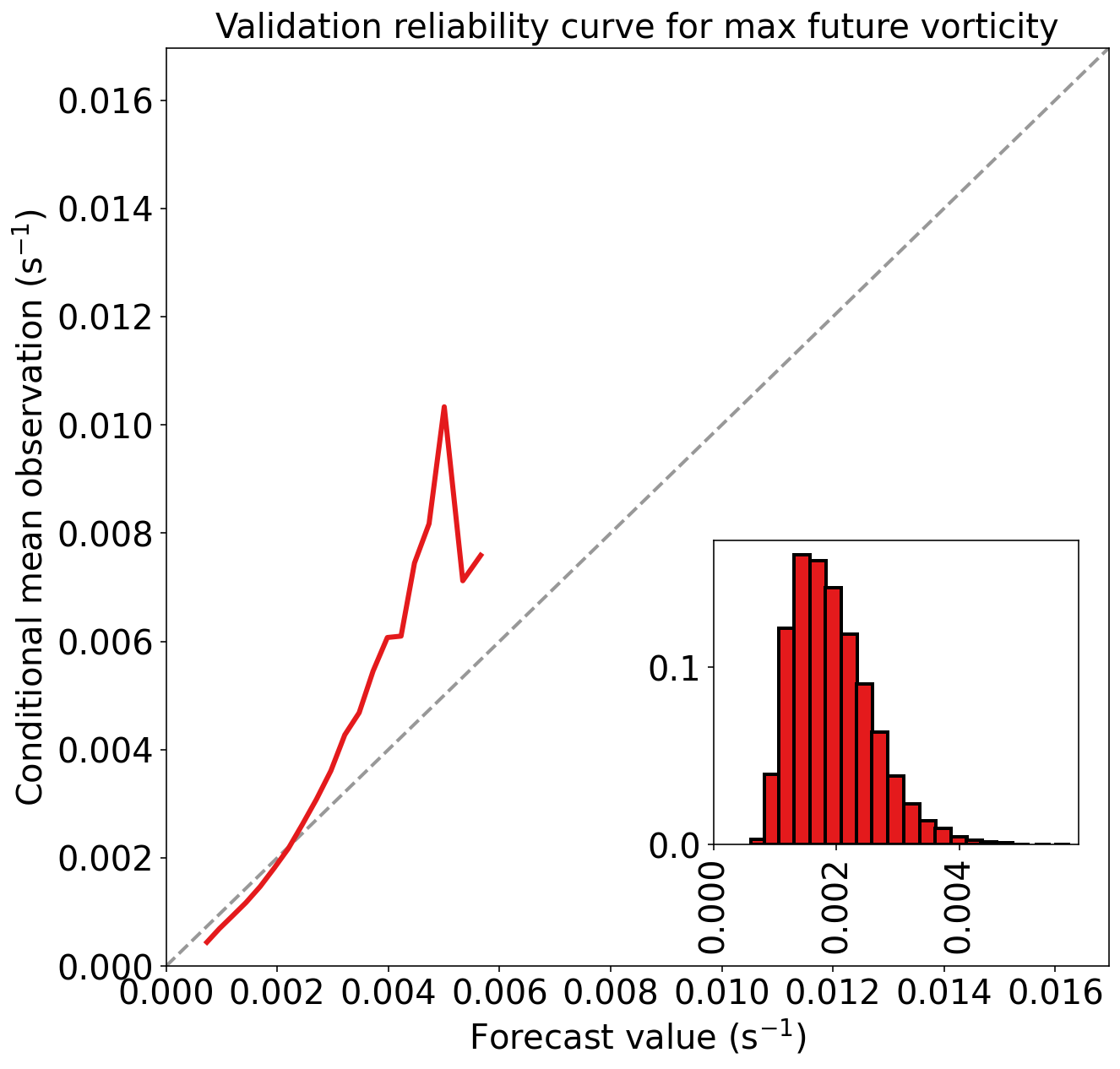
系数

下一个单元格绘制了具有两个惩罚项的线性回归系数。

通常，系数比原始模型小一个数量级。而且，零系数并不多。

这意味着，在选择 lambda_1 和 lambda_2 的情况下，L2 正则化将“淹没” L1 正则化。

plot_model_coefficients(
    model=linear_en_model_object,
    predictor_names=list(training_predictor_table)
)
pyplot.show()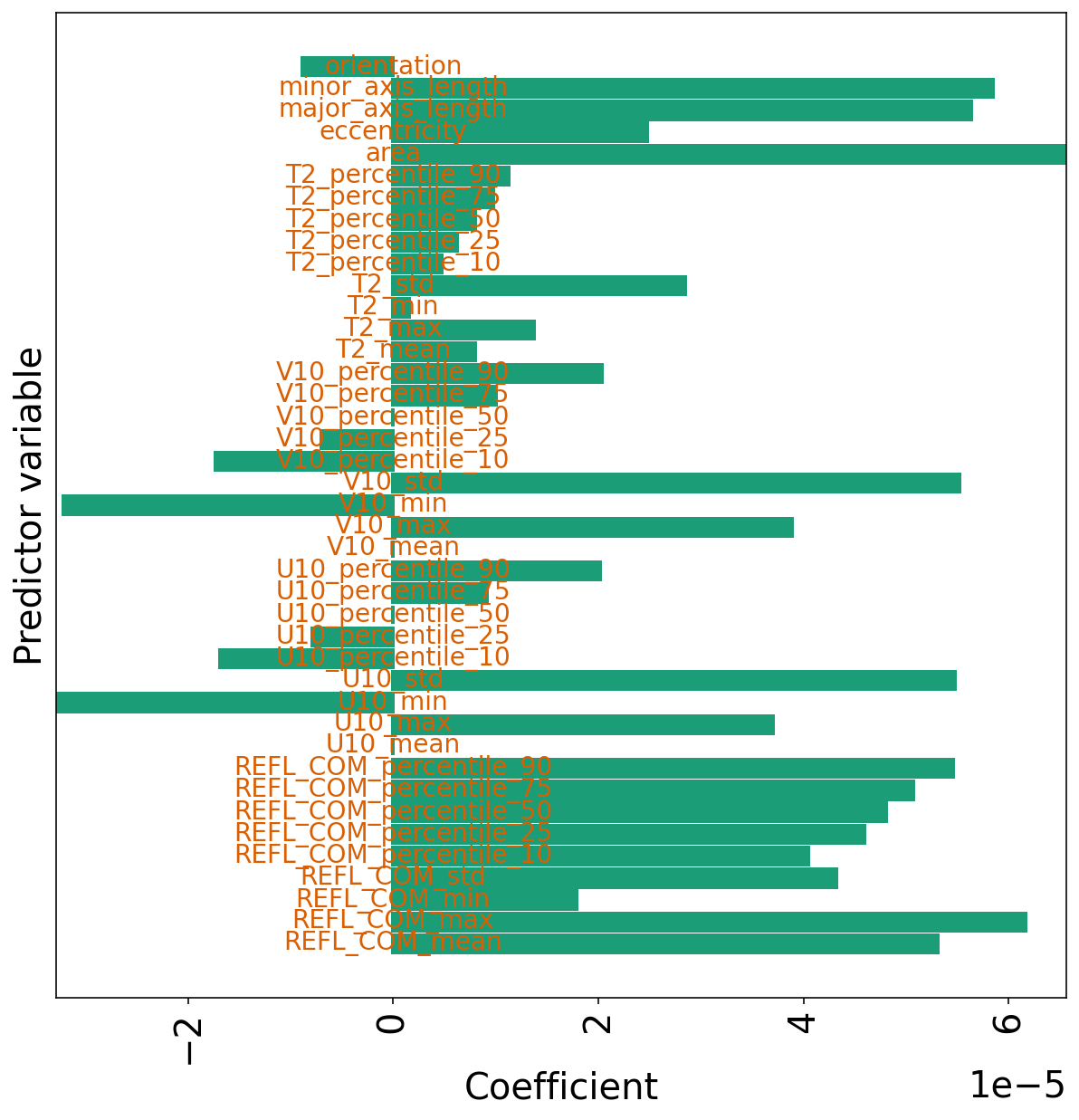

练习

用您自己的 lambda_1 和 lambda_2 值训练线性回归模型。研究在训练和验证数据集上的性能，并绘制系数。

参考

https://github.com/djgagne/ams-ml-python-course

AMS 机器学习课程

《AMS机器学习课程：数据分析与预处理》

《AMS机器学习课程：预测雷暴旋转的基础机器学习 - 数据》

《AMS机器学习课程：预测雷暴旋转的基础机器学习 - 线性回归》