AMS机器学习课程：预测雷暴旋转的基础机器学习 - 线性回归

August 07, 2020 (最后修改: August 22, 2021)

本文翻译自 AMS 机器学习 Python 教程，并有部分修改。
Lagerquist, R., and D.J. Gagne II, 2019: “Basic machine learning for predicting thunderstorm rotation: Python tutorial”. https://github.com/djgagne/ams-ml-python-course/blob/master/module_2/ML_Short_Course_Module_2_Basic.ipynb.

本文接上一篇文章

《AMS机器学习课程：预测雷暴旋转的基础机器学习 - 数据》

线性回归

线性回归将以下方程与训练数据拟合

$$ \hat{y} = \beta_0 + \sum\limits_{j = 1}^{M} \beta_j x_j $$

x_j 是第 j 个预测变量
beta_j 是第 j 个预测变量的系数，在训练过程中会被调整
M 是预测变量的数目
beta_0 是偏置系数或截距，在训练过程中会被调整
hat{y} 是对目标变量的预测，在本例中，是未来风暴中最大的涡度，单位是每秒

权重（beta_0 和 beta_j）经过训练以使均方误差（Mean Squared Error，MSE）最小。这也是为什么线性回归会被称为“最小二乘线性回归”。

\begin{equation*} \textrm{MSE} = \frac{1}{N} \sum\limits_{i = 1}^{N} (\hat{y}_i - y_i)^2 \end{equation*}

y_i 是第 i 个样本的实际目标值。在本例中，一个示例是一次一个风暴单元，或者一个“风暴对象”
hat{y_i} 是第 i 个样本的预测目标值
N 是训练样本的数量

将上面两个等值合并可以得到下面的等式，其中 x_{ij} 是第 j 个预测变量的第 i 个样本

\begin{equation*} \textrm{MSE} = \frac{1}{N} \sum\limits_{i = 1}^{N} (\beta_0 + \sum\limits_{j = 1}^{M} \beta_j x_{ij} - y_i)^2 \end{equation*}

模型系数与 MSE 的导数如下：

\begin{equation*} \frac{\partial}{\partial \beta_0}(\textrm{MSE}) = \frac{2}{N} \sum\limits_{i = 1}^{N} (\hat{y}_i - y_i) \end{equation*}

\begin{equation*} \frac{\partial}{\partial \beta_j}(\textrm{MSE}) = \frac{2}{N} \sum\limits_{i = 1}^{N} x_{ij} (\hat{y}_i - y_i) \end{equation*}

在训练期间，权重（beta_0 和 beta_j）经过多次迭代调整。

每次迭代后，将应用“梯度下降规则”（如下所示），其中 alpha 在 (0, 1] 之间，表示学习率。

\begin{equation*} \beta_0 \leftarrow \beta_0 - \alpha \frac{\partial}{\partial \beta_0}(\textrm{MSE}) \end{equation*}

\begin{equation*} \beta_j \leftarrow \beta_j - \alpha \frac{\partial}{\partial \beta_j}(\textrm{MSE}) \end{equation*}

线性回归：示例

下一个单元格执行以下操作：

训练线性回归模型（具有默认的超参数），以预测每次暴风雨中未来的最大旋转量
在训练和验证数据集上评估模型

对于训练和验证数据，本教程汇报以下统计指标：

平均绝对误差（Mean Abosolute Error，MAE）

\begin{equation*} \frac{1}{N} \sum\limits_{i = 1}^{N} \lvert \hat{y}_i - y_i \rvert \end{equation*}

均方误差（Mean Squared Error，MSE）

\begin{equation*} \frac{1}{N} \sum\limits_{i = 1}^{N} (\hat{y}_i - y_i)^2 \end{equation*}

偏差（Mean signed error，bias）

\begin{equation*} \frac{1}{N} \sum\limits_{i = 1}^{N} (\hat{y}_i - y_i) \end{equation*}

MAE 技巧评分。定义如下，其中 MAE 是模型的 MAE，MAE_{climo} 是通过始终预测“气候”（训练数据中的平均值）而获得的 MAE。

\begin{equation*} \textrm{MAE skill score} = \frac{\textrm{MAE}{\textrm{climo}} - \textrm{MAE}}{\textrm{MAE}{\textrm{climo}}} \end{equation*}

MSE 技巧评分。定义如下

\begin{equation*} \textrm{MSE skill score} = \frac{\textrm{MSE}{\textrm{climo}} - \textrm{MSE}}{\textrm{MSE}{\textrm{climo}}} \end{equation*}

最后，此单元格绘制了一条可靠性曲线（reliability curve），该曲线显示了每个预测值的条件平均观察值。这使您可以确定条件偏差（某些预测值发生的偏差）。

创建线性回归模型对象

其中 labmda1 和 lambda2 表示 L1 和 L2 正则化权重，根据不同的设置返回四种模型：

LinearRegression：线性回归
Ridge：岭回归
Lasso：Lasso 回归
ElasticNet：弹性网络回归

# 忽略较小的系数
LAMBDA_TOLERANCE = 1e-10

# 示例使用固定的随机数种子，尽量保证每次运行结果一致
RANDOM_SEED = 6695

# 生成用于 Elastic Net 回归模型的系数
def _lambdas_to_sklearn_inputs(lambda1, lambda2):
    return lambda1 + lambda2, lambda1 / (lambda1 + lambda2)

def setup_linear_regression(lambda1=0., lambda2=0.):
    assert lambda1 >= 0
    assert lambda2 >= 0
    
    # 不使用正则化返回线性回归对象
    if lambda1 < LAMBDA_TOLERANCE and lambda2 < LAMBDA_TOLERANCE:
        return linear_model.LinearRegression(
            fit_intercept=True, normalize=False)
    
    # 仅使用 L2 正则化，返回 Ridge 回归对象
    if lambda1 < LAMBDA_TOLERANCE:
        return linear_model.Ridge(
            alpha=lambda2, fit_intercept=True, normalize=False,
            random_state=RANDOM_SEED)
    
    # 仅使用 L1 正则化，返回 Lasso 回归对象
    if lambda2 < LAMBDA_TOLERANCE:
        return linear_model.Lasso(
            alpha=lambda1, fit_intercept=True, normalize=False,
            random_state=RANDOM_SEED)
    
    # 同时使用 L1 和 L2 正则化，返回 ElasticNet 回归对象
    alpha, l1_ratio = _lambdas_to_sklearn_inputs(
        lambda1=lambda1, lambda2=lambda2)
    
    return linear_model.ElasticNet(
        alpha=alpha, 
        l1_ratio=l1_ratio, 
        fit_intercept=True, 
        normalize=False,
        random_state=RANDOM_SEED
    )

生成一个线性回归模型对象

linreg_model_object = setup_linear_regression(
    lambda1=0.,
    lambda2=0.,
)
linreg_model_object

LinearRegression()

训练模型

train_linear_regression 函数用于训练线性模型

注：scikit-learn 的模型对象都有 fit 方法用于训练。

def train_linear_regression(
    model, 
    training_predictor_table: pd.DataFrame,
    training_target_table: pd.DataFrame
):
    model.fit(
        X=training_predictor_table.values,
        y=training_target_table[TARGET_NAME].values
    )

    return model

使用训练集训练模型

_ = train_linear_regression(
    model=linreg_model_object,
    training_predictor_table=training_predictor_table,
    training_target_table=training_target_table,
)

预测结果

计算预测目标

注：scikit-learn 的模型对象都有 predict 方法用于计算预测结果

training_predictions = linreg_model_object.predict(
    training_predictor_table.values
)

计算目标变量的均值

mean_training_target_value = np.mean(
    training_target_table[TARGET_NAME].values
)
mean_training_target_value

0.001910818440106315

评估模型

使用到的函数

evluate_regression 函数用于评估回归模型，输出统计指标并绘制图形。

MAE_KEY = 'mean_absolute_error'
MSE_KEY = 'mean_squared_error'
MEAN_BIAS_KEY = 'mean_bias'
MAE_SKILL_SCORE_KEY = 'mae_skill_score'
MSE_SKILL_SCORE_KEY = 'mse_skill_score'


def evaluate_regression(
    target_values:np.ndarray, 
    predicted_target_values:np.ndarray, 
    mean_training_target_value:float,
    verbose=True, 
    create_plots=True, 
    dataset_name=None
):
    signed_errors = predicted_target_values - target_values
    
    # 平均偏差
    mean_bias = np.mean(signed_errors)
    
    # 平均绝对误差
    mean_absolute_error = np.mean(np.absolute(signed_errors))
    
    # 均方误差
    mean_squared_error = np.mean(signed_errors ** 2)

    climo_signed_errors = mean_training_target_value - target_values
    climo_mae = np.mean(np.absolute(climo_signed_errors))
    climo_mse = np.mean(climo_signed_errors ** 2)
    
    # MAE 技巧评分，[-1, 1] 之间，相对于气候场的改进
    mae_skill_score = (climo_mae - mean_absolute_error) / climo_mae
    
    # MSE 技巧评分，[-1, 1] 之间，相对于气候场的改进
    mse_skill_score = (climo_mse - mean_squared_error) / climo_mse

    evaluation_dict = {
        MAE_KEY: mean_absolute_error,
        MSE_KEY: mean_squared_error,
        MEAN_BIAS_KEY: mean_bias,
        MAE_SKILL_SCORE_KEY: mae_skill_score,
        MSE_SKILL_SCORE_KEY: mse_skill_score
    }

    if verbose or create_plots:
        dataset_name = dataset_name[0].upper() + dataset_name[1:]
    
    # 输出统计结果
    if verbose:
        print(
            f'{dataset_name} MAE (mean absolute error) '
            f'= {evaluation_dict[MAE_KEY]:.3e} s^-1')
        print(
            f'{dataset_name} MSE (mean squared error) '
            f'= {evaluation_dict[MSE_KEY]:.3e} s^-2'
        )
        print(
            f'{dataset_name} bias (mean signed error) '
            f'= {evaluation_dict[MEAN_BIAS_KEY]:.3e} s^-1'
        )

        print(
            f'{dataset_name} MAE skill score (improvement over climatology) '
            f'= {evaluation_dict[MAE_SKILL_SCORE_KEY]:.3f}'
        )

        print(
            f'{dataset_name} MSE skill score (improvement over climatology) '
            f'= {evaluation_dict[MSE_SKILL_SCORE_KEY]:.3f}'
        )

    if not create_plots:
        return evaluation_dict
    
    # 绘制统计图形
    figure_object, axes_object = pyplot.subplots(
        1, 1, 
        figsize=(10, 10)
    )

    plot_regression_relia_curve(
        observed_values=target_values, 
        forecast_values=predicted_target_values,
        num_bins=20, 
        figure_object=figure_object, 
        axes_object=axes_object
    )

    axes_object.set_xlabel(r'Forecast value (s$^{-1}$)')
    axes_object.set_ylabel(r'Conditional mean observation (s$^{-1}$)')

    title_string = f'{dataset_name} reliability curve for max future vorticity'
    axes_object.set_title(title_string)
    pyplot.show()

    return evaluation_dict

画图相关函数

plot_regression_relia_curve 函数用于绘制线性回归的可靠性曲线

DEFAULT_NUM_BINS = 20

def plot_regression_relia_curve(
    observed_values, 
    forecast_values, 
    num_bins: int=DEFAULT_NUM_BINS,
    figure_object=None, 
    axes_object=None
):
    # 获取可靠性曲线需要的数据：
    #     预报数据在每个桶内的平均值
    #     观测数据在每个桶内的平均值
    #     每个桶内样本的个数
    mean_forecast_by_bin, mean_observation_by_bin, num_examples_by_bin = (
        _get_points_in_regression_relia_curve(
            observed_values=observed_values, 
            forecast_values=forecast_values,
            num_bins=num_bins)
    )

    if figure_object is None or axes_object is None:
        figure_object, axes_object = pyplot.subplots(
            1, 1, 
            figsize=(10, 10)
        )
    
    # 绘制预报数据每个桶均值的直方图
    _plot_forecast_hist_for_regression(
        figure_object=figure_object, 
        mean_forecast_by_bin=mean_forecast_by_bin,
        num_examples_by_bin=num_examples_by_bin)

    max_forecast_or_observed = max([
        np.max(forecast_values), 
        np.max(observed_values)
    ])
    
    # 绘制完美情况：y = x 的直线
    perfect_x_coords = np.array(
        [0., max_forecast_or_observed]
    )
    perfect_y_coords = perfect_x_coords + 0.
    axes_object.plot(
        perfect_x_coords, 
        perfect_y_coords, 
        color=np.full(3, 152. / 255),
        linestyle='dashed', 
        linewidth=2,
    )

    # 绘制真实情况
    # 获取非 NaN 值的索引，仅绘制有效值
    real_indices = np.where(
        np.invert(
            np.logical_or(
                np.isnan(mean_forecast_by_bin), 
                np.isnan(mean_observation_by_bin),
            )
        )
    )[0]

    axes_object.plot(
        mean_forecast_by_bin[real_indices],
        mean_observation_by_bin[real_indices],
        color=np.array([228, 26, 28], dtype=float) / 255,
        linestyle='solid', 
        linewidth=3
    )

    axes_object.set_xlabel('Forecast value')
    axes_object.set_ylabel('Conditional mean observation')
    axes_object.set_xlim(0., max_forecast_or_observed)
    axes_object.set_ylim(0., max_forecast_or_observed)

注：

np.logical_or：逻辑或
np.invert：取非

_get_points_in_regression_relia_curve 函数创建可靠性曲线需要的数据点

def _get_points_in_regression_relia_curve(
    observed_values: np.ndarray, 
    forecast_values: np.ndarray,
    num_bins: int,
):
    # 预测数据的桶序号
    inputs_to_bins = _get_histogram(
        input_values=forecast_values, 
        num_bins=num_bins,
        min_value=np.min(forecast_values),
        max_value=np.max(forecast_values)
    )
    
    # 预报数据在每个桶的均值
    mean_forecast_by_bin = np.full(num_bins, np.nan)
    
    # 每个桶对应的观测值的均值
    mean_observation_by_bin = np.full(num_bins, np.nan)
    
    # 每个桶的样本个数
    num_examples_by_bin = np.full(num_bins, -1, dtype=int)

    for k in range(num_bins):
        # 属于桶 k 的预报数据的索引
        these_example_indices = np.where(inputs_to_bins == k)[0]
        
        num_examples_by_bin[k] = len(these_example_indices)

        mean_forecast_by_bin[k] = np.mean(
            forecast_values[these_example_indices]
        )

        mean_observation_by_bin[k] = np.mean(
            observed_values[these_example_indices]
        )

    return (
        mean_forecast_by_bin, 
        mean_observation_by_bin, 
        num_examples_by_bin,
    )

_get_histogram 函数用于计算直方图数据，返回与输入数据相同的数组，每个值表示数据桶的序号。

def _get_histogram(
    input_values: np.ndarray, 
    num_bins: int, 
    min_value: float, 
    max_value: float,
) -> np.array:
    bin_cutoffs = np.linspace(
        min_value, 
        max_value, 
        num=num_bins + 1
    )

    inputs_to_bins = np.digitize(
        input_values, 
        bin_cutoffs, 
        right=False
    ) - 1

    inputs_to_bins[inputs_to_bins < 0] = 0
    inputs_to_bins[inputs_to_bins > num_bins - 1] = num_bins - 1

    return inputs_to_bins

注：

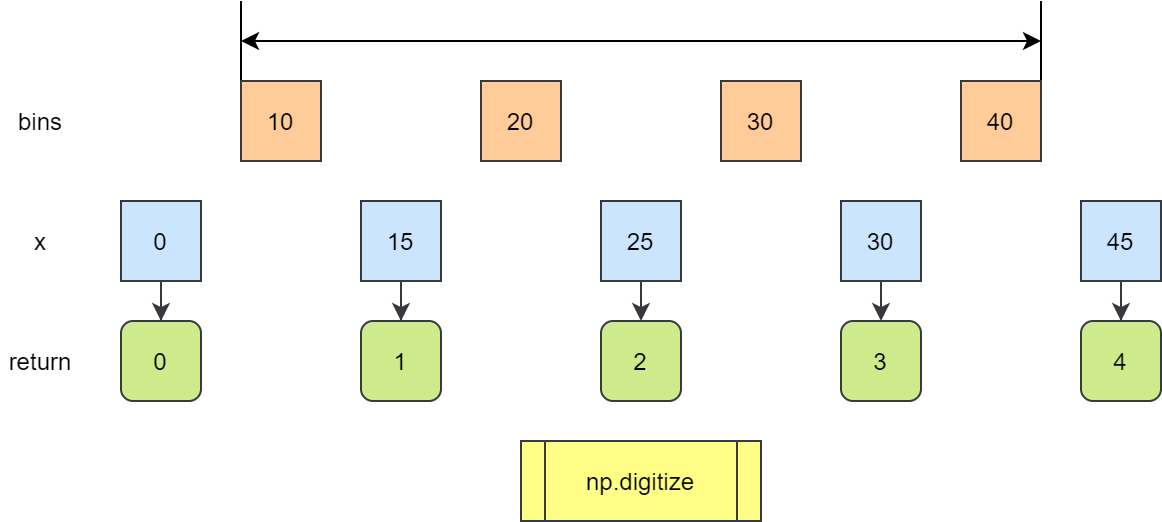
np.digitize 函数返回输入数组中每个值所属的 bin 的索引。

默认情况下 bins[i-1] <= x < bins[i]

如果 x 超过 bins 的范围，返回 0 或者 len(bins)

_plot_forecast_hist_for_regression 在可靠性曲线图中绘制右下角的直方图

def _plot_forecast_hist_for_regression(
    figure_object, 
    mean_forecast_by_bin: np.ndarray, 
    num_examples_by_bin: np.ndarray,
):
    # 每个桶的概率
    bin_frequencies = (
        num_examples_by_bin.astype(float) / np.sum(num_examples_by_bin)
    )

    num_bins = len(num_examples_by_bin)
    forecast_bin_width = (
        (np.max(mean_forecast_by_bin) - np.min(mean_forecast_by_bin)) /
        (num_bins - 1)
    )

    inset_axes_object = figure_object.add_axes([
        0.575, 
        0.225,
        0.3, 
        0.25
    ])
    
    # 绘制条形图
    inset_axes_object.bar(
        mean_forecast_by_bin, 
        bin_frequencies, 
        forecast_bin_width,
        color=np.array([228, 26, 28], dtype=float) / 255, 
        edgecolor=np.full(3, 0.),
        linewidth=2
    )
    
    # 坐标轴刻度
    max_y_tick_value = _floor_to_nearest(
        1.05 * np.max(bin_frequencies), 
        0.1
    )
    num_y_ticks = 1 + int(np.round(
        max_y_tick_value / 0.1
    ))

    y_tick_values = np.linspace(
        0, max_y_tick_value, 
        num=num_y_ticks
    )
    pyplot.yticks(
        y_tick_values, 
        axes=inset_axes_object)
    pyplot.xticks(
        np.linspace(0, 0.02, num=11), 
        axes=inset_axes_object,
        rotation=90.
    )
    
    # 坐标轴范围
    inset_axes_object.set_xlim(
        0, 
        np.max(mean_forecast_by_bin) + forecast_bin_width
    )
    inset_axes_object.set_ylim(
        0, 
        1.05 * np.max(bin_frequencies)
    )

_floor_to_nearest 将数字向下舍入到 increment 的最近倍数

def _floor_to_nearest(
    input_value_or_array, 
    increment,
):
    return increment * np.floor(input_value_or_array / increment)

绘制可靠性曲线

训练集

_ = evaluate_regression(
    target_values=training_target_table[TARGET_NAME].values,
    predicted_target_values=training_predictions,
    mean_training_target_value=mean_training_target_value,
    dataset_name='training'
)

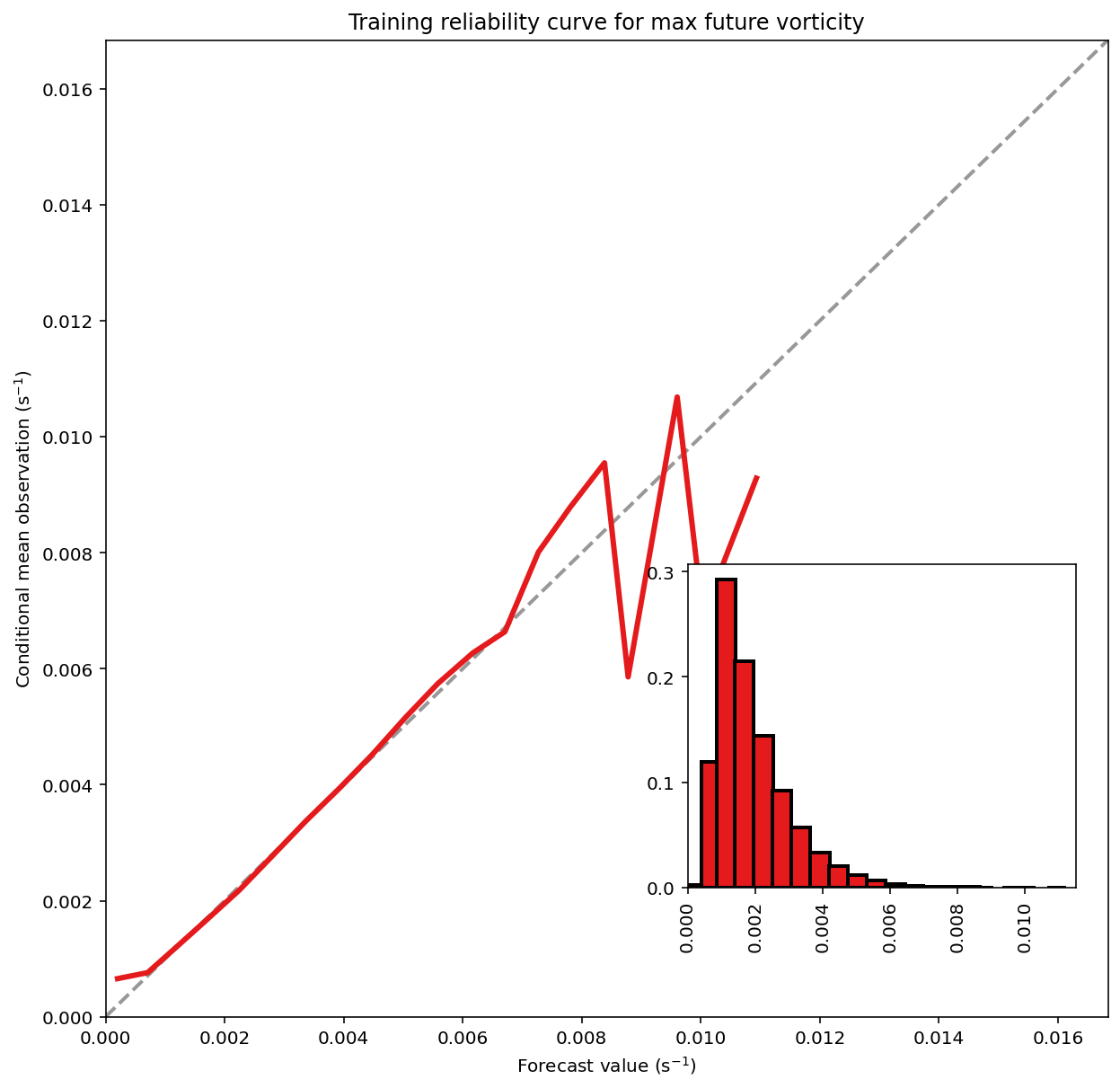
Training MAE (mean absolute error) = 7.714e-04 s^-1
Training MSE (mean squared error) = 1.112e-06 s^-2
Training bias (mean signed error) = 1.846e-19 s^-1
Training MAE skill score (improvement over climatology) = 0.315
Training MSE skill score (improvement over climatology) = 0.521

验证集

validation_predictions = linreg_model_object.predict(
    validation_predictor_table.values
)

_ = evaluate_regression(
    target_values=validation_target_table[TARGET_NAME].values,
    predicted_target_values=validation_predictions,
    mean_training_target_value=mean_training_target_value,
    dataset_name='validation'
)

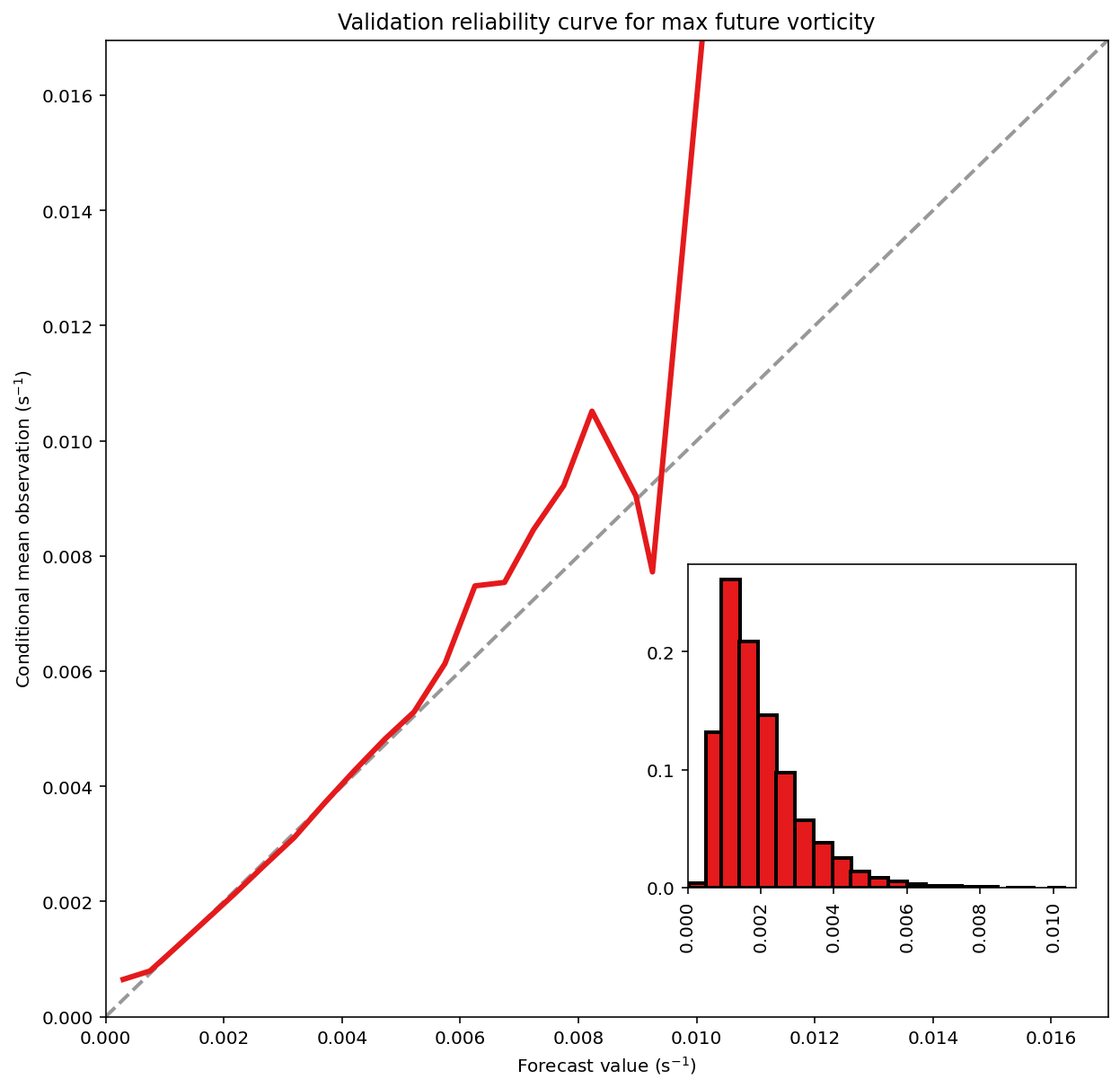
Validation MAE (mean absolute error) = 7.505e-04 s^-1
Validation MSE (mean squared error) = 1.048e-06 s^-2
Validation bias (mean signed error) = -9.007e-07 s^-1
Validation MAE skill score (improvement over climatology) = 0.316
Validation MSE skill score (improvement over climatology) = 0.540

线性回归：系数

下一个单元将为线性回归模型绘制系数。如果预测变量 x_{j} 具有正（负）系数，则预测值随着 x_{j} 增大（减小）。

请记住，所有预测变量均已归一化为相同的标度（z-score），因此通常具有较大系数的预测变量更为重要。

另外，请注意，模型使用了每个预测变量（系数为非零）。

使用到的函数

def plot_model_coefficients(
    model, 
    predictor_names
):
    # 获取系数
    coefficients = model.coef_
    num_dimensions = len(coefficients.shape)
    if num_dimensions > 1:
        coefficients = coefficients[0, ...]
    
    # 根据输入变量数确定 y 轴坐标
    num_predictors = len(predictor_names)
    y_coords = np.linspace(
        0, 
        num_predictors - 1, 
        num=num_predictors, 
        dtype=float
    )

    _, axes_object = pyplot.subplots(
        1, 1, 
        figsize=(10, 10)
    )
    
    # 绘制条形图
    axes_object.barh(
        y_coords, 
        coefficients, 
        color=np.array([27, 158, 119], dtype=float) / 255,
        edgecolor=np.array([27, 158, 119], dtype=float) / 255, 
        linewidth=2
    )

    pyplot.xlabel('Coefficient')
    pyplot.ylabel('Predictor variable')

    pyplot.yticks([], [])
    x_tick_values, _ = pyplot.xticks()
    pyplot.xticks(x_tick_values, rotation=90)
    
    # 设置 x 轴范围
    x_min = np.percentile(coefficients, 1.)
    x_max = np.percentile(coefficients, 99.)
    pyplot.xlim([x_min, x_max])
    
    # 添加标签
    for j in range(num_predictors):
        axes_object.text(
            0, 
            y_coords[j], 
            predictor_names[j], 
            color=np.array([217, 95, 2], dtype=float) / 255,
            horizontalalignment='center', 
            verticalalignment='center',
            fontsize=14
        )

绘制

plot_model_coefficients(
    model=linreg_model_object,
    predictor_names=list(training_predictor_table)
)
pyplot.show()

参考

https://github.com/djgagne/ams-ml-python-course

AMS 机器学习课程

《AMS机器学习课程：数据分析与预处理》

《AMS机器学习课程：预测雷暴旋转的基础机器学习 - 数据》