统计数值天气预报模式产品生成的典型时间
在之前的文章《统计数值天气预报模式产品生成时间》中展示使用产品生成消息数据绘制逐日的产品生成情况。
其实如果文件在归档后没有改动,仅用产品文件本身也可以实现类似的功能。
本文介绍如何使用 GRIB2 文件的创建时间来统计产品生成的典型时间。
声明:本文仅代表作者个人观点,所用数据无法代表真实情况,严禁转载。关于模式系统的相关信息,请以官方发布的信息及经过同行评议的论文为准。
预先准备
首先导入需要的库。
import numpy as np
import pandas as pd文件创建时间
Linux 中文件的创建时间等于修改时间,本文假定产品文件在生成后不会被修改。
下面的代码将获取文件修改时间,返回 pandas.Timestamp 格式,其中 f 是文件路径。
from pathlib import Path
created_time = pd.to_datetime(Path(f).stat().st_mtime_ns)获取单个时效的数据
本文统计 3 月 1 日到 3 月 31 日共一个月的 GRIB 2 文件创建时间。
下面使用nwpc-oper/nwpc-data获取 MODEL A 的3月份逐日 00 时次 000 时效的 GRIB 2 文件路径。并使用上面的代码获取文件创建时间,并减去对应的日期,返回 pandas.Timedelta 对象。
from nwpc_data.data_finder import find_local_file
date_range = pd.date_range("2020-03-01 00:00:00", "2020-03-31 00:00:00", freq="D")
file_list=[
find_local_file(
"model_A/grib2/orig",
start_time=t,
forecast_time="0h"
)
for t
in date_range
]
ts = [pd.to_datetime(Path(f).stat().st_mtime_ns) - d for f, d in zip(file_list, date_range) ]
s = pd.Series(ts, index=date_range)
s2020-03-01 04:12:38
2020-03-02 04:16:45
2020-03-03 04:16:48
2020-03-04 04:37:14
2020-03-05 04:19:14
2020-03-06 04:24:41
2020-03-07 04:16:53
2020-03-08 04:20:53
2020-03-09 04:20:38
2020-03-10 04:22:12
2020-03-11 04:17:40
2020-03-12 04:19:38
2020-03-13 04:18:30
2020-03-14 04:19:57
2020-03-15 04:18:08
2020-03-16 04:18:40
2020-03-17 04:26:59
2020-03-18 04:19:53
2020-03-19 04:21:08
2020-03-20 04:22:10
2020-03-21 04:22:52
2020-03-22 04:17:04
2020-03-23 04:24:48
2020-03-24 04:25:38
2020-03-25 04:20:53
2020-03-26 04:21:02
2020-03-27 05:31:12
2020-03-28 04:20:12
2020-03-29 04:18:17
2020-03-30 04:21:32
2020-03-31 04:22:06
Freq: D, dtype: timedelta64[ns]
探索数据
使用 Bokeh 绘制 000 时效文件生成时间的折线。
from bokeh.io import output_notebook, show
from bokeh.plotting import figure
output_notebook()
data = s
p = figure(
plot_width=1000,
plot_height=600,
y_axis_type="datetime",
x_axis_type="datetime",
title="MODEL A GRIB2 ORIG forecast 000h"
)
l = p.line(
data.index,
data,
line_color="blue",
)
p.xaxis.axis_label = "date"
p.yaxis.axis_label = "clock"
show(p)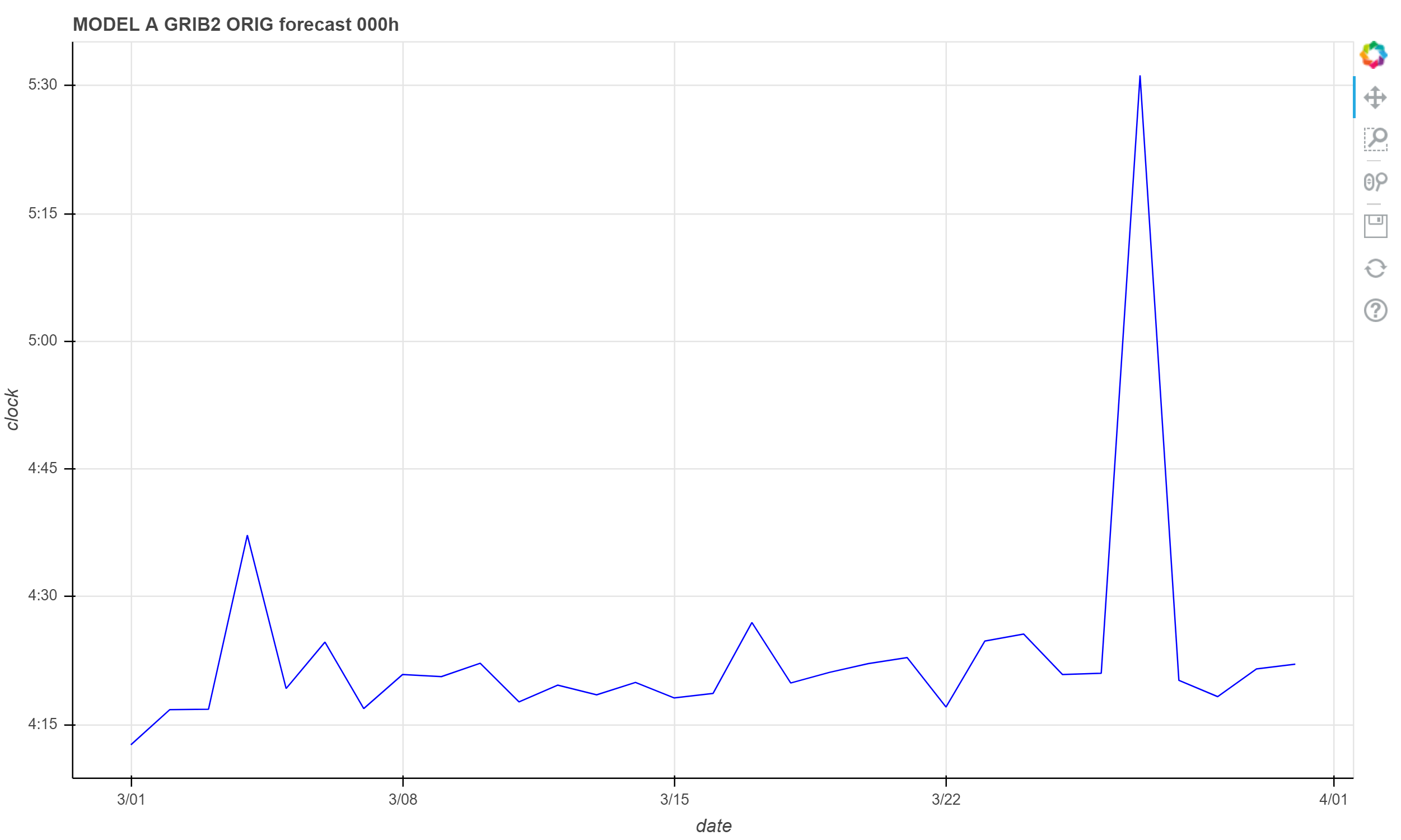
MODEL A 00 时次 000 时效 GRIB 2 ORIG 文件生成时间
可以看到,生成时间集中在UTC 4:15 - 4:30 之间,但也有明显的离群值。
计算几个统计指标:均值、中位数、切尾均值(0.1)。
from scipy import stats
print("Mean:\t\t", s.mean().ceil("S"))
print("Median:\t\t", s.median())
print("Trimmed Mean:\t", pd.to_timedelta(stats.trim_mean(s.values, 0.1)))Mean: 0 days 04:23:07
Median: 0 days 04:20:38
Trimmed Mean: 0 days 04:20:36
可以看到受离群值影响,平均值比中位数大。切尾均值和中位数比较接近。
参考切尾均值的算法,去掉前后各10%的数据,再计算标准差。
count = len(s)
trimmed_s = s.sort_values()[int(count*0.1):int(count*0.9)]
print(trimmed_s.mean())
print(trimmed_s.std())0 days 04:20:22.541666
0 days 00:02:08.450287
可以看到,均值与切尾均值的差值已超过上面计算的标准差。 所以如果想要正常情况下产品生成的典型时间,可以使用切尾均值。
获取整个时效的数据
将上面的方法扩展到整个时效,下面的函数返回时间段内各个时效完成时间的表格数据。
def calculate_time(
data_type,
date_range,
forecast_hours,
):
b = []
for forecast_hour in forecast_hours:
file_list=[
find_local_file(
data_type,
start_time=t,
forecast_time=forecast_hour
)
for t
in date_range
]
ts = [pd.to_datetime(Path(f).stat().st_mtime_ns) - d for f, d in zip(file_list, date_range) ]
s = pd.Series(ts, index=date_range)
s.name = int(forecast_hour.seconds/3600) + forecast_hour.days * 24
b.append(s)
df = pd.DataFrame(b)
df = df.T
return df下面获取 MODEL A 00 时次的数据。
起报时间和预报时效列表
date_range = pd.date_range("2020-03-01 00:00:00", "2020-03-31 00:00:00", freq="D")
forecast_hours = [pd.Timedelta(hours=h) for h in np.append(np.arange(0, 121, 3), np.arange(126, 241, 6))]计算时间
df = calculate_time("model_A/grib2/orig", date_range, forecast_hours)
df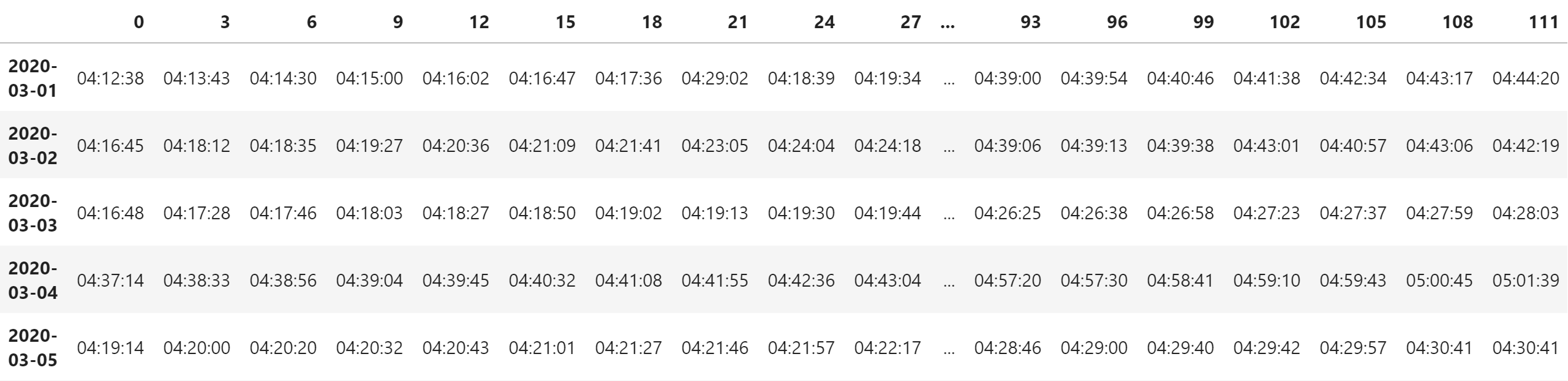
MODEL A 00 时次 GRIB 2 ORIG 文件生成时间表格
计算每个时效的统计指标,包括均值、中位数、切尾均值(0.1)、四分位数。
stat_df = pd.DataFrame(
{
"mean": df.mean(),
"median": df.median(),
"trim_mean": df.apply(lambda x: pd.to_timedelta(stats.trim_mean(x.values, 0.1))),
"1/4": df.quantile(.25, numeric_only=False),
"3/4": df.quantile(.75, numeric_only=False),
}
)
stat_df = stat_df.applymap(lambda x: x.ceil("S"))
stat_df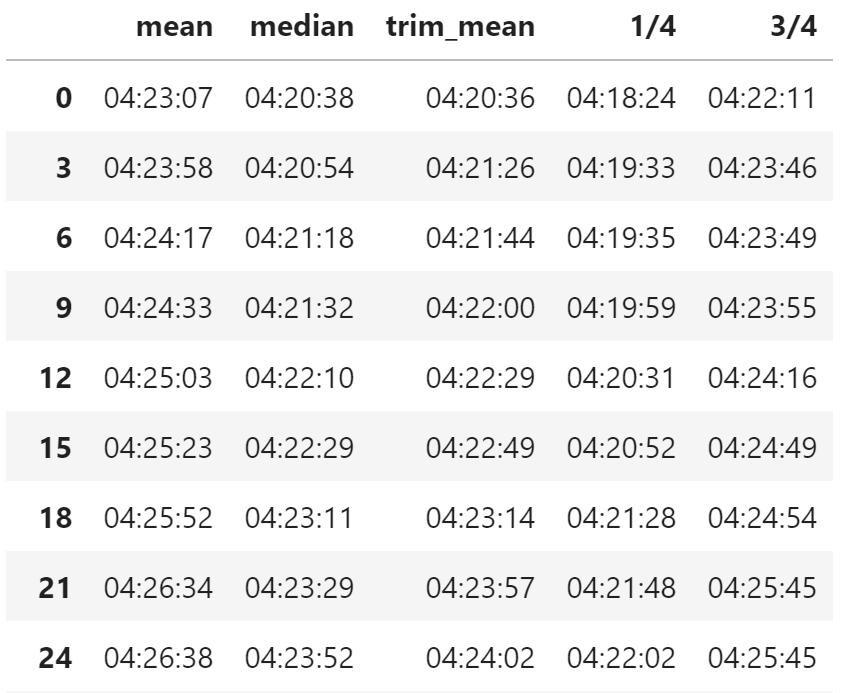
MODEL A 00 时次 GRIB 2 ORIG 文件生成时间统计表格
为了更清晰地展示各个统计量,使用 Bokeh 画图。
data = stat_df
p = figure(
plot_width=1000,
plot_height=600,
y_axis_type="datetime",
title="MODEL A GRIB2 ORIG",
)
p.yaxis.formatter = DatetimeTickFormatter(
minsec=['%H:%M:%S'],
minutes=['%H:%M:%S'],
hourmin=['%H:%M:%S'],
hours=['%H:%M:%S']
)
p.line(
data.index,
data['mean'],
line_color="SkyBlue",
legend_label="mean",
)
p.line(
data.index,
data['trim_mean'],
line_color="Salmon",
legend_label="tmean(0.1)",
)
p.line(
data.index,
data['1/4'],
line_color="Pink",
legend_label="1/4",
)
p.line(
data.index,
data['median'],
line_color="green",
legend_label="1/2",
)
p.line(
data.index,
data['3/4'],
line_color="Purple",
legend_label="3/4",
)
p.xaxis.axis_label = "forecast hour"
p.yaxis.axis_label = "clock"
p.legend.location = "top_left"
show(p)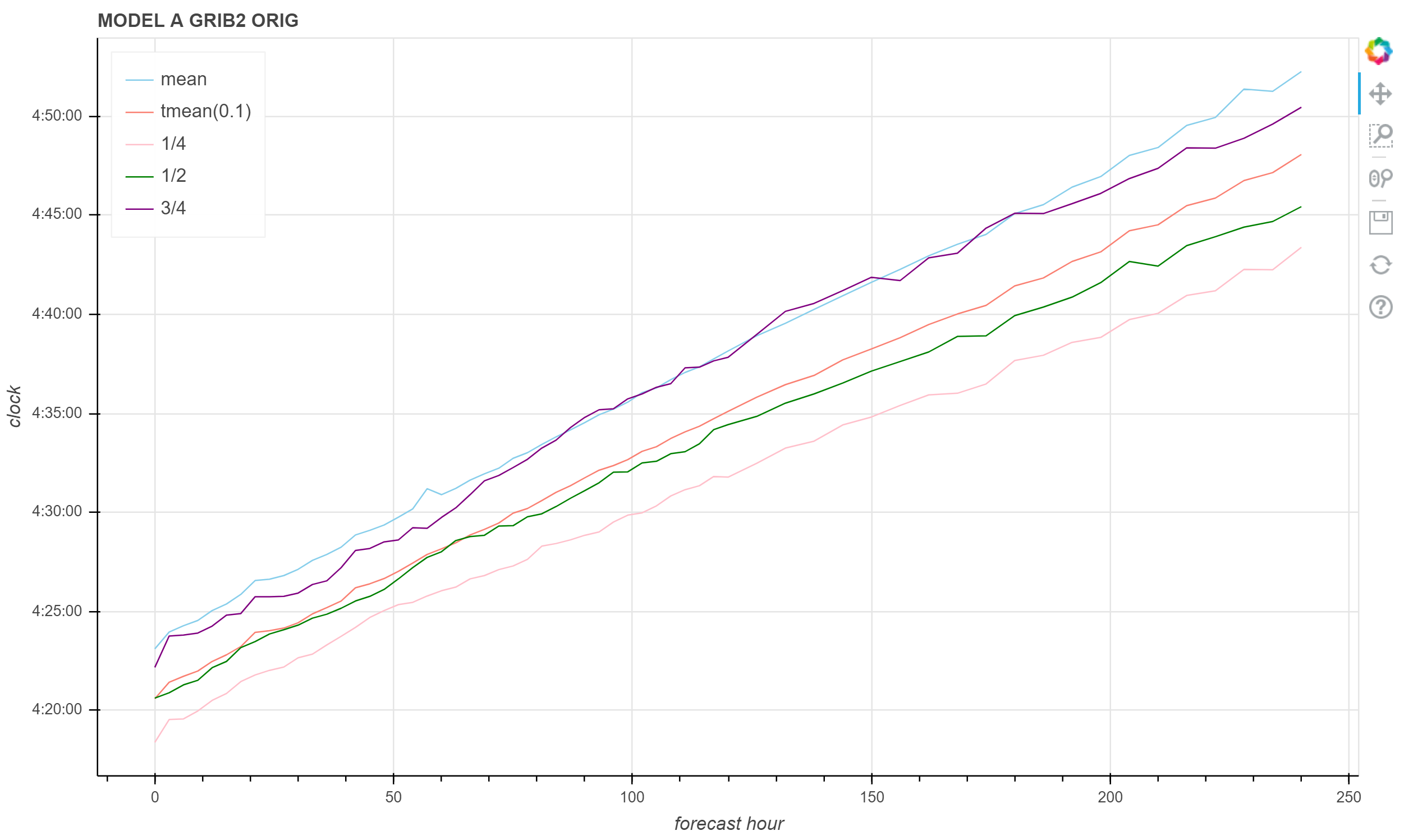
MODEL A 00 时次 GRIB 2 ORIG 文件生成时间统计图
可以看到均值几乎大于75分位数,而中位数和切尾均值相差不大。 所以建议使用切尾均值作为产品生成时间的典型值。
更多示例
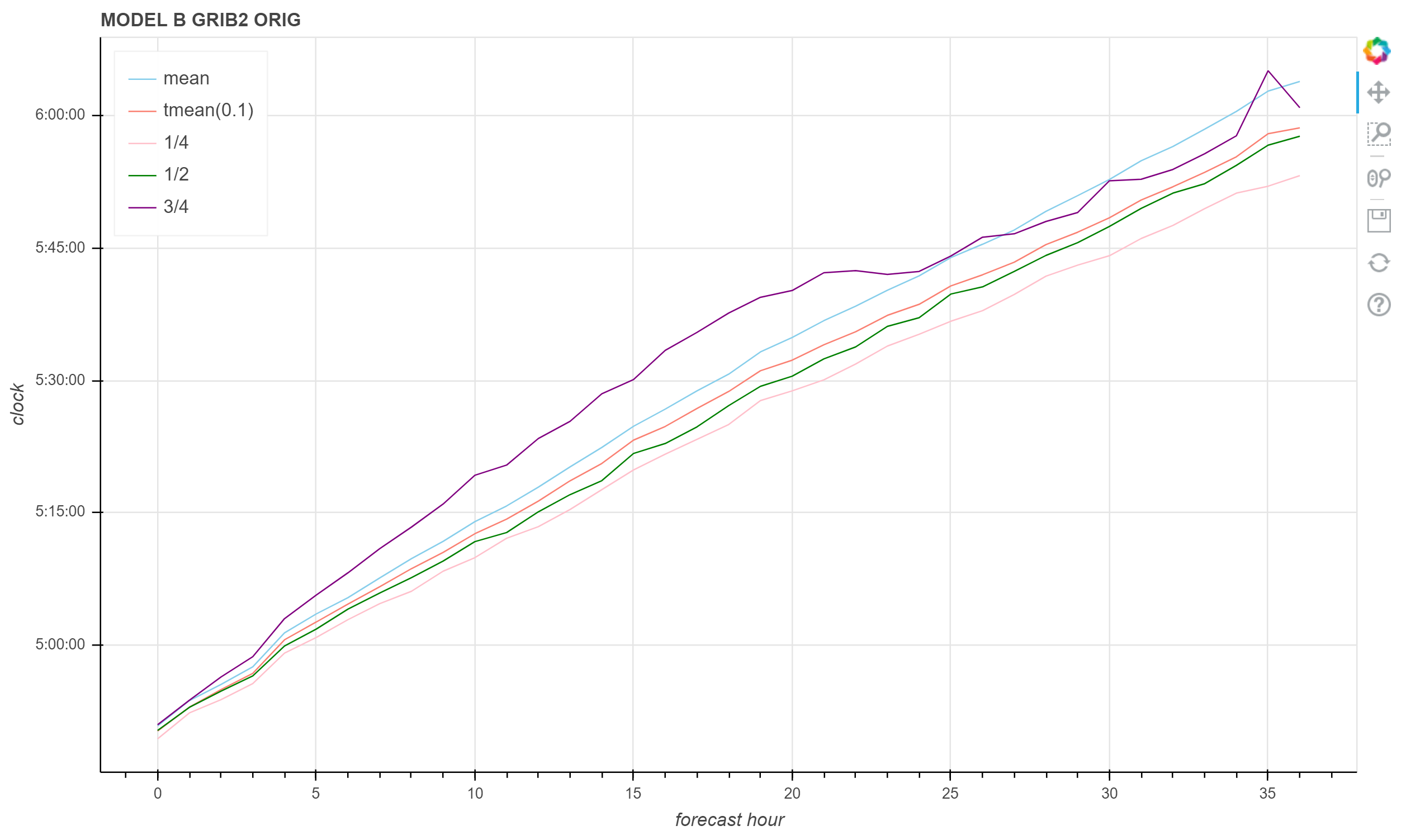
MODEL B 00 时次 GRIB 2 ORIG 文件生成时间统计图
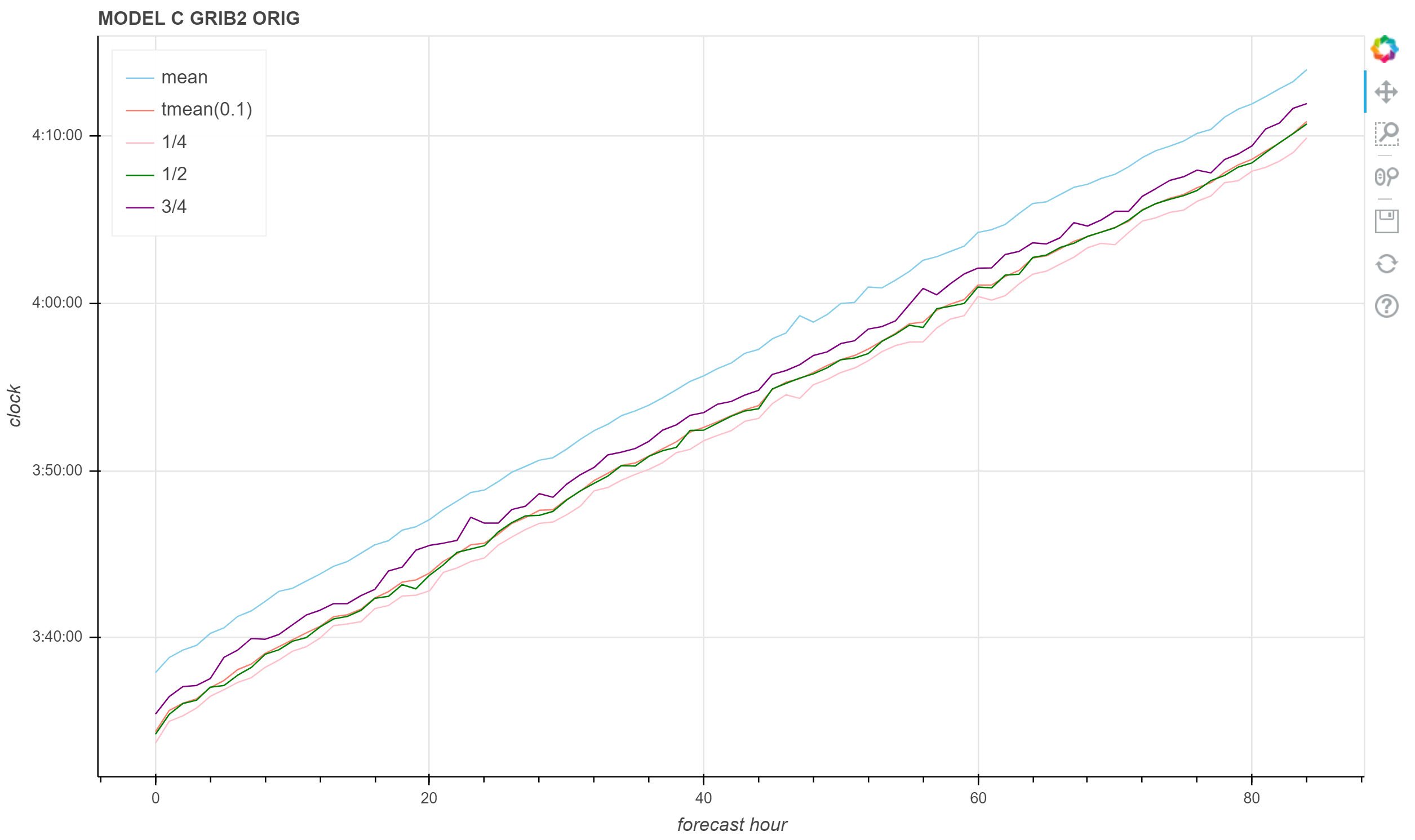
MODEL C 00 时次 GRIB 2 ORIG 文件生成时间统计图
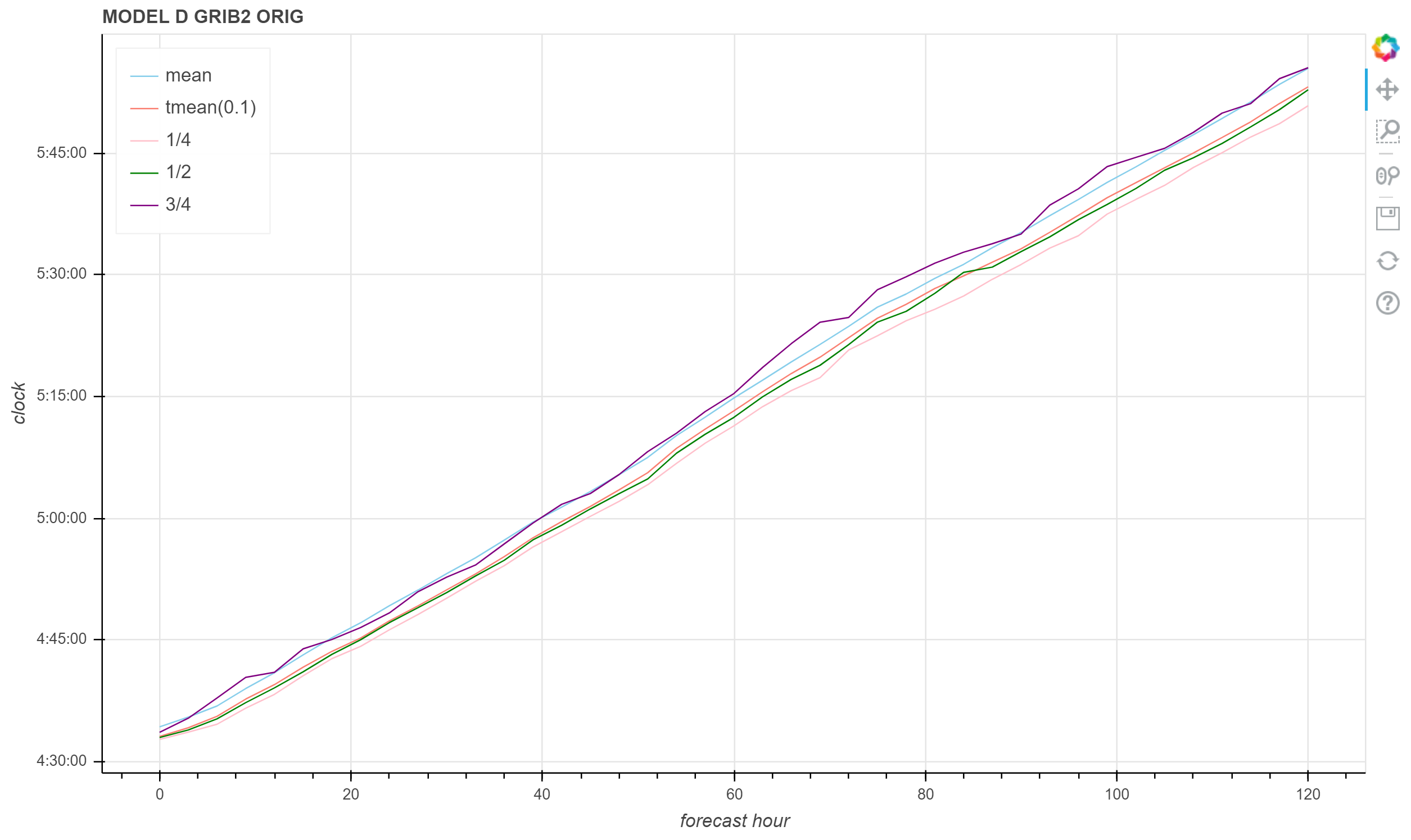
MODEL D 00 时次 GRIB 2 ORIG 文件生成时间统计图
上述三个示例中,切尾均值与中位数保持同样的关系。
参考
更新
2010.04.19:《Bokeh教程:添加标注》介绍如何添加标注,并展示更新后的绘图结果。
