WeatherBench:创建线性回归模型
本文来自 weatherbench 项目源码:
https://github.com/pangeo-data/WeatherBench/blob/master/notebooks/2-linear-regression-baseline.ipynb
在这个笔记本中,我们将创建线性回归基线模型
准备
import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
import seaborn as sns
import pickle
# from src.score import *
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from tqdm import tqdm_notebook as tqdm
sns.set_style('darkgrid')
sns.set_context('notebook')
def to_pickle(obj, fn):
with open(fn, 'wb') as f:
pickle.dump(obj, f)
def read_pickle(fn):
with open(fn, 'rb') as f:
return pickle.load(f)
为训练加载和准备数据
首先,我们需要加载和准备数据。 这样我们可以将其馈入到我们的线性回归模型中
data_dir = '/g11/wangdp/data/weather-bench/5.625deg'
baseline_dir = '/g11/wangdp/data/weather-bench/baselines-wangdp'
加载相关变量的整个数据集,包括:
- 500hPa 位势高度
- 850hPa 温度
- 6 小时累计降水
- 2 米温度
z500 = xr.open_mfdataset(
f'{data_dir}/geopotential_500/*.nc',
combine='by_coords'
).z.drop('level')
t850 = xr.open_mfdataset(
f'{data_dir}/temperature_850/*.nc',
combine='by_coords'
).t.drop('level')
tp = xr.open_mfdataset(
f'{data_dir}/total_precipitation/*.nc',
combine='by_coords'
).tp.rolling(time=6).sum()
tp.name = 'tp'
t2m = xr.open_mfdataset(
f'{data_dir}/2m_temperature/*.nc',
combine='by_coords'
).t2m
合并为一个数据集。
包括 3 个维度:
- 时间:1979.01.01 00:00 - 2018.12.31 23:00,逐小时间隔
- 纬度:-87.1875 - 87.1875,共 32 个
- 经度:0 - 354.375,共 64 个
包括 4 个变量:
- z
- t
- tip
- t2m
data = xr.merge([
z500,
t850,
tp,
t2m
])
data
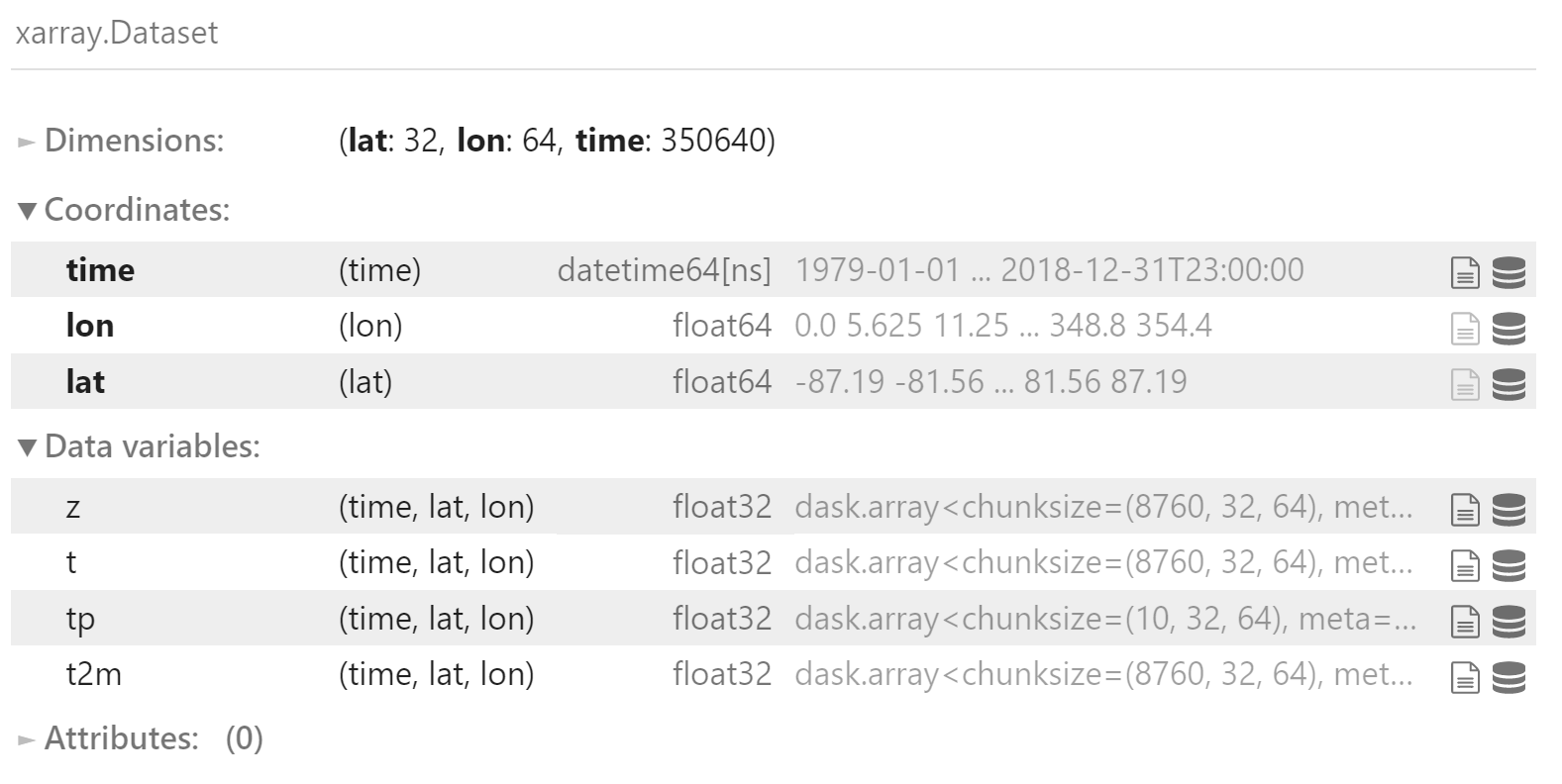
加载验证集:2017 和 2018 年
load_test_data() 函数用于加载某个要素的验证集
def load_test_data(path, var, years=slice('2017', '2018')):
ds = xr.open_mfdataset(f'{path}/*.nc', combine='by_coords')[var]
if var in ['z', 't']:
try:
ds = ds.sel(
level=500 if var == 'z' else 850
).drop('level')
except ValueError:
ds = ds.drop('level')
return ds.sel(time=years)
加载多个要素的验证集
z500_test = load_test_data(
f'{data_dir}/geopotential_500', 'z'
)
t850_test = load_test_data(
f'{data_dir}/temperature_850', 't'
)
tp_test = load_test_data(
f'{data_dir}/total_precipitation', 'tp'
).rolling(time=6).sum()
tp_test.name = 'tp'
t2m_test = load_test_data(
f'{data_dir}/2m_temperature', 't2m'
)
合并验证集
test_data = xr.merge([
z500_test,
t850_test,
tp_test,
t2m_test
])
test_data
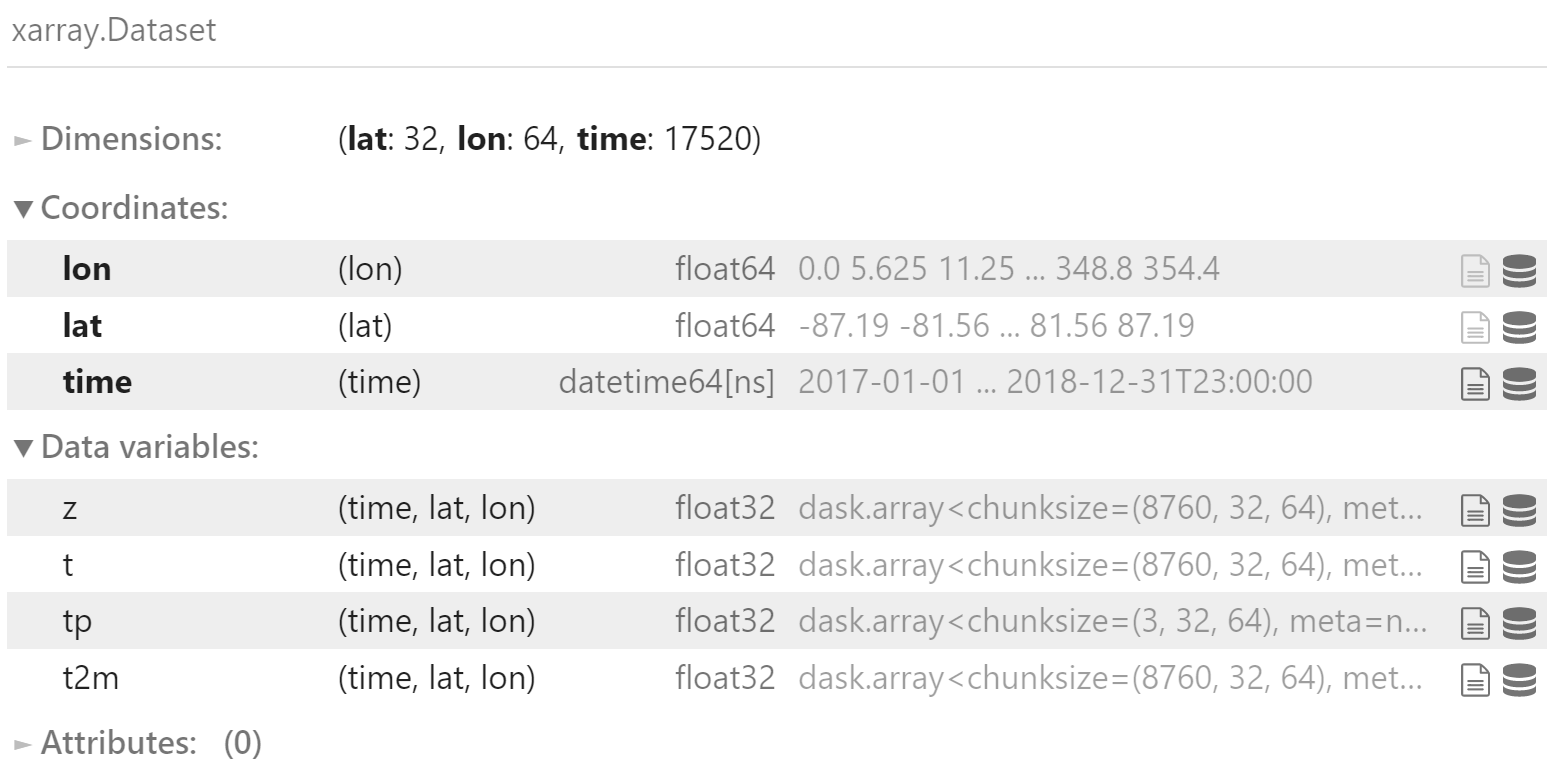
6 小时累计降水数据 (tp) 缺失前面 7 + 6 个值,所以从 7 + 6 数据开始
注:前 12 个值为空 (?)
data.tp[:6+7+1].mean(('lat', 'lon')).compute()
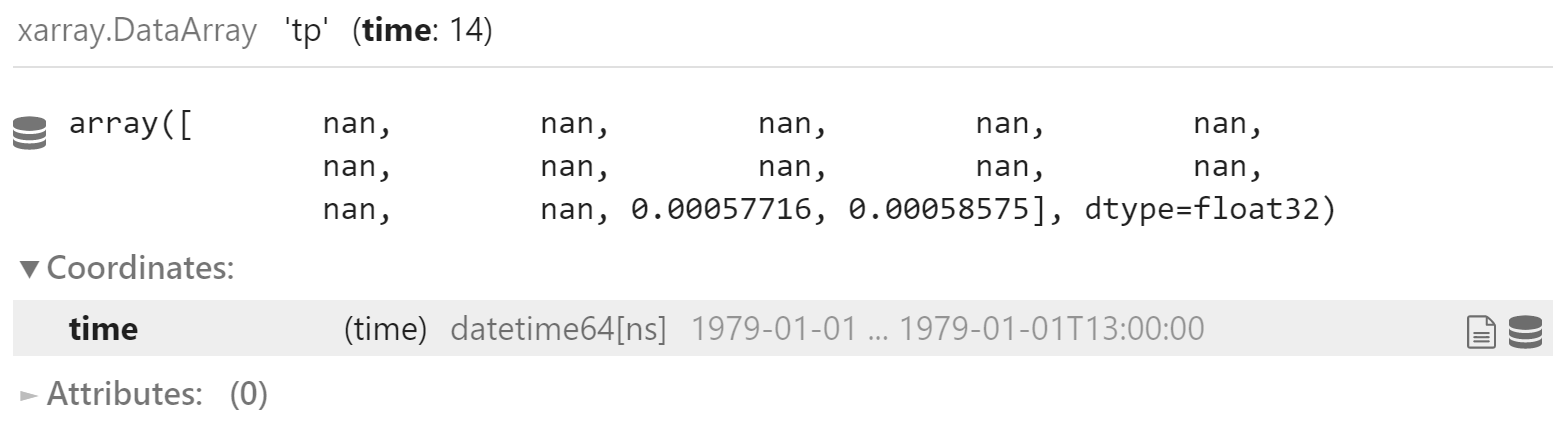
data = data.isel(
time=slice(7+6, None)
)
data
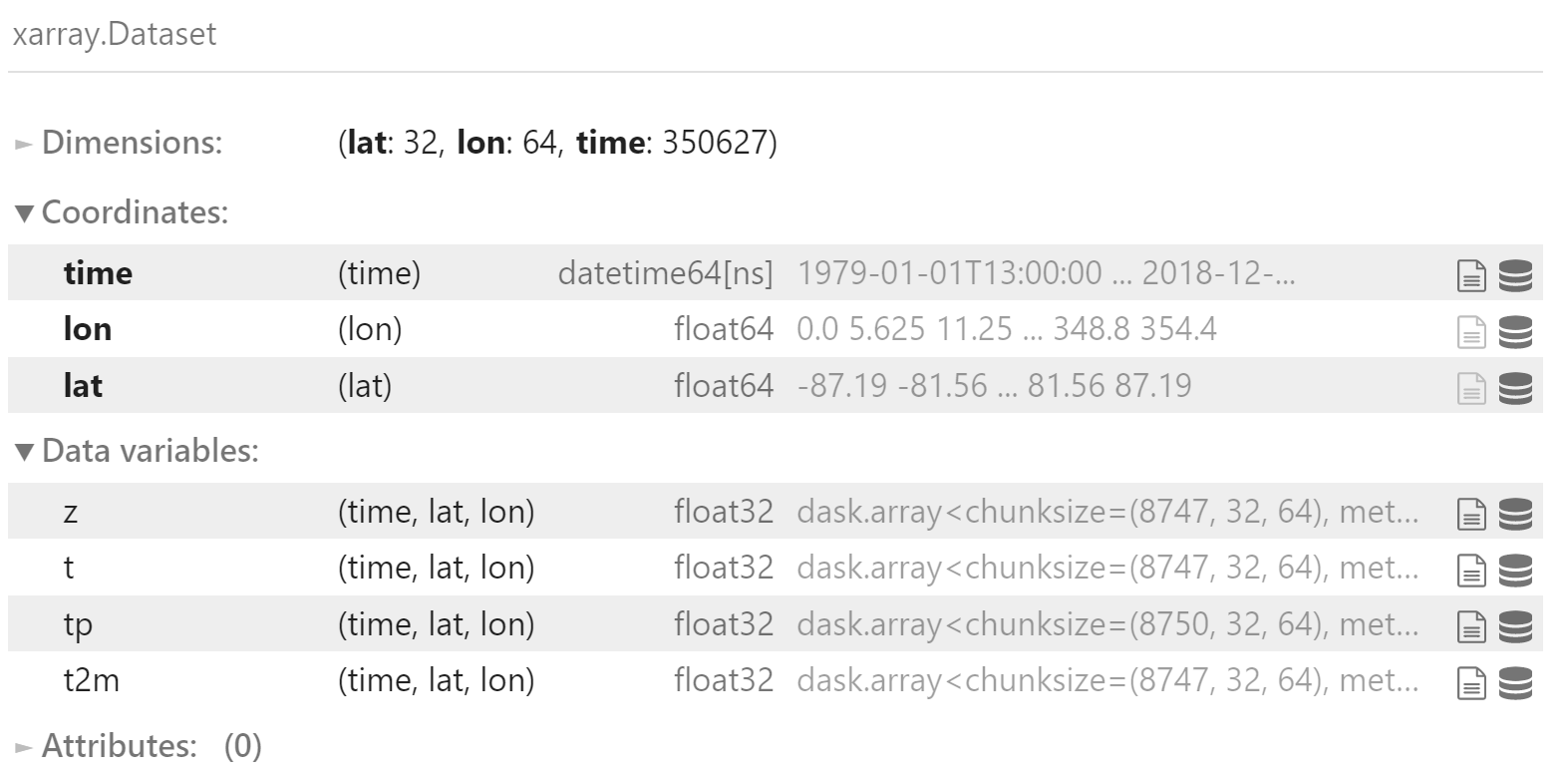
训练集和测试集
将数据分成训练集和测试集。
是的,从技术上讲,我们应该有一个单独的验证集,但对于线性回归而言,这并不重要。
data_train = data.sel(time=slice('1979', '2016'))
data_test = data.sel(time=slice('2017', '2018'))
归一化
计算训练集的归一化统计
注意:这里仅选取时间维度的一部分样本数据,加快计算速度
data_mean = data_train.isel(
time=slice(0, None, 10000)
).mean().load()
data_std = data_train.isel(
time=slice(0, None, 10000)
).std().load()
使用相同的参数归一化训练集和测试集
data_train = (data_train - data_mean) / data_std
data_test = (data_test - data_mean) / data_std
可视化
查看归一化后的数据集
网格大小是 32*64
_, nlat, nlon = data_train.z.shape
nlat, nlon
(32, 64)
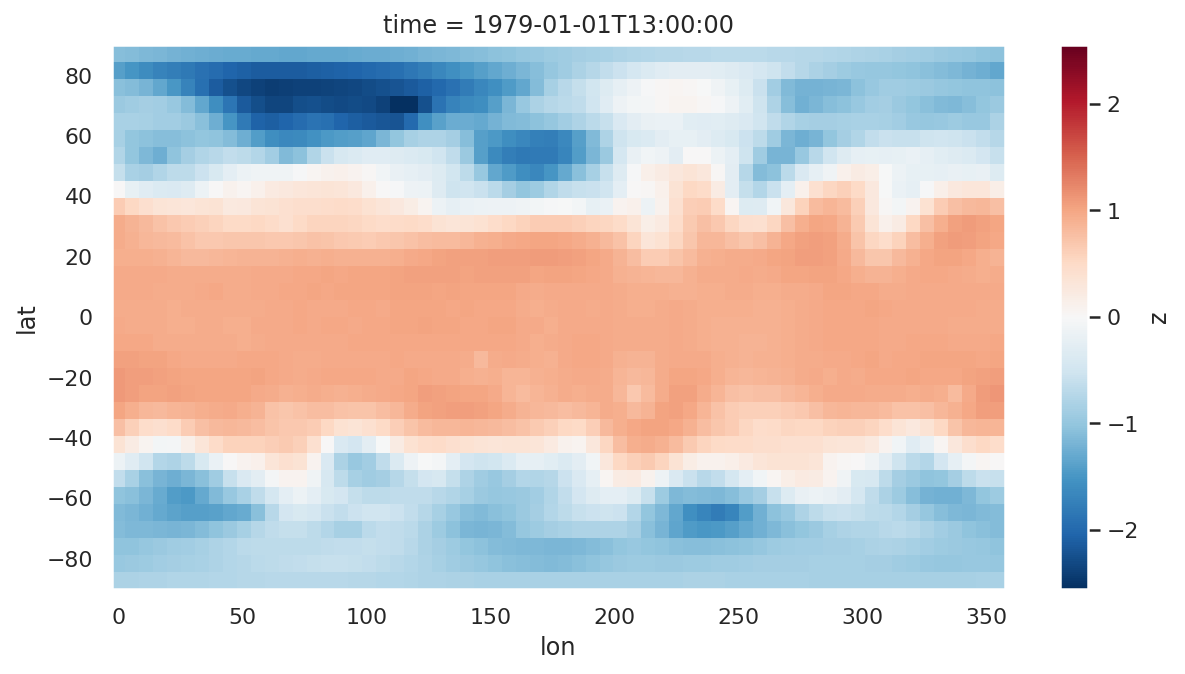
绘制 500hPa 位势高度
data_train.z.isel(time=0).plot(
aspect=2,
size=5
)
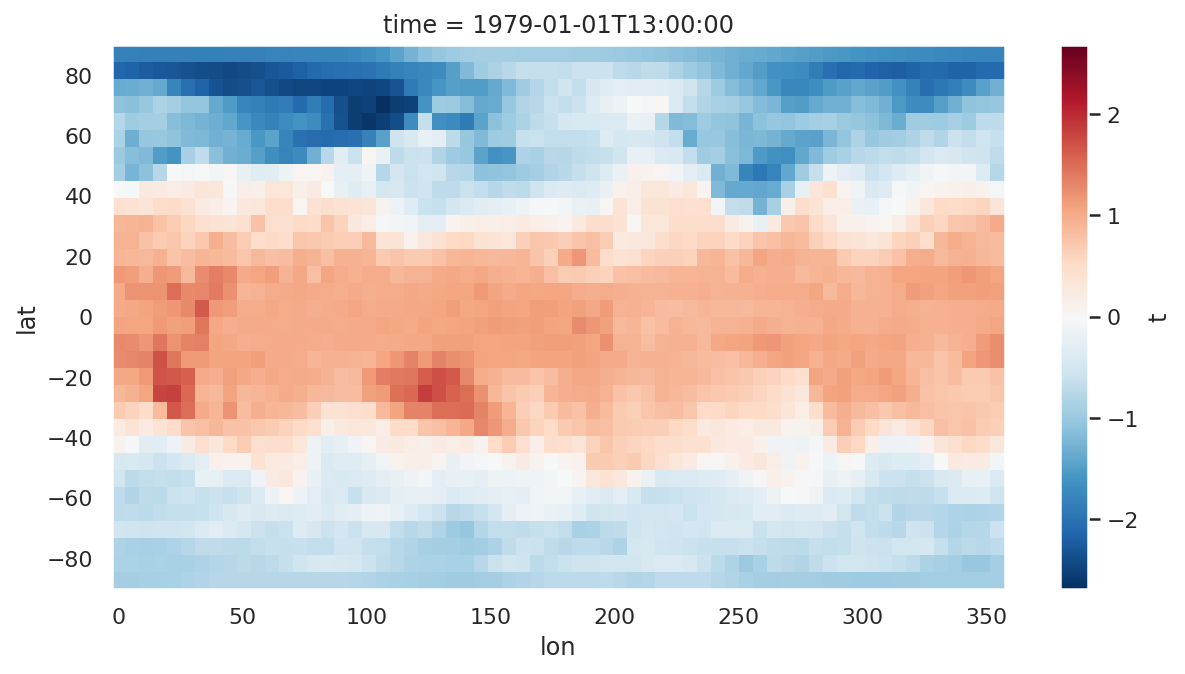
绘制 850hPa 温度场
data_train.t.isel(time=0).plot(
aspect=2,
size=5
)
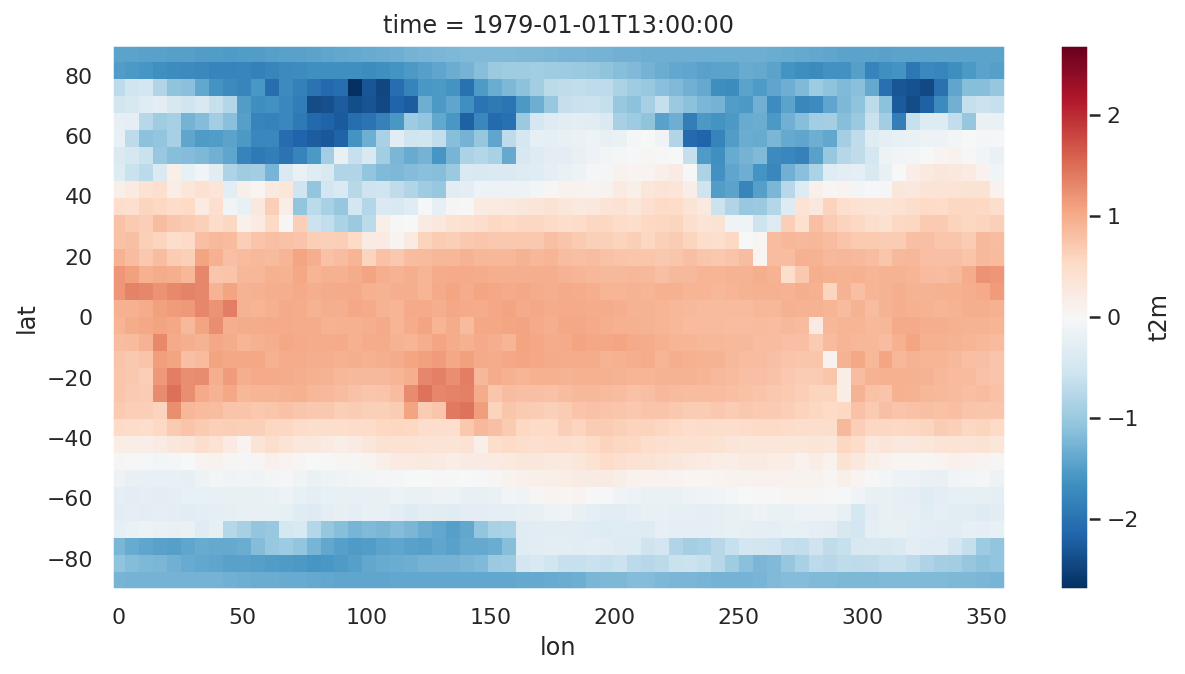
绘制 2m 温度场
data_train.t2m.isel(time=0).plot(
aspect=2,
size=5
)
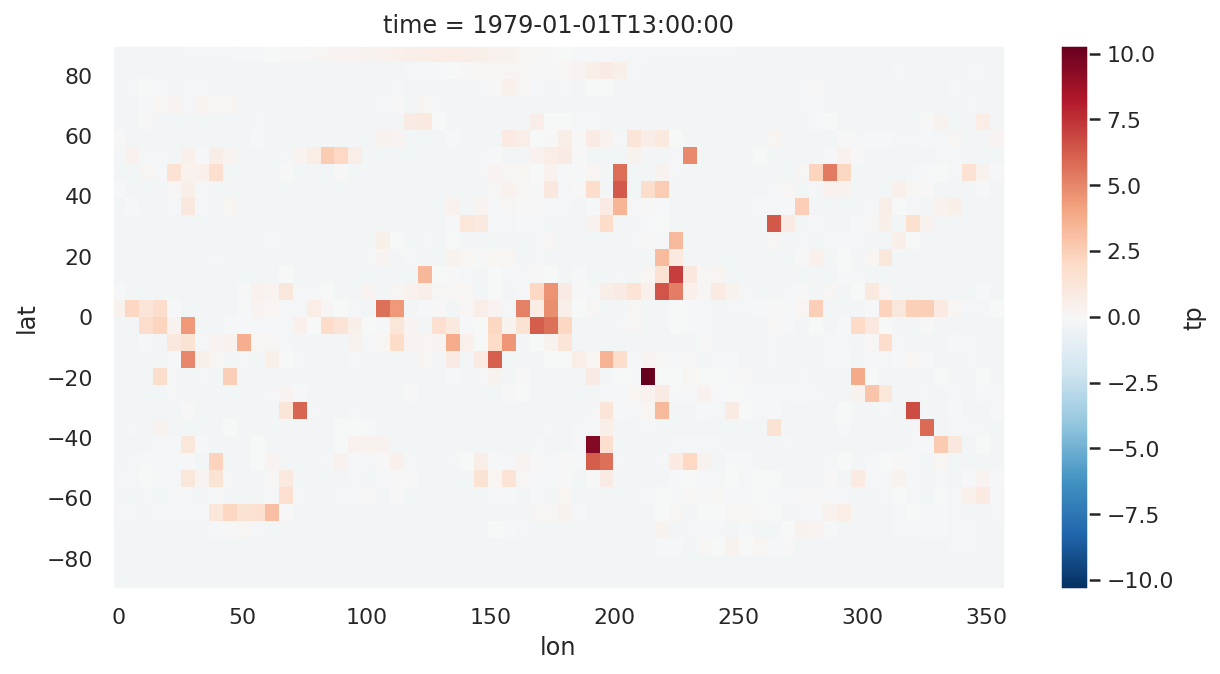
绘制 6 小时累计降水
data_train.tp.isel(time=0).plot(
aspect=2,
size=5
)
训练数据集
data_train
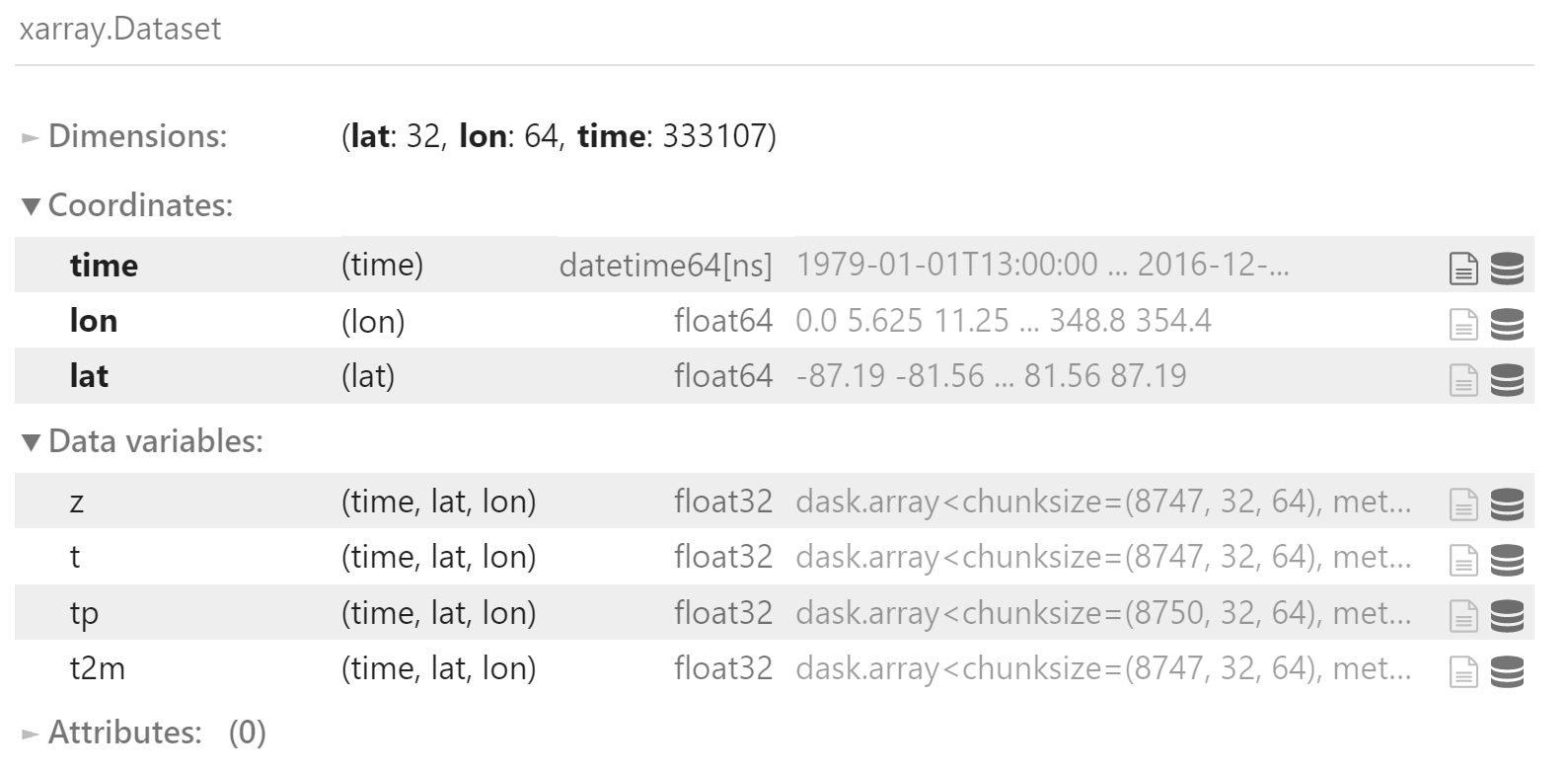
create_training_data() 函数根据预报时长将数据分为输入数据和输出数据
注:本例中输入和输出使用相同的数据源,区别仅在于对数据的切分
def create_training_data(
da,
lead_time_h,
return_valid_time=False
):
"""Function to split input and output by lead time."""
X = da.isel(time=slice(0, -lead_time_h))
y = da.isel(time=slice(lead_time_h, None))
valid_time = y.time
if return_valid_time:
return X.values.reshape(-1, nlat*nlon), y.values.reshape(-1, nlat*nlon), valid_time
else:
return X.values.reshape(-1, nlat*nlon), y.values.reshape(-1, nlat*nlon)
训练线性回归
现在让我们训练模型。 我们将使用 scikit-learn 实现。
train_lr() 函数创建数据集,训练一个线性回归模型 (LinearRegression),并返回预测结果
def train_lr(
lead_time_h,
input_vars,
output_vars,
data_subsample=1
):
X_train, y_train, X_test, y_test = [], [], [], []
for v in input_vars:
# 训练集
X, y = create_training_data(
data_train[v],
lead_time_h
)
X_train.append(X)
if v in output_vars: y_train.append(y)
# 测试集
X, y, valid_time = create_training_data(
data_test[v],
lead_time_h,
return_valid_time=True
)
X_test.append(X)
if v in output_vars: y_test.append(y)
X_train, y_train, X_test, y_test = [
np.concatenate(d, 1)
for d in [X_train, y_train, X_test, y_test]
]
# 数据采样,间隔 data_subsample
X_train = X_train[::data_subsample]
y_train = y_train[::data_subsample]
# 训练模型
lr = LinearRegression(n_jobs=16)
lr.fit(X_train, y_train)
# 计算均方根误差
mse_train = mean_squared_error(y_train, lr.predict(X_train))
mse_test = mean_squared_error(y_test, lr.predict(X_test))
print(f'Train MSE = {mse_train}'); print(f'Test MSE = {mse_test}')
# 计算预测值
preds = lr.predict(X_test).reshape((-1, len(output_vars), nlat, nlon))
# 使用归一化参数恢复实际值
fcs = []
for i, v in enumerate(output_vars):
fc = xr.DataArray(
preds[:, i] * data_std[v].values + data_mean[v].values,
dims=['time', 'lat', 'lon'],
coords={
'time': valid_time,
'lat': data_train.lat,
'lon': data_train.lon
},
name=v
)
fcs.append(fc)
return xr.merge(fcs), lr
3 天预报
这里我们训练一个可以直接预测 3 天预报的模型。 让我们训练一个仅预测 z500 或 t850 的模型,然后再训练一个组合模型。 正如我们在下面看到的,仅在 z500 上训练的模型比组合模型表现更好。 但是 t850 并非如此。 对于本文,我们将使用组合模型。
experiments = [
[['z'], ['z']],
[['t'], ['t']],
[['z', 't'], ['z', 't']],
[['tp'], ['tp']],
[['z', 't', 'tp'], ['tp']],
[['t2m'], ['t2m']],
[['z', 't', 't2m'], ['t2m']],
]
compute_weighted_rmse() 函数计算权重 RMSE
注:da_fc 预报数据的时间维度必须是预报时刻 (validation time)
def compute_weighted_rmse(
da_fc,
da_true,
mean_dims=xr.ALL_DIMS
):
error = da_fc - da_true
weights_lat = np.cos(np.deg2rad(error.lat))
weights_lat /= weights_lat.mean()
rmse = np.sqrt(((error)**2 * weights_lat).mean(mean_dims))
return rmse
由于对线性回归进行完整数据训练会占用大量内存,因此我们仅每 5 步执行一次,可以得出几乎相同的结果 (相差 <0.5%)
data_subsample = 5
lead_time = 3*24
preds = []
models = []
for n, (i, o) in enumerate(experiments):
print(f'{n}: Input variables = {i}; output variables = {o}')
p, m = train_lr(
lead_time,
input_vars=i,
output_vars=o,
data_subsample=data_subsample
)
preds.append(p)
models.append(m)
r = compute_weighted_rmse(p, test_data).compute()
print('; '.join([f'{v} = {r[v].values}' for v in r]) + '\n')
# 保存预测结果
p.to_netcdf(f'{baseline_dir}/lr_3d_{"_".join(i)}_{"_".join(o)}.nc')
# 保存训练过的模型
to_pickle(m, f'{baseline_dir}/saved_models/lr_3d_{"_".join(i)}_{"_".join(o)}.pkl')
0: Input variables = ['z']; output variables = ['z']
Train MSE = 0.047421738505363464
Test MSE = 0.05775298923254013
z = 693.291563560166
1: Input variables = ['t']; output variables = ['t']
Train MSE = 0.041756242513656616
Test MSE = 0.051743511110544205
t = 3.191932824832273
2: Input variables = ['z', 't']; output variables = ['z', 't']
Train MSE = 0.03748195618391037
Test MSE = 0.056943029165267944
z = 714.9538988573162; t = 3.189889127263336
3: Input variables = ['tp']; output variables = ['tp']
Train MSE = 0.7977886199951172
Test MSE = 1.0545696020126343
tp = 0.002328787984058573
4: Input variables = ['z', 't', 'tp']; output variables = ['tp']
Train MSE = 0.6883244514465332
Test MSE = 1.1536452770233154
tp = 0.0024336892090824473
5: Input variables = ['t2m']; output variables = ['t2m']
Train MSE = 0.01548975519835949
Test MSE = 0.019752470776438713
t2m = 2.3953879421632873
6: Input variables = ['z', 't', 't2m']; output variables = ['t2m']
Train MSE = 0.011629350483417511
Test MSE = 0.021696563810110092
t2m = 2.4925363492791224
如我们所见,由于过拟合,仅将输出变量作为输入的模型几乎总是表现得更好。
我们可以尝试像 ridge 或 lasso 这样的正则回归,这些模型的目标不是效果最好,而是要提供一个具有尽可能少的超参数的可靠基线。
5 天预报
data_subsample = 5
lead_time = 5*24
preds = []
models = []
for n, (i, o) in enumerate(experiments):
print(f'{n}: Input variables = {i}; output variables = {o}')
p, m = train_lr(
lead_time,
input_vars=i,
output_vars=o,
data_subsample=data_subsample
)
preds.append(p)
models.append(m)
r = compute_weighted_rmse(p, test_data).compute()
print('; '.join([f'{v} = {r[v].values}' for v in r]) + '\n')
p.to_netcdf(f'{baseline_dir}/lr_5d_{"_".join(i)}_{"_".join(o)}.nc');
to_pickle(m, f'{baseline_dir}/saved_models/lr_5d_{"_".join(i)}_{"_".join(o)}.pkl')
0: Input variables = ['z']; output variables = ['z']
Train MSE = 0.05985909700393677
Test MSE = 0.07377580553293228
z = 783.048635826814
1: Input variables = ['t']; output variables = ['t']
Train MSE = 0.04817841202020645
Test MSE = 0.06070048362016678
t = 3.4395298611456333
2: Input variables = ['z', 't']; output variables = ['z', 't']
Train MSE = 0.04625791311264038
Test MSE = 0.07199429720640182
z = 814.6593291375373; t = 3.522947849387816
3: Input variables = ['tp']; output variables = ['tp']
Train MSE = 0.803996205329895
Test MSE = 1.062649130821228
tp = 0.002337529694954724
4: Input variables = ['z', 't', 'tp']; output variables = ['tp']
Train MSE = 0.6962897777557373
Test MSE = 1.1725271940231323
tp = 0.0024531079046640984
5: Input variables = ['t2m']; output variables = ['t2m']
Train MSE = 0.018064960837364197
Test MSE = 0.023729272186756134
t2m = 2.604655271207735
6: Input variables = ['z', 't', 't2m']; output variables = ['t2m']
Train MSE = 0.013758879154920578
Test MSE = 0.026911776512861252
t2m = 2.7592422227882594
p
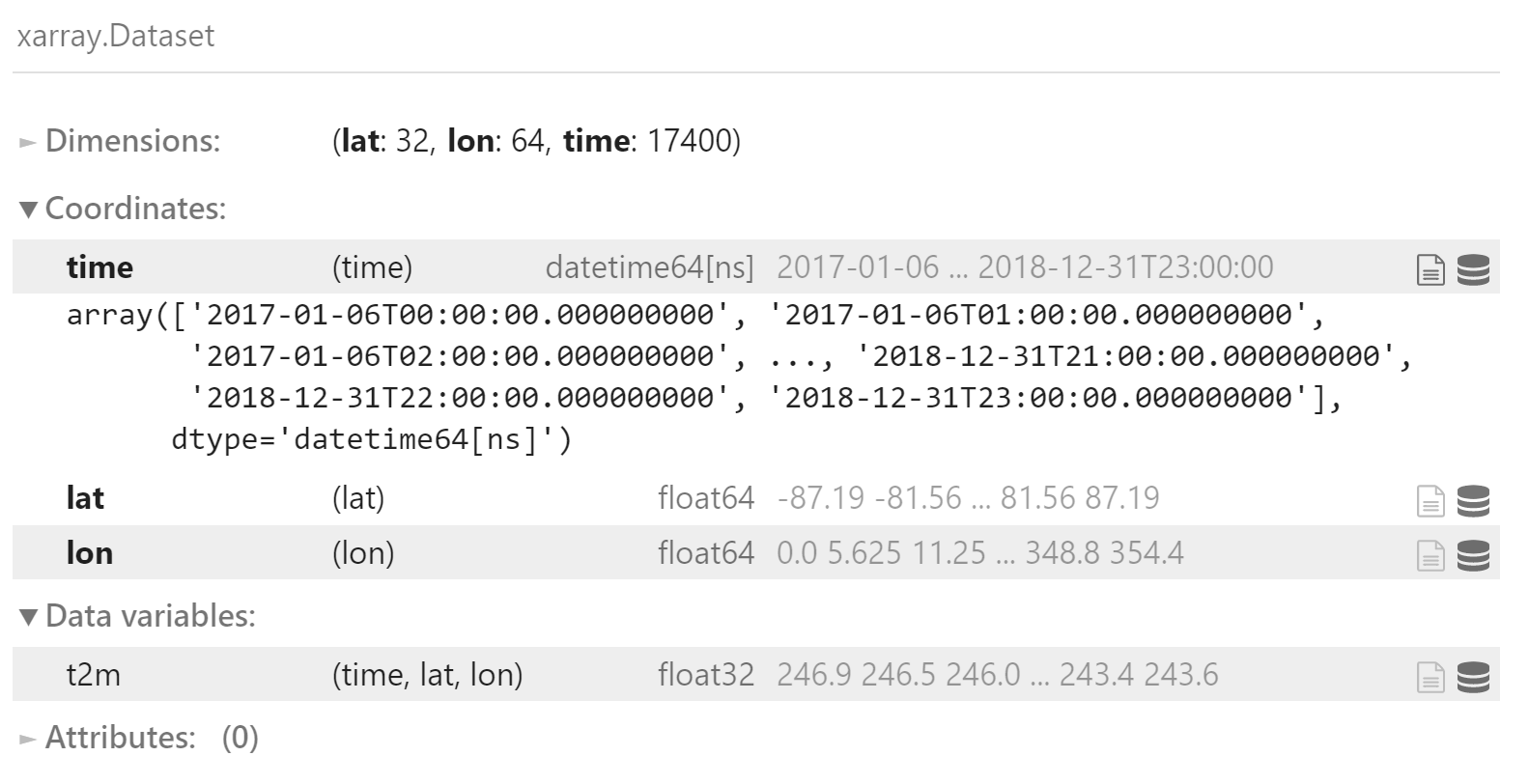
迭代预报
最后,进行迭代预测。 首先,我们训练 6 小时预报模型,然后构建长达 120 小时的迭代预报。
def create_iterative_fc(
state,
model,
lead_time_h=6,
max_lead_time_h=5*24
):
max_fc_steps = max_lead_time_h // lead_time_h
fcs_z500, fcs_t850 = [], []
for fc_step in tqdm(range(max_fc_steps)):
# 对某个预报时长 (fc_step),同时计算所有 time 维度
state = model.predict(state)
# 恢复原始值
fc_z500 = state[:, :nlat*nlon].copy() * data_std.z.values + data_mean.z.values
fc_t850 = state[:, nlat*nlon:].copy() * data_std.t.values + data_mean.t.values
fc_z500 = fc_z500.reshape((-1, nlat, nlon))
fc_t850 = fc_t850.reshape((-1, nlat, nlon))
# 保存预测结果
fcs_z500.append(fc_z500)
fcs_t850.append(fc_t850)
# 维度:预报时长,原始数据三个维度 (起报时间,纬度,经度)
return [
xr.DataArray(
np.array(fcs),
dims=['lead_time', 'time', 'lat', 'lon'],
coords={
'lead_time': np.arange(
lead_time_h,
max_lead_time_h + lead_time_h,
lead_time_h
),
'time': z500_test.time,
'lat': z500_test.lat,
'lon': z500_test.lon
}
) for fcs in [fcs_z500, fcs_t850]
]
训练 6 小时预报模型
p, m = train_lr(
6,
input_vars=['z', 't'],
output_vars=['z', 't'],
data_subsample=5
)
Train MSE = 0.003383433446288109
Test MSE = 0.004286044742912054
to_pickle(m, f'{baseline_dir}/saved_models/lr_6h_z_t_z_t.pkl')
m = read_pickle(f'{baseline_dir}/saved_models/lr_6h_z_t_z_t.pkl')
重组测试集,展开为一维数组
data_test.z.values.shape
(17520, 4096)
state = np.concatenate([
data_test.z.values.reshape(-1, nlat*nlon),
data_test.t.values.reshape(-1, nlat*nlon)
], 1)
state.shape
迭代预报
fc_z500_6h_iter, fc_t850_6h_iter = create_iterative_fc(state, m)
保存结果
fc_iter = xr.Dataset({'z': fc_z500_6h_iter, 't': fc_t850_6h_iter})
fc_iter.to_netcdf(f'{baseline_dir}/lr_6h_iter.nc')
参考
论文
WeatherBench: A Benchmark Data Set for Data‐Driven Weather Forecasting
代码
https://github.com/pangeo-data/WeatherBench
WeatherBench 系列文章
