简要介绍轴向上的聚合函数

Python 矩阵库中都会包含对数组的聚合函数（也叫作缩减函数），比如 sum，mean，std 等。

这些方法都可以直接调用，返回单一的标量值。 也可以指定某个坐标轴，沿给定轴向上进行聚合，形成一个下降一个维度的数组。

本文以 sum 方法为例，通过图示简要介绍二维和三维矩阵中沿轴向的聚合函数。

二维矩阵

使用 NumPy 构造一个 2 x 3 的二维矩阵。

import numpy as np

A = np.arange(6).reshape(2, 3)
A

array([[0, 1, 2],
       [3, 4, 5]])

生成的数组如下图所示，有两个维度。 第一个维度（dim 0）表示一行，第二个维度表示一列（dim 1）。

求和

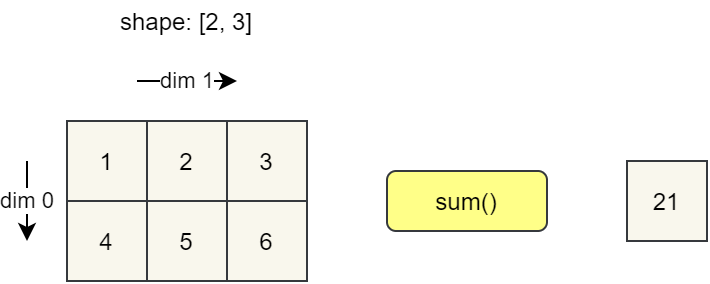
调用不带参数的 sum() 方法，返回一个标量，即数组中所有元素的和。

A.sum()

15

下图是求和的示意图，在两个维度上累加，得到最终的结果。

维度 0 求和

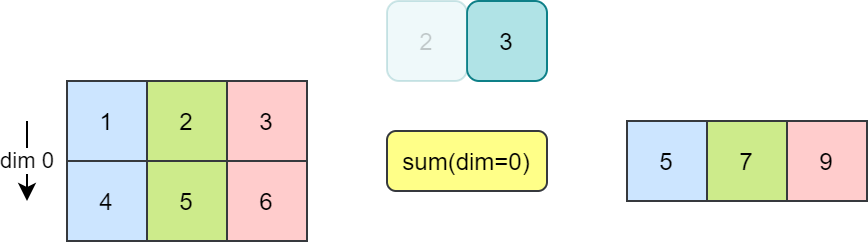
沿维度 0 求和，即沿列求和

A.sum(axis=0)

array([3, 5, 7])

沿维度 0 求和相当于合并维度 0，仅保留维度 1，即将多行合并为 1 行，仅保留 3 列数据。 求和过程如下图所示。

维度 1 求和

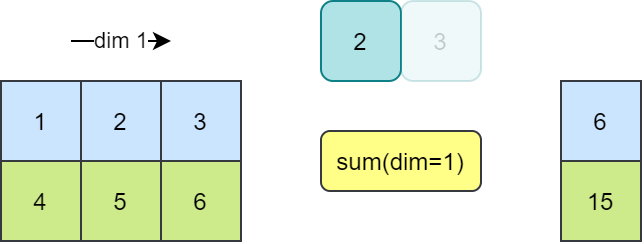
沿维度 1 求和，即沿行求和

A.sum(axis=1)

array([ 3, 12])

沿维度 1 求和相当于合并维度 1，仅保留维度 0。 即将多列合并为 1 列，仅保留 2 行数据。 求和过程如下图所示。

三维数组

使用 NumPy 构造一个 2 x 3 x 4 的三维数组

B = np.arange(24).reshape((2, 3, 4))
B

array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])

生成的数组如下图所示，有三个维度。 相当于两个 3 x 4 的二维矩阵堆叠在一起，形成第三维。

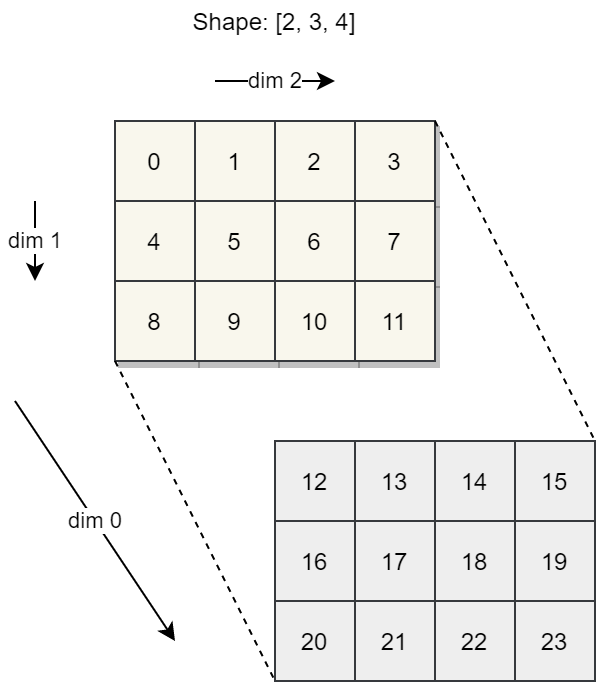
求和

B.sum()

276

维度 0 求和

沿维度 0 求和

B.sum(axis=0)

array([[12, 14, 16, 18],
       [20, 22, 24, 26],
       [28, 30, 32, 34]])

求和示意图如下所示。沿维度 0 求和后，返回 3 x 4 的矩阵。

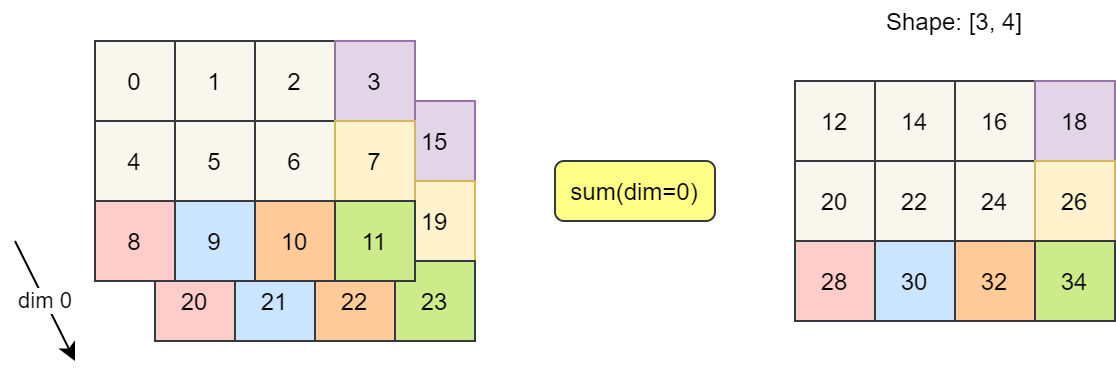
具体求和过程如下图所示。结果矩阵中的每个元素，都是两个堆叠的 3 x 4 矩阵上对应元素的和。

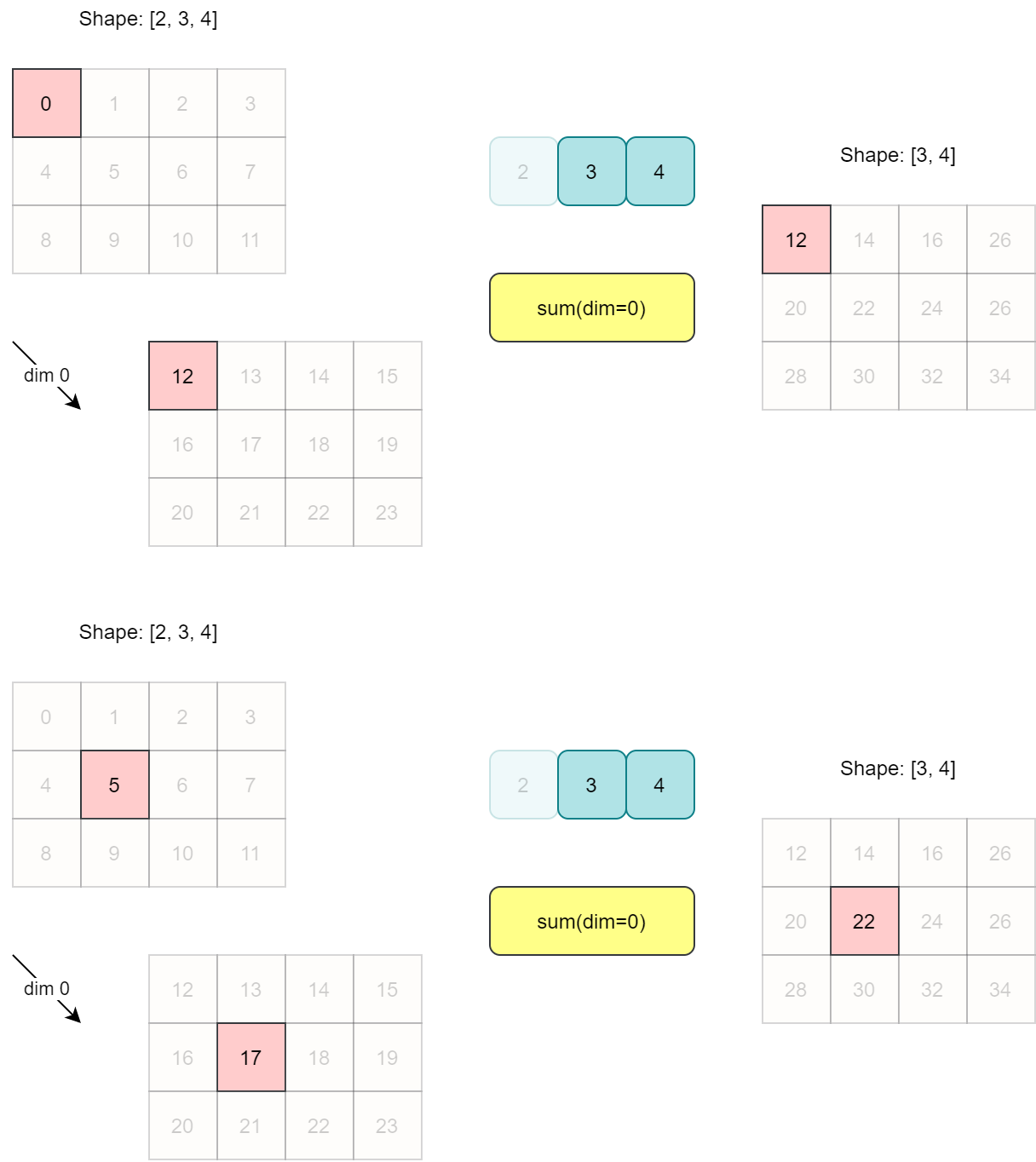
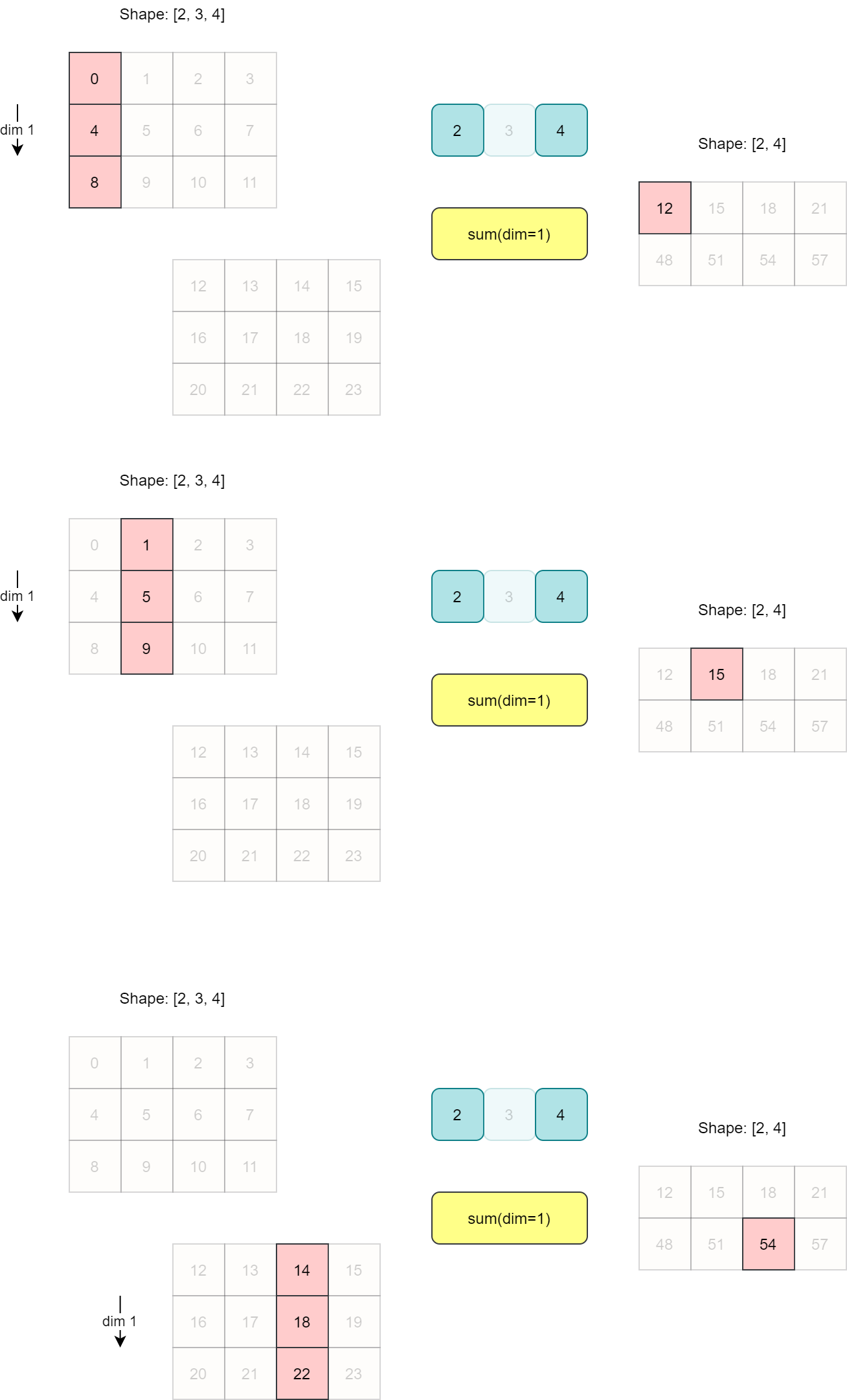
维度 1 求和

沿维度 1 求和

B.sum(axis=1)

array([[12, 15, 18, 21],
       [48, 51, 54, 57]])

求和示意图如下所示。沿维度 1 求和后，返回 2 x 4 的矩阵。

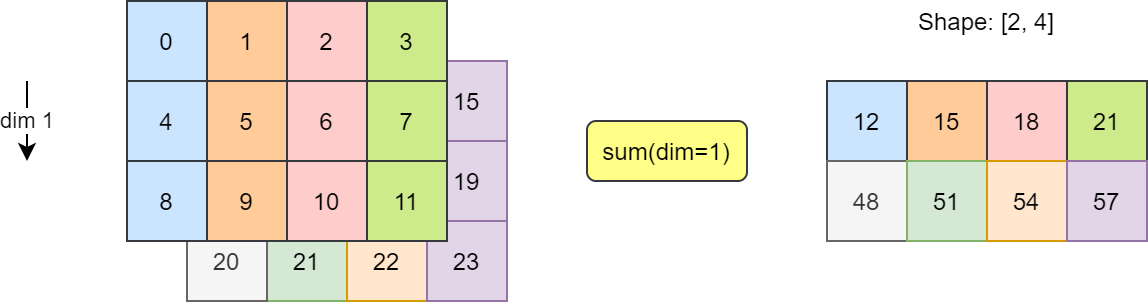
具体求和过程如下图所示。

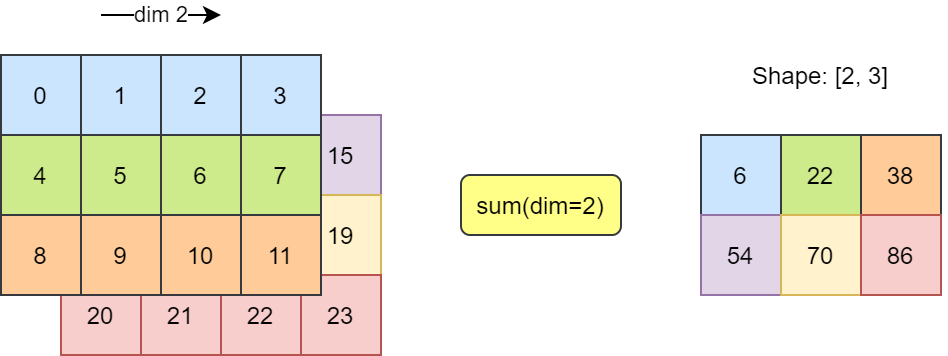
维度 2 求和

沿维度 2 求和

B.sum(axis=2)

array([[ 6, 22, 38],
       [54, 70, 86]])

求和示意图如下所示。沿维度 2 求和后，返回 2 x 3 的矩阵。

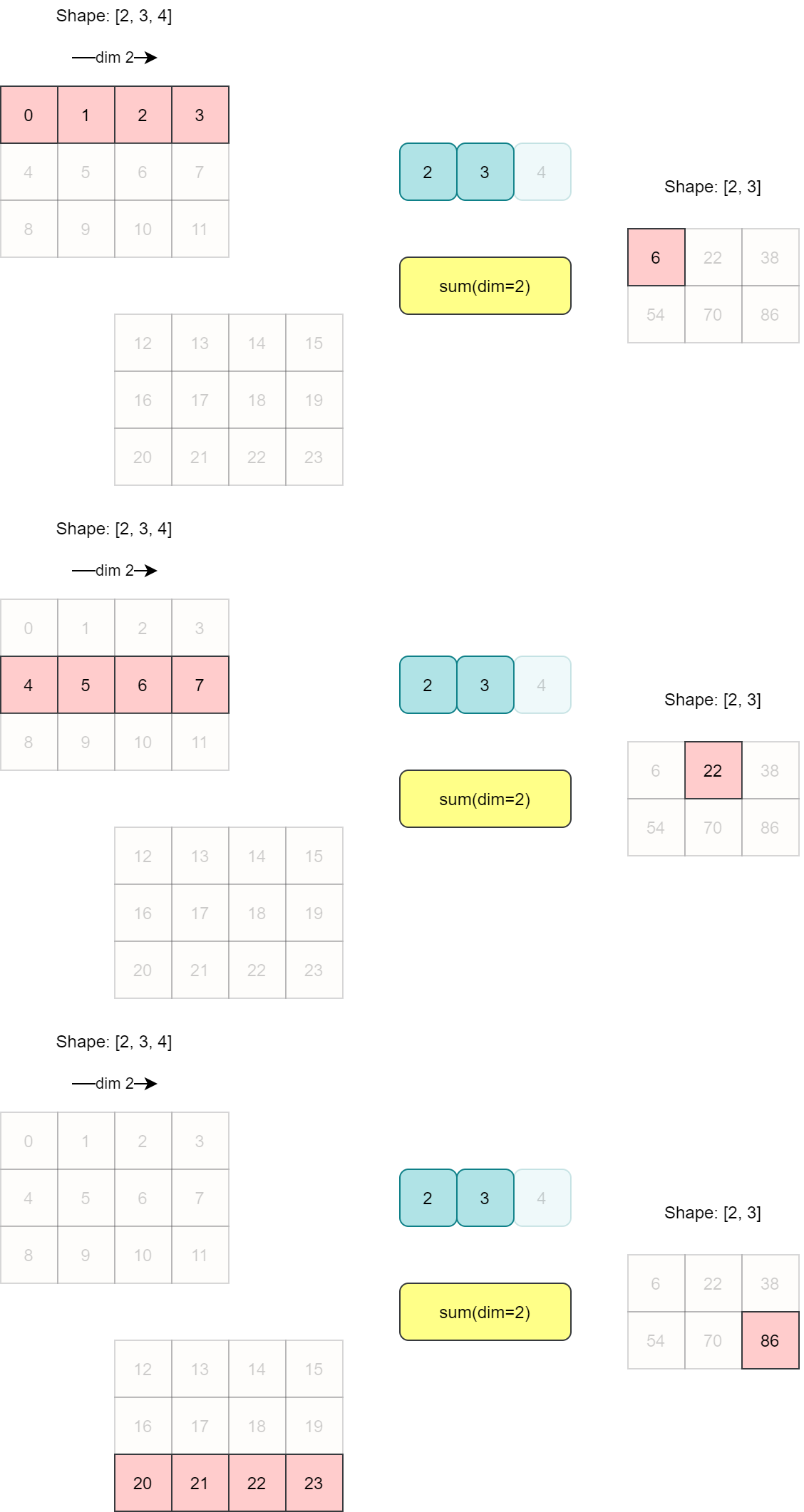
具体求和过程如下图所示。

总结

指定维度的聚合计算，就是将其余维度保持不变，将对应的该维度上的所有值就行计算并得到一个结果，再将所有这些结果组成一个新的矩阵，比原数据减少一个维度。

例如将不同的站点获取的温度值作为数组中的一行，不同的时间获取的温度作为数组中的一列。 如果想求不同时间温度的平均值，则需要合并站点，即维度 0； 如果想求每个站点的平均温度，则需要合并时间，即维度 1。

主流的 Python 矩阵库都有沿维度合并的功能，函数参数的名称可能不一样，但背后的原理都是相同的。