R语言实战:聚类
目录
本文内容来自《R 语言实战》(R in Action, 2nd),有部分修改
层次聚类:hierarchical agglomerative clustering
每个观测值自成一类,每次两两合并,直到所有类被聚成一类
常用方法:
- 单联动 single linkage
- 全联动 complete linkage
- 平均联动 average linkage
- 质心 centroid
- Ward 方法
划分聚类:patitioning clustering
指定类的个数K,随机分成K类,再重新形成聚合的类
常用方法:
- K 均值 K-means
- 围绕中心点的划分 PAM
library(flexclust)
library(rattle)
聚类分析的一般步骤
- 选择合适的变量
- 缩放数据:标准化或其他方法
- 寻找异常点:删掉异常点或者使用对异常值稳健的聚类方法
- 计算距离
- 选择聚类算法
- 获得一种或多种聚类方法
- 确定类的数目
- 获得最终的聚类解决方案
- 结果可视化
- 解读类
- 验证结果
计算距离
欧几里得距离
data(nutrient, package="flexclust")
head(nutrient, 4)
energy protein fat calcium iron
BEEF BRAISED 340 20 28 9 2.6
HAMBURGER 245 21 17 9 2.7
BEEF ROAST 420 15 39 7 2.0
BEEF STEAK 375 19 32 9 2.6
dist() 函数,默认返回下三角矩阵
d <- dist(nutrient)
as.matrix(d)[1:4, 1:4]
BEEF BRAISED HAMBURGER BEEF ROAST BEEF STEAK
BEEF BRAISED 0.00000 95.6400 80.93429 35.24202
HAMBURGER 95.64000 0.0000 176.49218 130.87784
BEEF ROAST 80.93429 176.4922 0.00000 45.76418
BEEF STEAK 35.24202 130.8778 45.76418 0.00000
层次聚类分析
算法:
- 定义每个观测值(行或单元)为一类;
- 计算每类和其他各类的距离;
- 把距离最短的两类合并成一类;
- 重复上两步,直到包含所有观测值的类个合并成单个的类为止
聚类方法:
- 单联动:一个类中的点与另一个类中的点的最小距离
- 全联动:一个类中的点与另一个类中的点的最大距离
- 平均联动::一个类中的点与另一个类中的点的平均距离
- 质心:两类中质心(变量均值向量)之间的距离
- Ward 法:两个类之间所有变量的方差分析的平方和
营养数据的平均联动聚类,使用层次聚类函数 hlclust() 实现
row.names(nutrient) <- tolower(row.names(nutrient))
nutrient.scaled <- scale(nutrient)
d <- dist(nutrient.scaled)
fit.average <- hclust(d, method="average")
plot(
fit.average,
hang=-1,
cex=.8,
main="Vaerage Linkage Clustering"
)
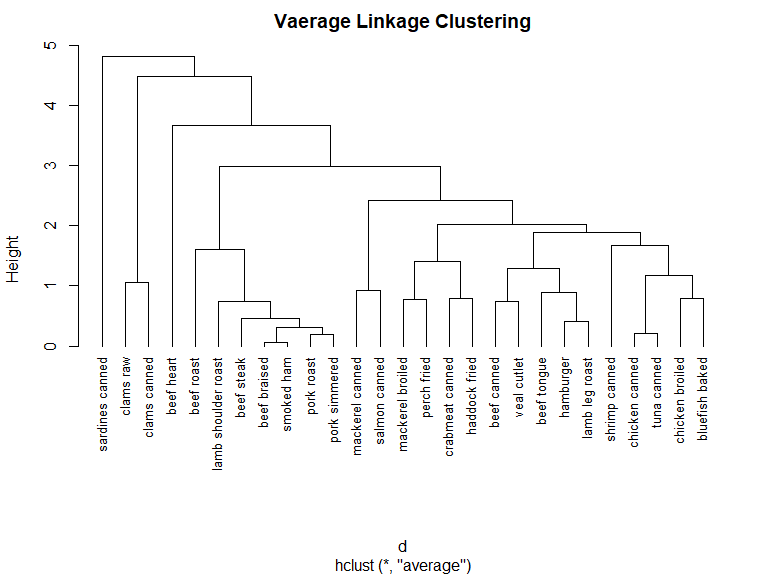
使用 NbClust 包辅助确定聚类的最佳数目
library(NbClust)
NbClust() 函数输出平均联动聚类的最佳聚类最佳数目
nc <- NbClust(
nutrient.scaled,
distance="euclidean",
min.nc=2,
max.nc=15,
method="average"
)
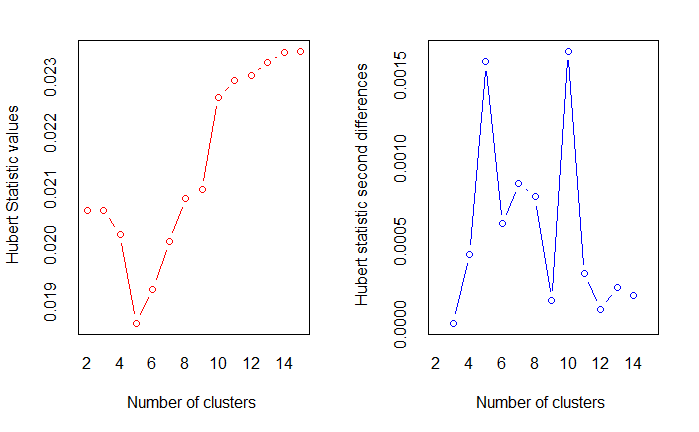
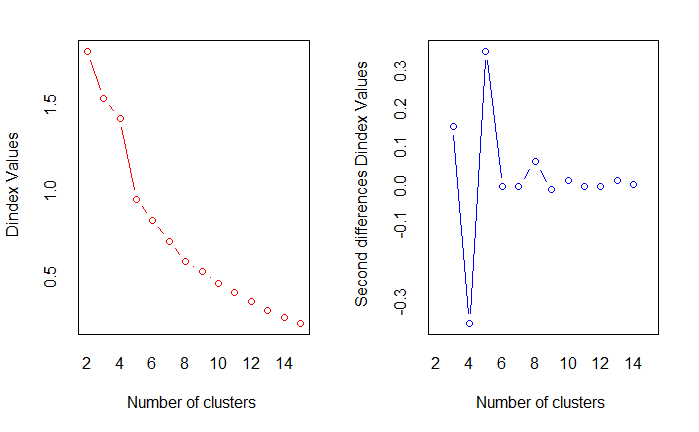
table(nc$Best.nc[1,])
0 1 2 3 4 5 9 10 13 14 15
2 1 4 4 2 4 1 1 2 1 4
barplot(
table(nc$Best.nc[1,]),
xlab="Number of Clusters",
ylab="Number of Criteria",
main="Number of Clusters Chosed by 26 Criteria"
)
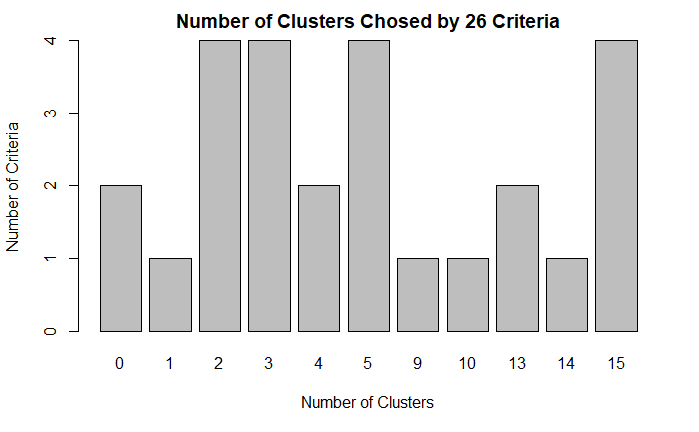
聚类为 5 类
clusters <- cutree(fit.average, k=5)
table(clusters)
clusters
1 2 3 4 5
7 16 1 2 1
使用原始数据描述聚类
aggregate(
nutrient,
by=list(cluster=clusters),
median
)
cluster energy protein fat calcium iron
1 1 340.0 19 29 9 2.50
2 2 170.0 20 8 13 1.45
3 3 160.0 26 5 14 5.90
4 4 57.5 9 1 78 5.70
5 5 180.0 22 9 367 2.50
使用标准度量描述聚类
aggregate(
as.data.frame(nutrient.scaled),
by=list(cluster=clusters),
median
)
cluster energy protein fat calcium iron
1 1 1.3101024 0.0000000 1.3785620 -0.4480464 0.08110456
2 2 -0.3696099 0.2352002 -0.4869384 -0.3967868 -0.63743114
3 3 -0.4684165 1.6464016 -0.7534384 -0.3839719 2.40779157
4 4 -1.4811842 -2.3520023 -1.1087718 0.4361807 2.27092763
5 5 -0.2708033 0.7056007 -0.3981050 4.1396825 0.08110456
绘制层次关系图,使用 rect.hclust() 函数标出分类
plot(
fit.average,
hang=-1,
cex=.8,
main="Average Linkage Cluster\n5 Cluster Solution"
)
rect.hclust(fit.average, k=5)
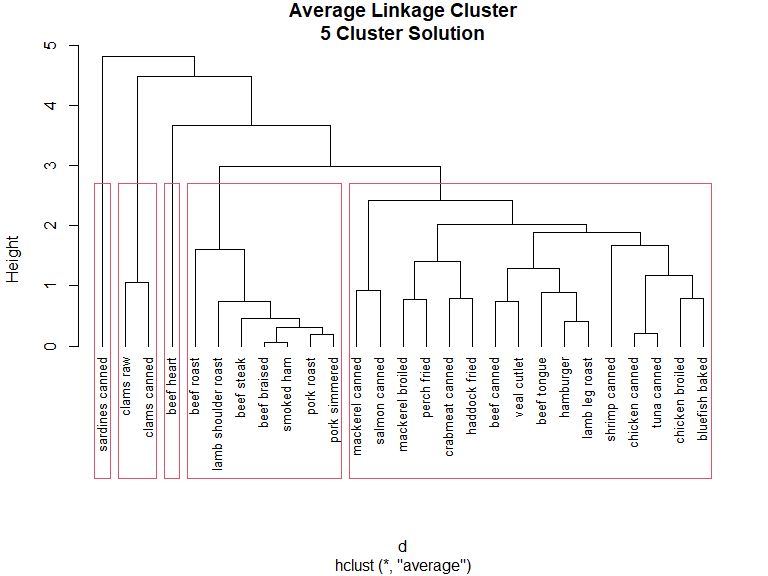
层次聚类难以应用到大样本中。
划分聚类分析
K均值聚类
算法:
- 选择 K 个中心;
- 将每个数据点分配到离它最近的中心点;
- 重新计算每类中的点到该类中心点距离的平均值
- 分配每个数据到它最近的中心点
- 重复步骤 3 和步骤 4,直到所有的观测值不再被分配或是达到最大的迭代次数
data(wine, package="rattle")
head(wine)
Type Alcohol Malic Ash Alcalinity Magnesium Phenols Flavanoids
1 1 14.23 1.71 2.43 15.6 127 2.80 3.06
2 1 13.20 1.78 2.14 11.2 100 2.65 2.76
3 1 13.16 2.36 2.67 18.6 101 2.80 3.24
4 1 14.37 1.95 2.50 16.8 113 3.85 3.49
5 1 13.24 2.59 2.87 21.0 118 2.80 2.69
6 1 14.20 1.76 2.45 15.2 112 3.27 3.39
Nonflavanoids Proanthocyanins Color Hue Dilution Proline
1 0.28 2.29 5.64 1.04 3.92 1065
2 0.26 1.28 4.38 1.05 3.40 1050
3 0.30 2.81 5.68 1.03 3.17 1185
4 0.24 2.18 7.80 0.86 3.45 1480
5 0.39 1.82 4.32 1.04 2.93 735
6 0.34 1.97 6.75 1.05 2.85 1450
绘制不同分类数类中总的平方值对聚类数量的曲线
wssplot <- function(data, nc=15, seed=1234){
wss <- (nrow(data)-1)*sum(apply(data, 2, var))
for(i in 2:nc) {
set.seed(seed)
wss[i] <- sum(kmeans(data, centers=i)$withinss)
}
plot(
1:nc,
wss,
type="b",
xlab="Number of Clusters",
ylab="Within groups sum of squares"
)
}
决定聚类个数
df <- scale(wine[-1])
wssplot(df)
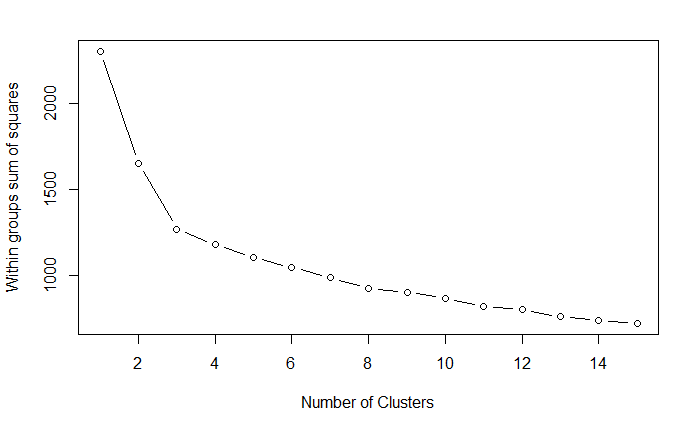
set.seed(1234)
nc <- NbClust(
df,
min.nc=2,
max.nc=15,
method="kmeans"
)
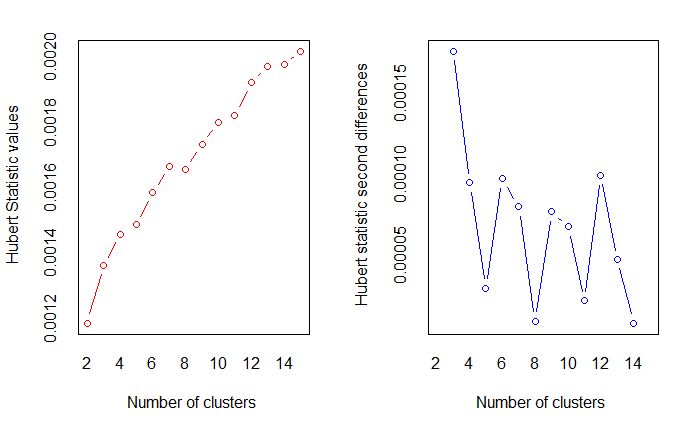
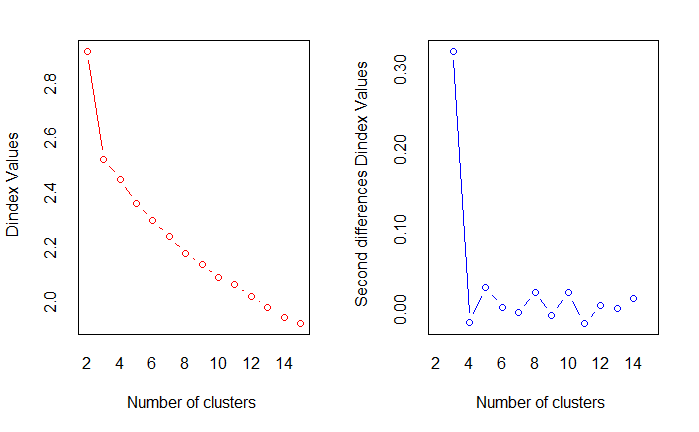
table(nc$Best.nc[1,])
0 1 2 3 14 15
2 1 2 19 1 1
barplot(
table(nc$Best.nc[1,]),
xlab="Number of Clusters",
ylab="Number of Criteria",
main="Number of Clusters Chosed by 26 Criteria"
)
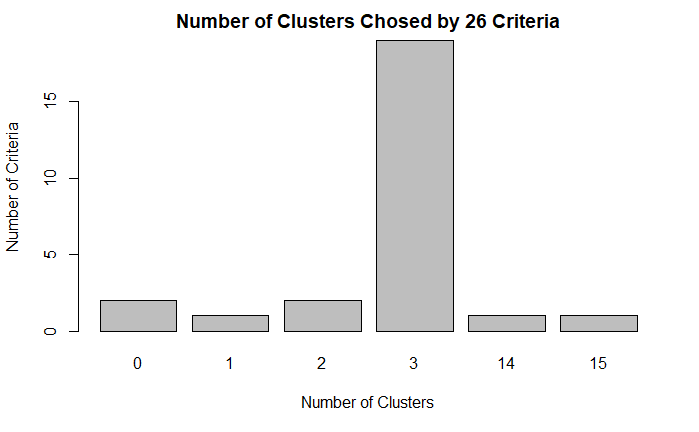
使用 3 类进行 K 均值聚类分析
set.seed(1234)
fit.km <- kmeans(df, 3, nstart=25)
fit.km$size
[1] 62 65 51
fit.km$centers
Alcohol Malic Ash Alcalinity Magnesium Phenols
1 0.8328826 -0.3029551 0.3636801 -0.6084749 0.57596208 0.88274724
2 -0.9234669 -0.3929331 -0.4931257 0.1701220 -0.49032869 -0.07576891
3 0.1644436 0.8690954 0.1863726 0.5228924 -0.07526047 -0.97657548
Flavanoids Nonflavanoids Proanthocyanins Color Hue
1 0.97506900 -0.56050853 0.57865427 0.1705823 0.4726504
2 0.02075402 -0.03343924 0.05810161 -0.8993770 0.4605046
3 -1.21182921 0.72402116 -0.77751312 0.9388902 -1.1615122
Dilution Proline
1 0.7770551 1.1220202
2 0.2700025 -0.7517257
3 -1.2887761 -0.4059428
计算每类的统计值
aggregate(
wine[-1],
by=list(cluster=fit.km$cluster),
mean
)
cluster Alcohol Malic Ash Alcalinity Magnesium Phenols
1 1 13.67677 1.997903 2.466290 17.46290 107.96774 2.847581
2 2 12.25092 1.897385 2.231231 20.06308 92.73846 2.247692
3 3 13.13412 3.307255 2.417647 21.24118 98.66667 1.683922
Flavanoids Nonflavanoids Proanthocyanins Color Hue Dilution
1 3.0032258 0.2920968 1.922097 5.453548 1.0654839 3.163387
2 2.0500000 0.3576923 1.624154 2.973077 1.0627077 2.803385
3 0.8188235 0.4519608 1.145882 7.234706 0.6919608 1.696667
Proline
1 1100.2258
2 510.1692
3 619.0588
K 均值是否揭示类型变量中真正的数据结构
ct.km <- table(wine$Type, fit.km$cluster)
ct.km
1 2 3
1 59 0 0
2 3 65 3
3 0 0 48
使用 flexclust 包计算兰德指数 (Rank index),量化类型变量和类之间的协议
randIndex(ct.km)
ARI
0.897495
围绕中心点的划分
- 随机选择 K 个观测值,每个都称为中心点
- 计算观测值到各个中心的距离/相异性
- 把每个观测值分配到最近的中心点
- 计算每个中心点到每个观测值的距离的总和 (总成本)
- 选择一个该类中不是中心的点,并和中心点互换
- 重新把每个点分配到距它最近的中心点
- 再次计算总成本
- 如果总成本比步骤 4 计算的总成本少,把新的点作为中心点;
- 重复步骤 5 ~ 8 直到中心点不再改变
library(cluster)
使用 pam() 进行 PAM 聚类
set.seed(1234)
fit_pam <- pam(
wine[-1],
k=3,
stand=TRUE
)
中心点
fit_pam$medoids
Alcohol Malic Ash Alcalinity Magnesium Phenols Flavanoids
[1,] 13.48 1.81 2.41 20.5 100 2.70 2.98
[2,] 12.25 1.73 2.12 19.0 80 1.65 2.03
[3,] 13.40 3.91 2.48 23.0 102 1.80 0.75
Nonflavanoids Proanthocyanins Color Hue Dilution Proline
[1,] 0.26 1.86 5.1 1.04 3.47 920
[2,] 0.37 1.63 3.4 1.00 3.17 510
[3,] 0.43 1.41 7.3 0.70 1.56 750
绘图
clusplot(
fit_pam,
main="Bivariate Cluster Plot"
)
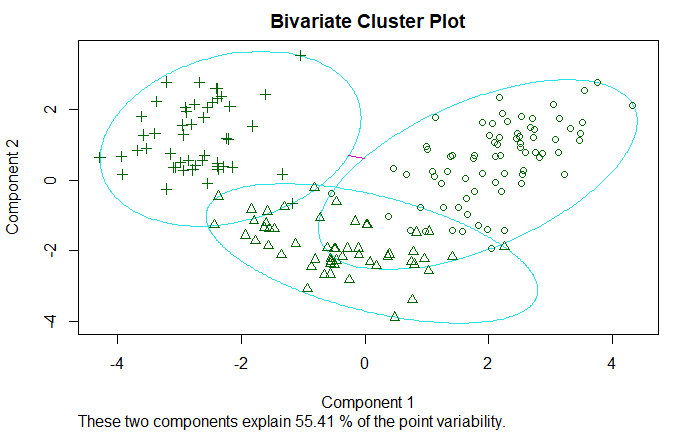
效果验证,不如 K 均值聚类
ct_pam <- table(wine$Type, fit_pam$clustering)
ct_pam
1 2 3
1 59 0 0
2 16 53 2
3 0 1 47
randIndex(ct_pam)
ARI
0.6994957
避免不存在的类
library(fMultivar)
生成 1000 个相关系数为 0.5 的二元正态分布
set.seed(1234)
df <- rnorm2d(1000, rho=.5)
df <- as.data.frame(df)
plot(
df,
main="Bivirate Normal Distribution with rho=0.5"
)
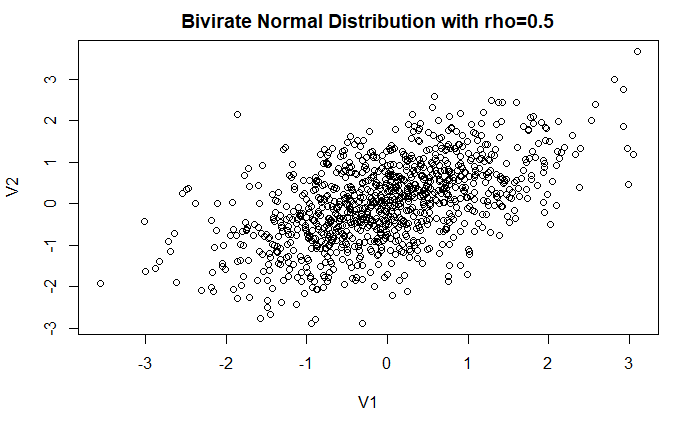
使用前面的方法确定聚类个数
wssplot(df)
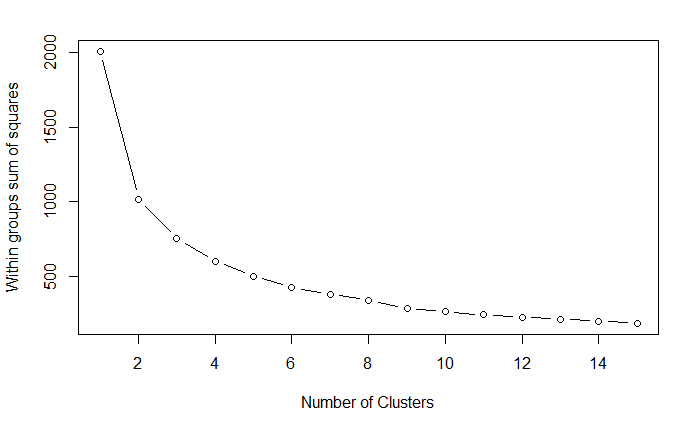
nc <- NbClust(
df,
min.nc=2,
max.nc=15,
method="kmeans"
)
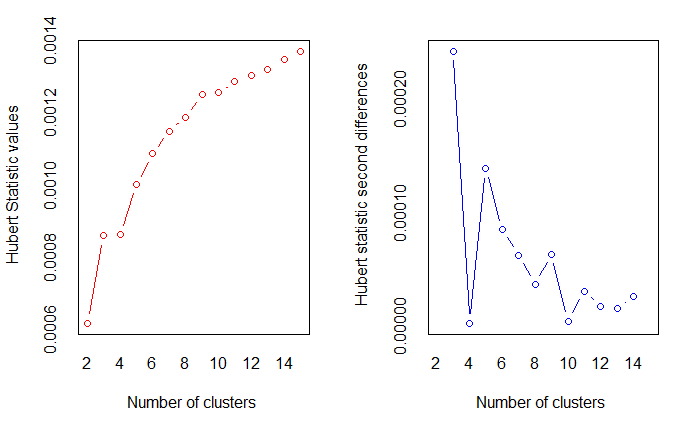
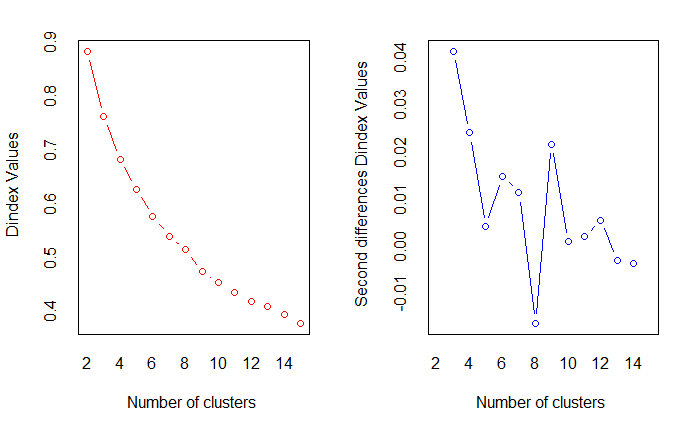
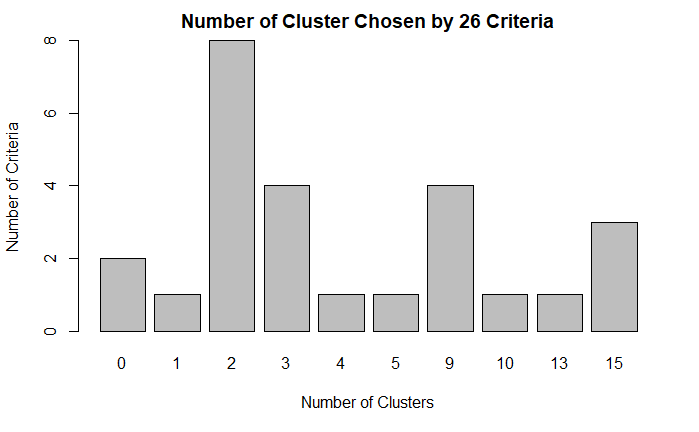
barplot(
table(nc$Best.n[1,]),
xlab="Number of Clusters",
ylab="Number of Criteria",
main="Number of Cluster Chosen by 26 Criteria"
)
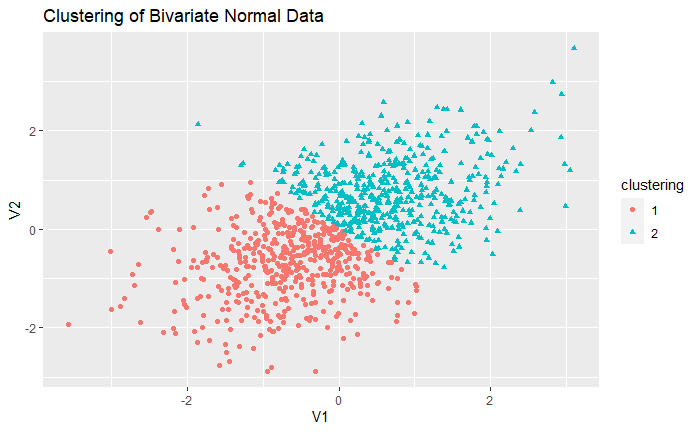
使用 PAM 进行双聚类分析
library(ggplot2)
fit <- pam(df, k=2)
df$clustering <- factor(fit$clustering)
ggplot(
data=df,
aes(x=V1, y=V2, color=clustering, shape=clustering)
) +
geom_point() +
ggtitle("Clustering of Bivariate Normal Data")
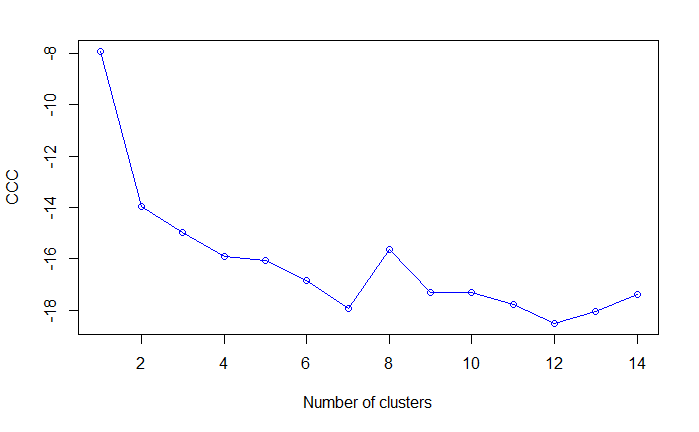
使用 NbClust 包中的立方聚类规则 (Cubic Cluster Criteria, CCC)。 当 CCC 的值为负且对于两类或是更多的类递减是,就是典型的单峰分布。
plot(
nc$All.index[,4],
type="o",
ylab="CCC",
xlab="Number of clusters",
col="blue"
)
参考
https://github.com/perillaroc/r-in-action-study
R 语言实战
