R语言实战：时间序列

March 30, 2021 (最后修改: April 02, 2021)

programming/R

本文内容来自《R 语言实战》(R in Action, 2nd)，有部分修改

横截面数据 (cross-sectional)：给定一个时间点测量变量的值

纵向数据 (longitudinal)：随着时间的变化反复测量变量值

时间序列：给定一段时间内有规律地记录的观测值

在 R 中生成时序对象

时间序列对象 (time-series object)：R 中一种包括观测值、起始时间、终止时间以及周期 (如月、季度或年) 的结构

ts() 生成时间序列对象

frequency 参数指定每个单位时间所包含的观测值数量

frequency=1：年数据
frequency=4：季度数据
frequency=12：月数据

sales <- c(
  18, 33, 41, 7, 34, 35, 
  24, 25, 24, 21, 25, 20,
  22, 31, 40, 29, 25, 21,
  22, 54, 32, 25, 26, 35
)
tsales <- ts(
  sales,
  start=c(2003, 1),
  frequency=12
)
tsales

     Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
2003  18  33  41   7  34  35  24  25  24  21  25  20
2004  22  31  40  29  25  21  22  54  32  25  26  35

plot(tsales)

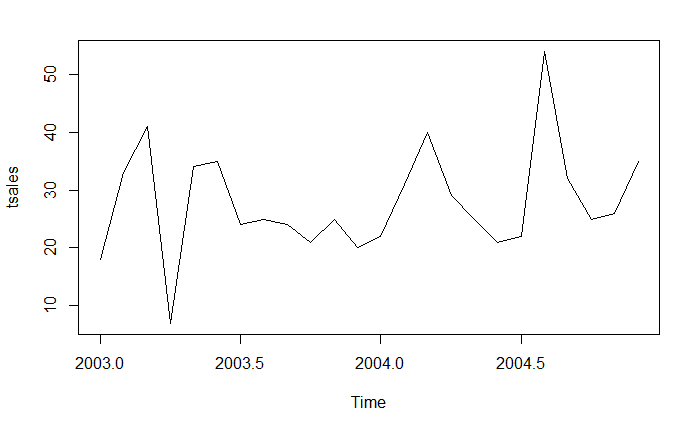
查看时序数据属性：

起始时间

start(tsales)

[1] 2003    1

终止时间

end(tsales)

[1] 2004   12

频率

frequency(tsales)

[1] 12

window() 函数生成子时序

tsales.subset <- window(
  tsales,
  start=c(2003, 5),
  end=c(2004, 6)
)
tsales.subset

     Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
2003                  34  35  24  25  24  21  25  20
2004  22  31  40  29  25  21

时序的平滑化和季节性分解

通过简单移动平均进行平滑处理

处理时序数据的第一步是画图

居中移动平均 (centered moving average)

$$ S_t = (Y_{t-q} + … + Y_t + … + Y_{t+q})/(2q + 1) $$

代价：损失最后 (k-1)/2 个观测值

library(forecast)

opar <- par(no.readonly=TRUE)
par(mfrow=c(2, 2))
ylim <- c(min(Nile), max(Nile))

plot(
  Nile,
  main="Raw time series"
)
plot(
  ma(Nile, 3),
  main="Simple Moving Averages (k=3)",
  ylim=ylim
)
plot(
  ma(Nile, 7),
  main="Simple Moving Averages (k=7)",
  ylim=ylim
)
plot(
  ma(Nile, 15),
  main="Simple Moving Averages (k=15)",
  ylim=ylim
)
par(opar)

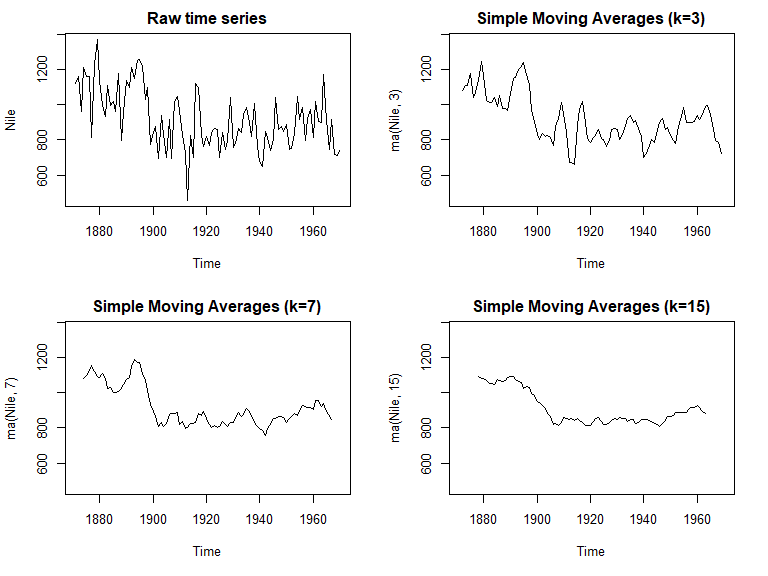
季节性分解

趋势因子 (trend component)：捕捉长期变化

季节性因子 (seasonal component)：捕捉一年内的周期性变化

随机 (误差) 因子 (irregular/error component)：捕捉不能被趋势和季节效应解释的变化

相加模型：

$$ Y_t = Trend_t + Seasonal_t + Irregular_t $$

相乘模型：

$$ Y_t = Trend_t \times Seasonal_t \times Irregular_t $$

相乘模型可以通过对数变化转成相加模型

AirPassengers 序列

plot(AirPassengers)

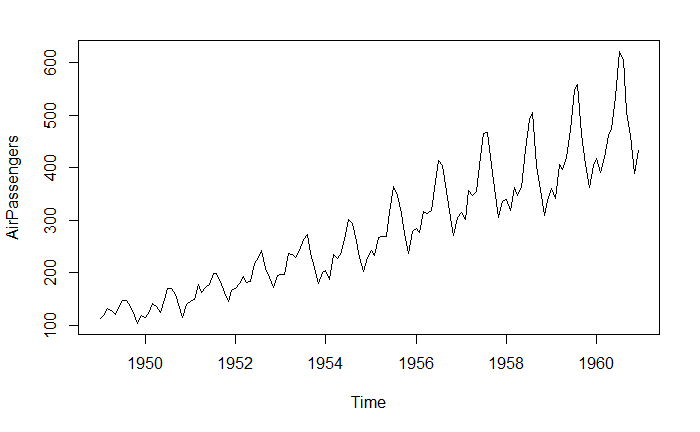
lAirPassengers <- log(AirPassengers)
plot(
  lAirPassengers,
  ylab="log(AirPassengers)"
)

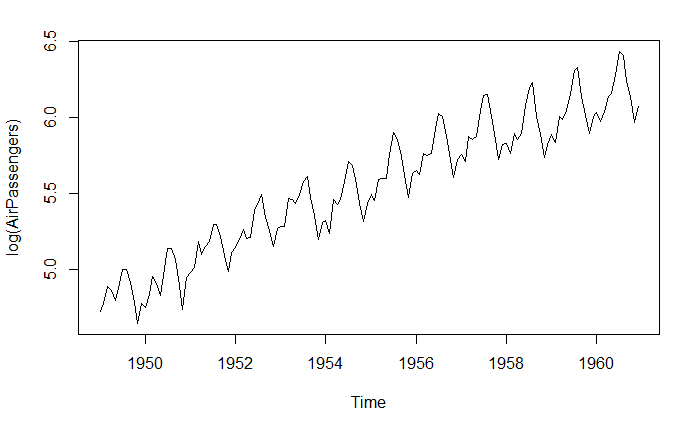
stl() 函数分解序列为趋势项、季节项和随机项

fit <- stl(
  lAirPassengers,
  s.window="period"
)
plot(fit)

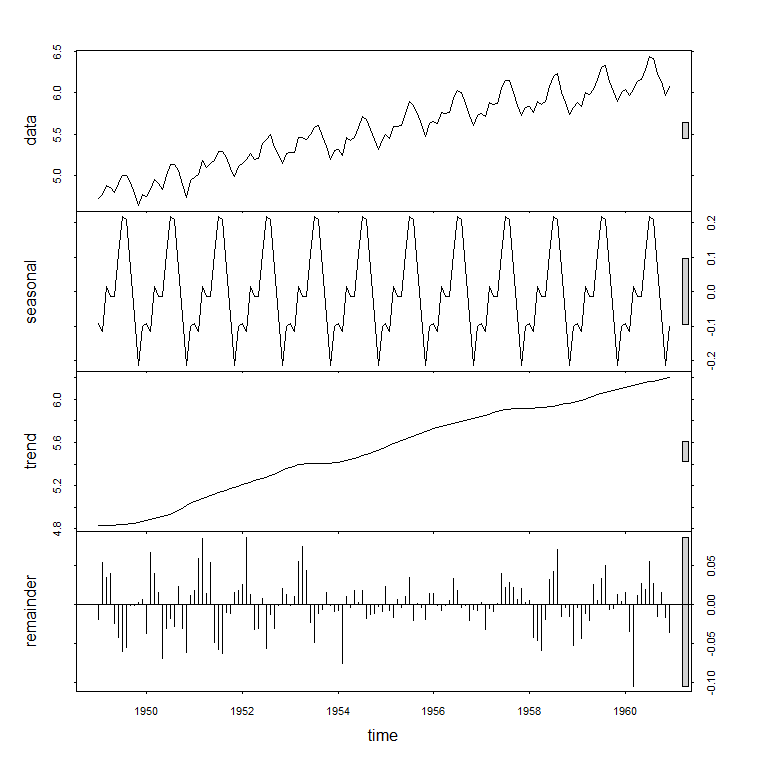
上图中右侧的灰条代表一样的量级

fit$time.series

            seasonal    trend     remainder
Jan 1949 -0.09164042 4.829389 -0.0192493585
Feb 1949 -0.11402828 4.830368  0.0543447685
Mar 1949  0.01586585 4.831348  0.0355884457
...
Oct 1960 -0.07024836 6.187594  0.0160525773
Nov 1960 -0.21352774 6.196307 -0.0166330133
Dec 1960 -0.10063625 6.204752 -0.0356905175

exp(fit$time.series)

          seasonal    trend remainder
Jan 1949 0.9124332 125.1344 0.9809347
Feb 1949 0.8922327 125.2571 1.0558486
Mar 1949 1.0159924 125.3798 1.0362293
...
Oct 1960 0.9321623 486.6737 1.0161821
Nov 1960 0.8077298 490.9329 0.9835046
Dec 1960 0.9042619 495.0963 0.9649389

绘图

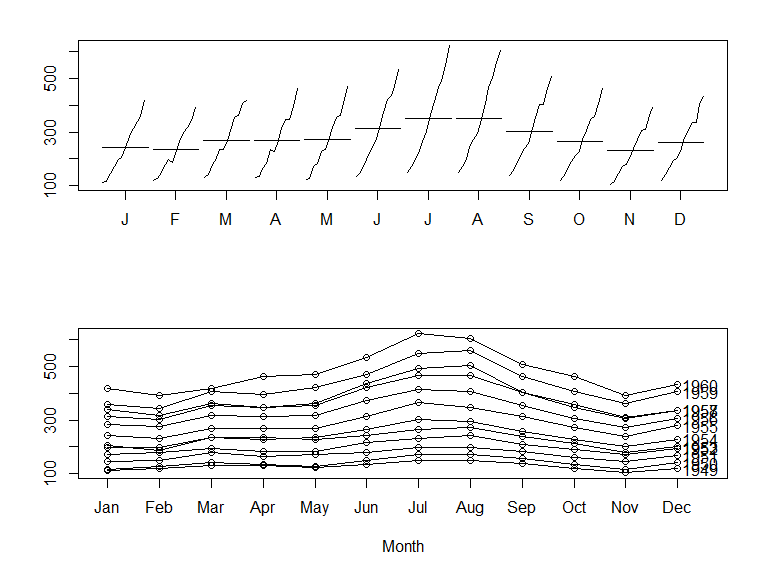
使用 R 自带的 monthplot() 函数和 forecast 包中的 seasonplot() 函数

par(mfrow=c(2, 1))
monthplot(
  AirPassengers,
  xlab="",
  ylab=""
)
seasonplot(
  AirPassengers,
  year.labels="TRUE",
  main=""
)

指数预测模型

单指数模型 (simple/single exponential model)：水平项

双指数模型 (double exponential model) 或 Holt 指数平滑 (Holt exponential smoothing)：水平项 + 趋势项

三指数模型 (triple exponential model) 或 Holt-Winters 指数平滑 (Holt-Winters exponential smoothing)：水平项 + 趋势项 + 季节项

forecast 包的 ets() 函数的 model 参数

A 相加模型
M 相乘模型
N 无
Z 自动选择

单指数平滑

$$ Y_t = \mathit{level} + \mathit{irregular}_t $$

一步向前预测 1-step ahead forecast

$$ Y_{t+1} = c_0Y_t + c_1Y_{t-1} + c_2Y_{t-2} + c_2Y_{t_2} + \cdots $$

其中

$$ c_i = \alpha(1-\alpha)^2 \ i=0,1,2,\cdots \ 0 \leqslant \alpha \leqslant 1 $$

nhtemp 时序

plot(
  nhtemp,
  main="New Haven Annual Mean Temperature",
  xlab="Year",
  ylab=expression(paste("Temperature (", degree*F, ")",)),
)

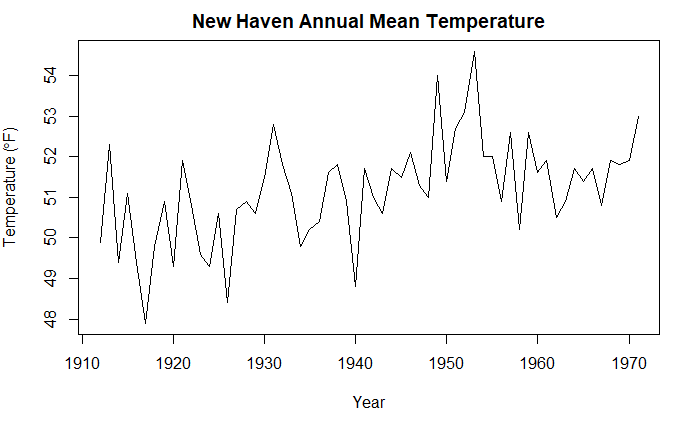
ets() 函数 model 参数由三个字母构成，分别代表：

误差项
趋势项
季节项

model="ANN" 单指数平滑

fit <- ets(nhtemp, model="ANN")
fit

ETS(A,N,N) 

Call:
 ets(y = nhtemp, model = "ANN") 

  Smoothing parameters:
    alpha = 0.1819 

  Initial states:
    l = 50.2762 

  sigma:  1.1455

     AIC     AICc      BIC 
265.9298 266.3584 272.2129

一步向前预测

forecast(fit, 1)

     Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
1972       51.87031 50.40226 53.33835 49.62512 54.11549

绘制预测值，80%/95% 置信区间

plot(
  forecast(fit, 1),
  main="New Haven Annual Mean Temperature",
  xlab="Year",
  ylab=expression(paste("Temperature (", degree*F, ")",)),
)

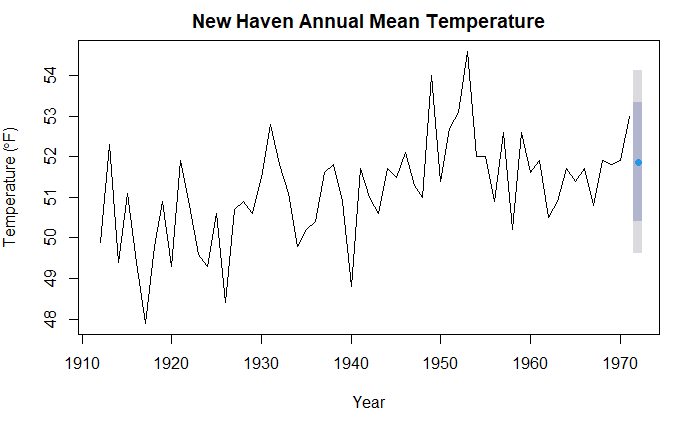
计算预测准确性

accuracy(fit)

                    ME     RMSE       MAE       MPE   MAPE      MASE
Training set 0.1460657 1.126268 0.8951225 0.2419373 1.7489 0.7512408
                     ACF1
Training set -0.006441923

度量：

ME：平均误差
RMSE：平均残差平方和的平方根
MAE：平均绝对误差
MPE：平均百分比误差
MAPE：平均绝对百分误差
MASE：平均绝对标准化误差

Holt 指数平滑和 Holt-Winters 指数平滑

alpha：水平项

beta：趋势项

gamma：季节项

Holt-Winters 指数平滑

fit <- ets(
  log(AirPassengers),
  model="AAA"
)
fit

ETS(A,A,A) 

Call:
 ets(y = log(AirPassengers), model = "AAA") 

  Smoothing parameters:
    alpha = 0.6975 
    beta  = 0.0031 
    gamma = 1e-04 

  Initial states:
    l = 4.7925 
    b = 0.0111 
    s = -0.1045 -0.2206 -0.0787 0.0562 0.2049 0.2149
           0.1146 -0.0081 -0.0059 0.0225 -0.1113 -0.0841

  sigma:  0.0383

      AIC      AICc       BIC 
-207.1694 -202.3123 -156.6826

预测未来值

pred <- forecast(fit, 5)
pred

         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
Jan 1961       6.109335 6.060306 6.158365 6.034351 6.184319
Feb 1961       6.092542 6.032679 6.152405 6.000989 6.184094
Mar 1961       6.236626 6.167535 6.305718 6.130960 6.342292
Apr 1961       6.218531 6.141239 6.295823 6.100323 6.336738
May 1961       6.226734 6.141971 6.311498 6.097100 6.356369

plot(
  pred,
  main="Forecast for Air Travel",
  ylab="Log(AirPassengers",
  xlab="Time"
)

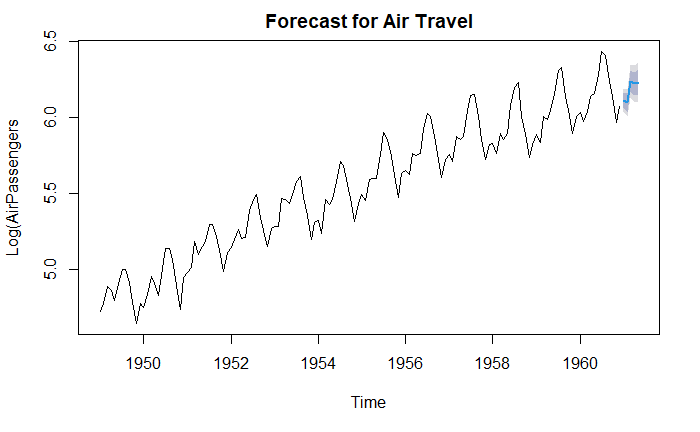
使用原始尺度预测

pred$mean <- exp(pred$mean)
pred$lower <- exp(pred$lower)
pred$upper <- exp(pred$upper)
p <- cbind(pred$mean, pred$lower, pred$upper)
dimnames(p)[[2]] <- c(
  "mean",
  "Lo 80",
  "Lo 95",
  "Hi 80",
  "Hi 95"
)
p

             mean    Lo 80    Lo 95    Hi 80    Hi 95
Jan 1961 450.0395 428.5065 417.5279 472.6544 485.0826
Feb 1961 442.5448 416.8301 403.8280 469.8459 484.9735
Mar 1961 511.1312 477.0088 459.8775 547.6945 568.0971
Apr 1961 501.9652 464.6289 446.0019 542.3017 564.9506
May 1961 506.1001 464.9691 444.5667 550.8694 576.1504

`ets()` 函数和自动预测

fit <- ets(JohnsonJohnson)
fit

ETS(M,A,A) 

Call:
 ets(y = JohnsonJohnson) 

  Smoothing parameters:
    alpha = 0.2776 
    beta  = 0.0636 
    gamma = 0.5867 

  Initial states:
    l = 0.6276 
    b = 0.0165 
    s = -0.2293 0.1913 -0.0074 0.0454

  sigma:  0.0921

     AIC     AICc      BIC 
163.6392 166.0716 185.5165

plot(
  forecast(fit),
  main="Johnson & Johnson Forecasts",
  ylab="Quarterly Earnings (Dollars)",
  xlab="Time",
  flty=2
)

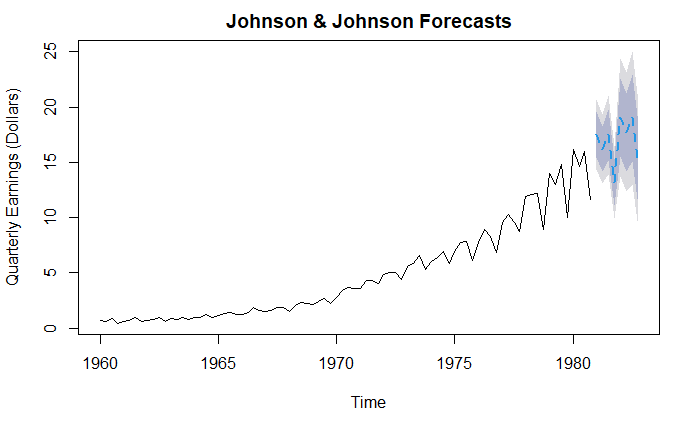
ARIMA 预测模型

概念介绍

滞后阶数 (lag)：向后追溯的观测值的数量

自相关 (Autocorrelation)：度量时序中各个观测值之间的相关性

自相关函数图 (AutoCorrelation Function plot, ACF 图)

偏相关性 (partial autocorrelation)：当序列 Y_t 和 Y_{t-k} 之间的所有值 (Y_{t-1}，Y_{t-2}，…，Y_{t-k+1}) 带来的响应都被移除后，两个序列间的相关性

PACF 图

平稳性 (stationarity)：序列的统计性质不会随着时间的推移而改变

差分 (differencing)：将时序中的每个观测值 Y_t 都替换为 Y_{t-1} - Y_{t}

ADF (Augmented Dickey-Fuller) 统计检验验证平稳性假定。

ARMA 模型含有：

自回归 (AutoRegressive, AR) 项
移动平均 (Moving Averages, MA) 项

ARIMA 模型再加上差分

ARMA 和 ARIMA 模型

验证序列的平稳性

plot(Nile)

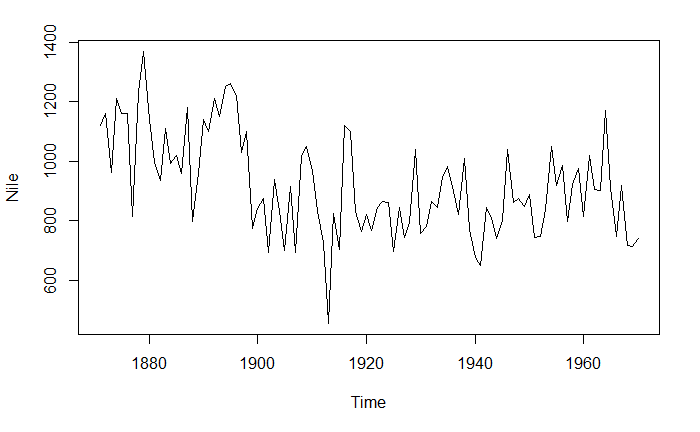
计算需要的差分次数

ndiffs(Nile)

[1] 1

差分一次

dNile <- diff(Nile)
plot(dNile)

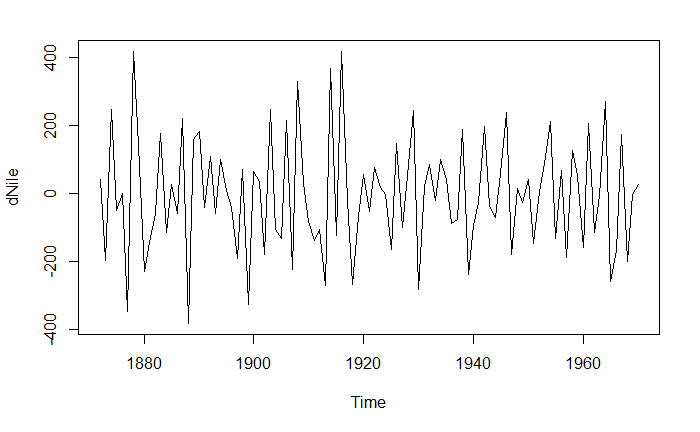
tseries 库的 adf.test() 函数评估序列的稳定性

library(tseries)

adf.test(dNile)

	Augmented Dickey-Fuller Test

data:  dNile
Dickey-Fuller = -6.5924, Lag order = 4, p-value = 0.01
alternative hypothesis: stationary

选择模型

par(mfrow=c(2, 1))
Acf(dNile)
Pacf(dNile)

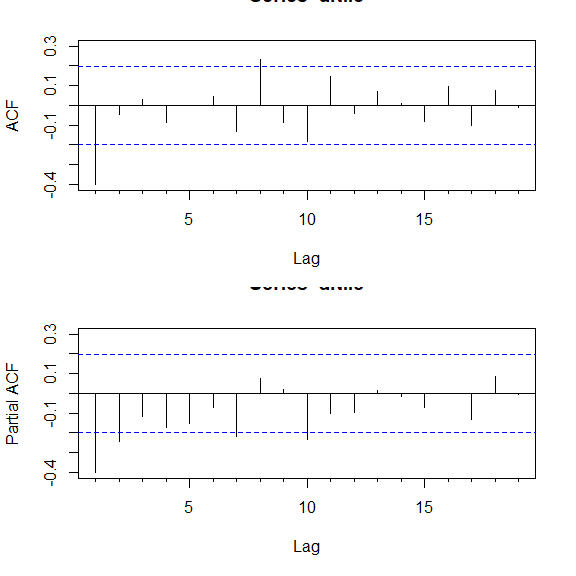
选择 ARIMA 模型的方法

模型	ACF	PACF
ARIMA(p, d, 0)	逐渐减小到 0	在 p 阶后减小到 0
ARIMA(0, d, q)	q 阶后减小到 0	逐渐减小到 0
ARIMA(p, d, q)	逐渐减小到 0	逐渐减小到 0

上述示例中，考虑使用 ARIMA(0, 1, 1) 模型

拟合模型

fit <- arima(
  Nile,
  order=c(0, 1, 1)
)
fit

Call:
arima(x = Nile, order = c(0, 1, 1))

Coefficients:
          ma1
      -0.7329
s.e.   0.1143

sigma^2 estimated as 20600:  log likelihood = -632.55,  aic = 1269.09

AIC值越小越好

accuracy(fit)

                   ME     RMSE      MAE       MPE     MAPE     MASE      ACF1
Training set -11.9358 142.8071 112.1752 -3.574702 12.93594 0.841824 0.1153593

模型评价

模型的残差应该满足独立正态分布

qqnorm(fit$residuals)
qqline(fit$residuals)

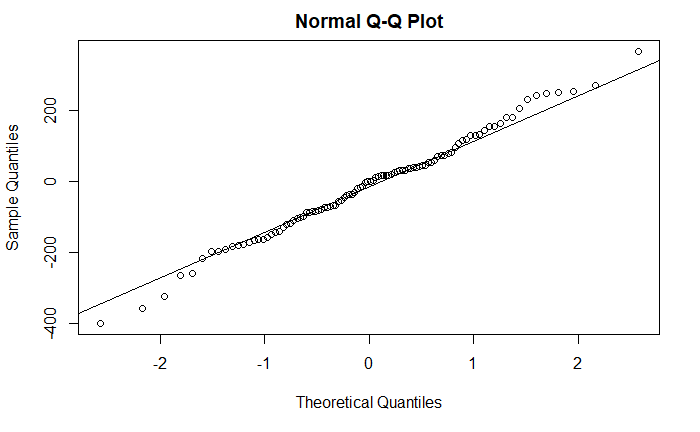
Box.test() 函数检验自相关系数是否都为 0

Box.test(fit$residuals, type="Ljung-Box")

	Box-Ljung test

data:  fit$residuals
X-squared = 1.3711, df = 1, p-value = 0.2416

没通过显著性检验，可以认为残差的自相关系数为零

预测

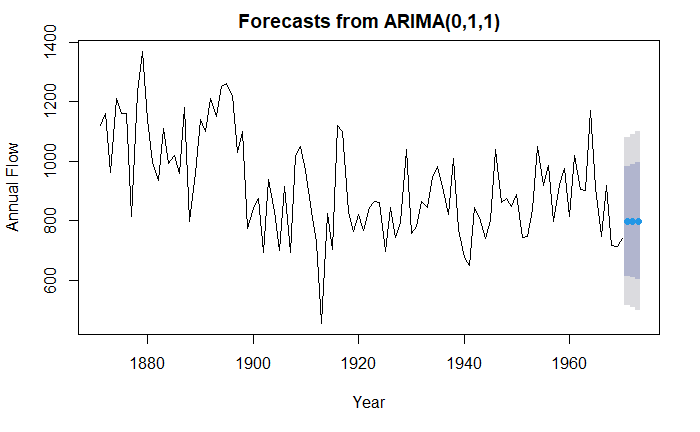
forecast(fit, 3)

     Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
1971       798.3673 614.4307 982.3040 517.0605 1079.674
1972       798.3673 607.9845 988.7502 507.2019 1089.533
1973       798.3673 601.7495 994.9851 497.6663 1099.068

plot(
  forecast(fit, 3),
  xlab="Year",
  ylab="Annual Flow"
)

ARIMA 的自动预测

auto.arima() 函数

fit <- auto.arima(sunspots)
fit

Series: sunspots 
ARIMA(2,1,2) 

Coefficients:
         ar1      ar2      ma1     ma2
      1.3467  -0.3963  -1.7710  0.8103
s.e.  0.0303   0.0287   0.0205  0.0194

sigma^2 estimated as 243.8:  log likelihood=-11745.5
AIC=23500.99   AICc=23501.01   BIC=23530.71

forecast(fit, 3)

         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
Jan 1984       40.43784 20.42717 60.44850 9.834167 71.04150
Feb 1984       41.35311 18.26341 64.44281 6.040458 76.66576
Mar 1984       39.79670 15.23663 64.35677 2.235319 77.35808

accuracy(fit)

                      ME     RMSE      MAE MPE MAPE      MASE        ACF1
Training set -0.02672716 15.60055 11.02575 NaN  Inf 0.4775401 -0.01055012

参考

https://github.com/perillaroc/r-in-action-study

R 语言实战