ISLR实验:PCR和PLS回归
本文源自《统计学习导论:基于R语言应用》(ISLR) 中《6.7 实验3:PCR 和 PLS 回归》章节
介绍两种降维 (dimension reduction) 方法:
- 主成分回归 (principal components regression, PCR)
- 偏最小二乘 (partial least squares, PLS)
library(ISLR)
library(pls)
数据
棒球数据集,使用若干与棒球运动员上一年比赛成绩相关的变量来预测该运动员的薪水 (Salary)
head(Hitters)
AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits
-Andy Allanson 293 66 1 30 29 14 1 293 66
-Alan Ashby 315 81 7 24 38 39 14 3449 835
-Alvin Davis 479 130 18 66 72 76 3 1624 457
-Andre Dawson 496 141 20 65 78 37 11 5628 1575
-Andres Galarraga 321 87 10 39 42 30 2 396 101
-Alfredo Griffin 594 169 4 74 51 35 11 4408 1133
CHmRun CRuns CRBI CWalks League Division PutOuts Assists
-Andy Allanson 1 30 29 14 A E 446 33
-Alan Ashby 69 321 414 375 N W 632 43
-Alvin Davis 63 224 266 263 A W 880 82
-Andre Dawson 225 828 838 354 N E 200 11
-Andres Galarraga 12 48 46 33 N E 805 40
-Alfredo Griffin 19 501 336 194 A W 282 421
Errors Salary NewLeague
-Andy Allanson 20 NA A
-Alan Ashby 10 475.0 N
-Alvin Davis 14 480.0 A
-Andre Dawson 3 500.0 N
-Andres Galarraga 4 91.5 N
-Alfredo Griffin 25 750.0 A
dim(Hitters)
[1] 322 20
names(Hitters)
[1] "AtBat" "Hits" "HmRun" "Runs" "RBI"
[6] "Walks" "Years" "CAtBat" "CHits" "CHmRun"
[11] "CRuns" "CRBI" "CWalks" "League" "Division"
[16] "PutOuts" "Assists" "Errors" "Salary" "NewLeague"
处理缺失值
sum(is.na(Hitters))
[1] 59
删掉缺失值条目
hitters <- na.omit(Hitters)
dim(hitters)
[1] 263 20
sum(is.na(hitters))
[1] 0
数据集
构造数据集
x <- model.matrix(Salary ~ ., hitters)[, -1]
y <- hitters$Salary
分割数据集
set.seed(1)
train <- sample(1:nrow(x), nrow(x)/2)
test <- (-train)
y_test <- y[test]
主成分回归
主成分分析 (principal components analysis, PCA) 是一种可以从多个变量中得到低维变量的有效方法。
主成分回归 (principal components regression, PCR) 是指构造前 M 个主成分 Z_1,…,Z_M,以这些主成分作为预测变量,用最小二乘拟合线性回归模型。
pls 库中的 pcr() 函数实现主成分回归。
参数说明:
scale=TRUE:变量标准化validation="CV":使用十折交叉验证,计算每个主成分个数对应的交叉验证误差
set.seed(1234)
pcr_fit <- pcr(
Salary ~ .,
data=hitters,
scale=TRUE,
validation="CV"
)
summary() 显示每个主成分个数对应的交叉得分,这里使用均方根误差 (RMSE)
summary() 也给出预测变量的被解释方差百分比 (percentage of variance explained) 和在不同数目成分下响应变量的被解释方差百分比。
summary(pcr_fit)
Data: X dimension: 263 19
Y dimension: 263 1
Fit method: svdpc
Number of components considered: 19
VALIDATION: RMSEP
Cross-validated using 10 random segments.
(Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps
CV 452 353.4 351.8 351.7 349.4 345.4 343.6
adjCV 452 353.0 351.4 351.3 348.9 344.8 342.8
7 comps 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps
CV 343.6 345.3 347.0 349.3 349.4 351.5 355.2
adjCV 342.9 344.4 346.1 348.1 348.0 350.1 353.8
14 comps 15 comps 16 comps 17 comps 18 comps 19 comps
CV 349.4 348.5 339.6 338.7 337.2 339.5
adjCV 347.6 346.8 337.9 336.9 335.4 337.5
TRAINING: % variance explained
1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
X 38.31 60.16 70.84 79.03 84.29 88.63 92.26
Salary 40.63 41.58 42.17 43.22 44.90 46.48 46.69
8 comps 9 comps 10 comps 11 comps 12 comps 13 comps 14 comps
X 94.96 96.28 97.26 97.98 98.65 99.15 99.47
Salary 46.75 46.86 47.76 47.82 47.85 48.10 50.40
15 comps 16 comps 17 comps 18 comps 19 comps
X 99.75 99.89 99.97 99.99 100.00
Salary 50.55 53.01 53.85 54.61 54.61
使用 validationplot() 函数绘制 MSE 图像
validationplot(
pcr_fit,
val.type="MSEP"
)
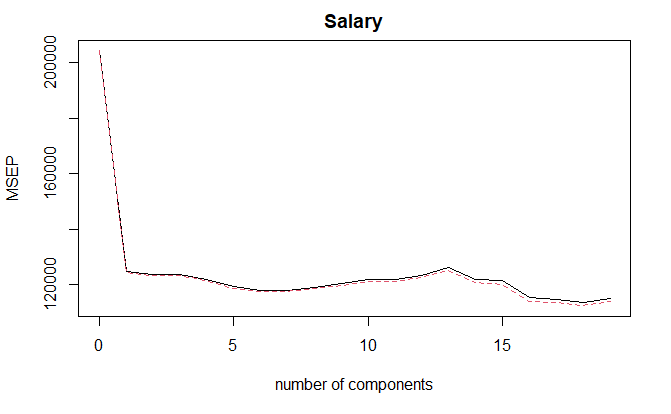
18 个成分时,RMSE 最小。但从 1 个成分开始,RMSE 相差不大,说明仅需要很少的变量就已经足够了。
交叉验证
在训练集上使用交叉验证
set.seed(1234)
pcr_fit <- pcr(
Salary ~ .,
data=hitters,
subset=train,
scale=TRUE,
validation="CV"
)
validationplot(
pcr_fit,
val.type="MSEP"
)
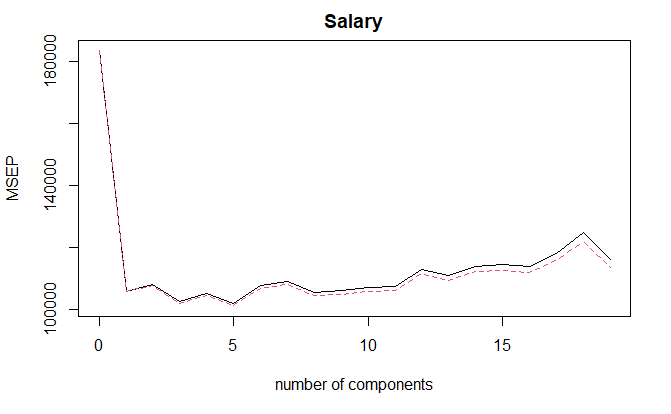
M = 5 时,交叉验证误差最小
计算测试集 MSE
pcr_predict <- predict(
pcr_fit,
x[test,],
ncomp=5
)
mean((pcr_predict - y_test)^2)
[1] 142811.8
拟合
在整个数据集上拟合 PCR 模型
pcr_fit <- pcr(
y ~ x,
scale=TRUE,
ncomp=5
)
summary(pcr_fit)
Data: X dimension: 263 19
Y dimension: 263 1
Fit method: svdpc
Number of components considered: 5
TRAINING: % variance explained
1 comps 2 comps 3 comps 4 comps 5 comps
X 38.31 60.16 70.84 79.03 84.29
y 40.63 41.58 42.17 43.22 44.90
偏最小二乘法
partial least squares, PLS
偏最小二乘法将原始变量的线性组合 Z_1,…,Z_M 作为新的变量集,用这 M 个新变量拟合最小二乘模型。
plsr() 函数
set.seed(1)
pls_fit <- plsr(
Salary ~ .,
data=hitters,
subset=train,
scale=TRUE,
validation="CV"
)
summary(pls_fit)
Data: X dimension: 131 19
Y dimension: 131 1
Fit method: kernelpls
Number of components considered: 19
VALIDATION: RMSEP
Cross-validated using 10 random segments.
(Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps
CV 428.3 325.5 329.9 328.8 339.0 338.9 340.1
adjCV 428.3 325.0 328.2 327.2 336.6 336.1 336.6
7 comps 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps
CV 339.0 347.1 346.4 343.4 341.5 345.4 356.4
adjCV 336.2 343.4 342.8 340.2 338.3 341.8 351.1
14 comps 15 comps 16 comps 17 comps 18 comps 19 comps
CV 348.4 349.1 350.0 344.2 344.5 345.0
adjCV 344.2 345.0 345.9 340.4 340.6 341.1
TRAINING: % variance explained
1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
X 39.13 48.80 60.09 75.07 78.58 81.12 88.21
Salary 46.36 50.72 52.23 53.03 54.07 54.77 55.05
8 comps 9 comps 10 comps 11 comps 12 comps 13 comps 14 comps
X 90.71 93.17 96.05 97.08 97.61 97.97 98.70
Salary 55.66 55.95 56.12 56.47 56.68 57.37 57.76
15 comps 16 comps 17 comps 18 comps 19 comps
X 99.12 99.61 99.70 99.95 100.00
Salary 58.08 58.17 58.49 58.56 58.62
M = 1 时,交叉验证误差最小
计算测试集 MSE
pls_predict <- predict(
pls_fit,
x[test,],
ncomp=1
)
mean((pls_predict - y_test)^2)
[1] 151995.3
拟合
在整个数据集上建立 PLS 模型
pls_fit <- plsr(
Salary ~ .,
data=hitters,
scale=TRUE,
ncomp=1
)
summary(pls_fit)
Data: X dimension: 263 19
Y dimension: 263 1
Fit method: kernelpls
Number of components considered: 1
TRAINING: % variance explained
1 comps
X 38.08
Salary 43.05
PCR 和 PLS 对比
| 方法 | 成分数量 | Salary 被解释方差比 |
|---|---|---|
| PCR | 5 | 44.90 |
| PLS | 1 | 43.05 |
PCR 目的是使预测变量可解释的方差最大化,而 PLS 旨在寻找可以同时解释预测变量和响应变量方差的方向。
参考
https://github.com/perillaroc/islr-study
ISLR实验系列文章
线性回归
分类
重抽样方法
线性模型选择与正则化
