ISLR实验:分类 - 逻辑斯谛回归
本文源自《统计学习导论:基于R语言应用》(ISLR) 中《4.6 R实验:逻辑斯谛回归、LDA、QDA和KNN》章节
library(ISLR)
library(corrgram)
library(car)
library(pROC)
数据
股票市场数据
attach(Smarket)
head(Smarket)
Year Lag1 Lag2 Lag3 Lag4 Lag5 Volume Today Direction
1 2001 0.381 -0.192 -2.624 -1.055 5.010 1.1913 0.959 Up
2 2001 0.959 0.381 -0.192 -2.624 -1.055 1.2965 1.032 Up
3 2001 1.032 0.959 0.381 -0.192 -2.624 1.4112 -0.623 Down
4 2001 -0.623 1.032 0.959 0.381 -0.192 1.2760 0.614 Up
5 2001 0.614 -0.623 1.032 0.959 0.381 1.2057 0.213 Up
6 2001 0.213 0.614 -0.623 1.032 0.959 1.3491 1.392 Up
dim(Smarket)
[1] 1250 9
summary(Smarket)
Year Lag1 Lag2
Min. :2001 Min. :-4.922000 Min. :-4.922000
1st Qu.:2002 1st Qu.:-0.639500 1st Qu.:-0.639500
Median :2003 Median : 0.039000 Median : 0.039000
Mean :2003 Mean : 0.003834 Mean : 0.003919
3rd Qu.:2004 3rd Qu.: 0.596750 3rd Qu.: 0.596750
Max. :2005 Max. : 5.733000 Max. : 5.733000
Lag3 Lag4 Lag5
Min. :-4.922000 Min. :-4.922000 Min. :-4.92200
1st Qu.:-0.640000 1st Qu.:-0.640000 1st Qu.:-0.64000
Median : 0.038500 Median : 0.038500 Median : 0.03850
Mean : 0.001716 Mean : 0.001636 Mean : 0.00561
3rd Qu.: 0.596750 3rd Qu.: 0.596750 3rd Qu.: 0.59700
Max. : 5.733000 Max. : 5.733000 Max. : 5.73300
Volume Today Direction
Min. :0.3561 Min. :-4.922000 Down:602
1st Qu.:1.2574 1st Qu.:-0.639500 Up :648
Median :1.4229 Median : 0.038500
Mean :1.4783 Mean : 0.003138
3rd Qu.:1.6417 3rd Qu.: 0.596750
Max. :3.1525 Max. : 5.733000
探索数据
相关性
cor() 函数计算相关系数矩阵
注:因子变量 Direction 无法计算相关性
cor(Smarket[, -9])
Year Lag1 Lag2 Lag3 Lag4 Lag5
Year 1.00000000 0.029699649 0.030596422 0.033194581 0.035688718 0.029787995
Lag1 0.02969965 1.000000000 -0.026294328 -0.010803402 -0.002985911 -0.005674606
Lag2 0.03059642 -0.026294328 1.000000000 -0.025896670 -0.010853533 -0.003557949
Lag3 0.03319458 -0.010803402 -0.025896670 1.000000000 -0.024051036 -0.018808338
Lag4 0.03568872 -0.002985911 -0.010853533 -0.024051036 1.000000000 -0.027083641
Lag5 0.02978799 -0.005674606 -0.003557949 -0.018808338 -0.027083641 1.000000000
Volume 0.53900647 0.040909908 -0.043383215 -0.041823686 -0.048414246 -0.022002315
Today 0.03009523 -0.026155045 -0.010250033 -0.002447647 -0.006899527 -0.034860083
Volume Today
Year 0.53900647 0.030095229
Lag1 0.04090991 -0.026155045
Lag2 -0.04338321 -0.010250033
Lag3 -0.04182369 -0.002447647
Lag4 -0.04841425 -0.006899527
Lag5 -0.02200231 -0.034860083
Volume 1.00000000 0.014591823
Today 0.01459182 1.000000000
corrgram 包的 corrgram() 函数绘制相关图
corrgram(
Smarket[, -9],
lower.panel=panel.shade,
upper.panel=panel.pie,
text.panel=panel.txt
)
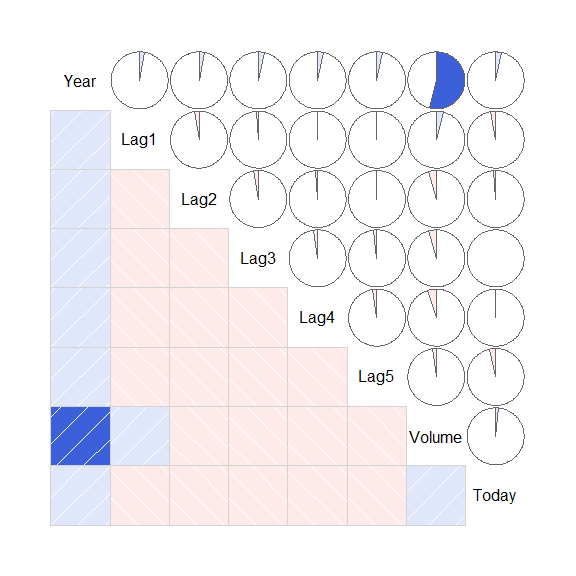
前几日投资回报率 (Lag1 - Loag5) 与当日回报率 (Today) 之间的相关系数接近于 0。
唯一有较大相关性的是 Year 与 Volume,因为 Volume 随 Year 增加而增长
scatterplot(
1:length(Volume),
Volume,
xlab="Index",
ylab="Volume",
boxplots=FALSE
)
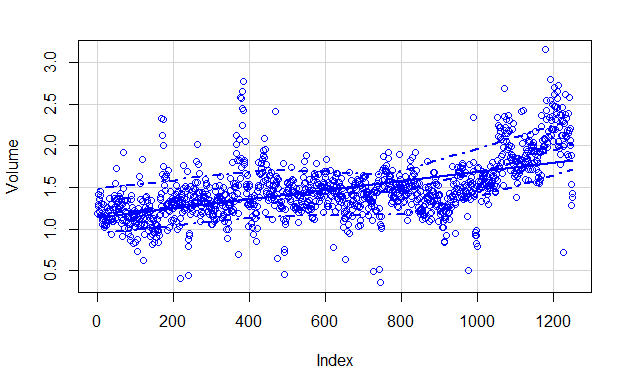
模型
glm() 函数用于拟合 广义线性模型 (generalized linear model)
family=binomial 使用逻辑斯谛回归
glm_fit <- glm(
Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume,
data=Smarket,
family=binomial
)
summary(glm_fit)
Call:
glm(formula = Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 +
Volume, family = binomial, data = Smarket)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.446 -1.203 1.065 1.145 1.326
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.126000 0.240736 -0.523 0.601
Lag1 -0.073074 0.050167 -1.457 0.145
Lag2 -0.042301 0.050086 -0.845 0.398
Lag3 0.011085 0.049939 0.222 0.824
Lag4 0.009359 0.049974 0.187 0.851
Lag5 0.010313 0.049511 0.208 0.835
Volume 0.135441 0.158360 0.855 0.392
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1731.2 on 1249 degrees of freedom
Residual deviance: 1727.6 on 1243 degrees of freedom
AIC: 1741.6
Number of Fisher Scoring iterations: 3
p 值均比较大,说明没有充分证据表明预测变量与 Direction 之间有确切的关联
系数
coef() 函数获取系数
coef(glm_fit)
(Intercept) Lag1 Lag2 Lag3 Lag4
-0.126000257 -0.073073746 -0.042301344 0.011085108 0.009358938
Lag5 Volume
0.010313068 0.135440659
summary() 的结果可以获取更详细的信息,包括系数的 p 值
summary(glm_fit)$coef
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.126000257 0.24073574 -0.5233966 0.6006983
Lag1 -0.073073746 0.05016739 -1.4565986 0.1452272
Lag2 -0.042301344 0.05008605 -0.8445733 0.3983491
Lag3 0.011085108 0.04993854 0.2219750 0.8243333
Lag4 0.009358938 0.04997413 0.1872757 0.8514445
Lag5 0.010313068 0.04951146 0.2082966 0.8349974
Volume 0.135440659 0.15835970 0.8552723 0.3924004
summary(glm_fit)$coef[,4]
(Intercept) Lag1 Lag2 Lag3 Lag4
0.6006983 0.1452272 0.3983491 0.8243333 0.8514445
Lag5 Volume
0.8349974 0.3924004
预测
predict() 函数用于预测
type="response" 表示输出概率 P(Y=1 | X)
glm_probs <- predict(
glm_fit,
type="response"
)
glm_probs[1:10]
1 2 3 4 5 6
0.5070841 0.4814679 0.4811388 0.5152224 0.5107812 0.5069565
7 8 9 10
0.4926509 0.5092292 0.5176135 0.4888378
1 表示 Up,即上涨
contrasts(Direction)
Up
Down 0
Up 1
将概率转换为类别
glm_predict <- rep("Down", 1250)
glm_predict[glm_probs > 0.5] = "Up"
table() 函数生成混淆矩阵,列联表
| 预测- | 预测+ | ||
|---|---|---|---|
| 真实- | 真阴性值 TN | 假阳性值 FP | N |
| 真实+ | 假阳性值 FN | 真阳性值 TP | P |
| N* | P* |
glm_predict_table <- table(
glm_predict,
Direction
)
glm_predict_table
Direction
glm_predict Down Up
Down 145 141
Up 457 507
addmargins(glm_predict_table)
Direction
glm_predict Down Up Sum
Down 145 141 286
Up 457 507 964
Sum 602 648 1250
计算正确率
(TF + TP) / (F + P)
(507+145) / 1250
[1] 0.5216
mean(glm_predict == Direction)
[1] 0.5216
ROC 曲线
pROC 包的 roc() 函数
plot(
roc(
Direction,
glm_probs
),
print.auc=TRUE,
plot=TRUE,
main="ROC Curve for Lag[1-5]"
)
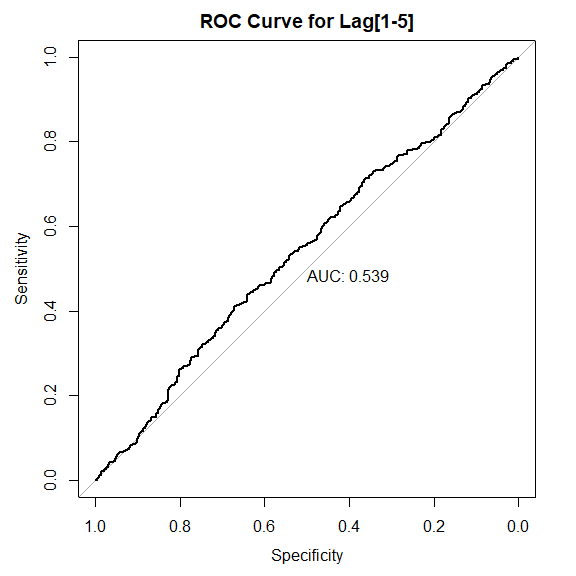
AUC 值很接近 0.5,与随机猜想效果差不多。
训练集与测试集
训练集:2001 至 2004 年
测试集:2005 年
train <- (Year < 2005)
train 是一个布尔变量,Boolean vector
smarket_2005 <- Smarket[!train, ]
dim(smarket_2005)
[1] 252 9
direction_2005 <- Direction[!train]
使用 subset 参数拟合子集
glm_train_fit <- glm(
Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume,
data=Smarket,
subset=train,
family=binomial
)
summary(glm_train_fit)
Call:
glm(formula = Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 +
Volume, family = binomial, data = Smarket, subset = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.302 -1.190 1.079 1.160 1.350
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.191213 0.333690 0.573 0.567
Lag1 -0.054178 0.051785 -1.046 0.295
Lag2 -0.045805 0.051797 -0.884 0.377
Lag3 0.007200 0.051644 0.139 0.889
Lag4 0.006441 0.051706 0.125 0.901
Lag5 -0.004223 0.051138 -0.083 0.934
Volume -0.116257 0.239618 -0.485 0.628
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1383.3 on 997 degrees of freedom
Residual deviance: 1381.1 on 991 degrees of freedom
AIC: 1395.1
Number of Fisher Scoring iterations: 3
预测 2005 年数据
glm_2005_probs <- predict(
glm_train_fit,
smarket_2005,
type="response"
)
使用 50% 作为阈值
glm_2005_predict <- rep("Down", 252)
glm_2005_predict[glm_2005_probs > .5] = "Up"
table(glm_2005_predict, direction_2005)
direction_2005
glm_2005_predict Down Up
Down 77 97
Up 34 44
mean(glm_2005_predict == direction_2005)
[1] 0.4801587
mean(glm_2005_predict != direction_2005)
[1] 0.5198413
比随机猜想更糟糕!
ROC 曲线
plot(
roc(
direction_2005,
glm_2005_probs
),
print.auc=TRUE,
plot=TRUE,
main="ROC Curve for Lag[1-5] on test set"
)
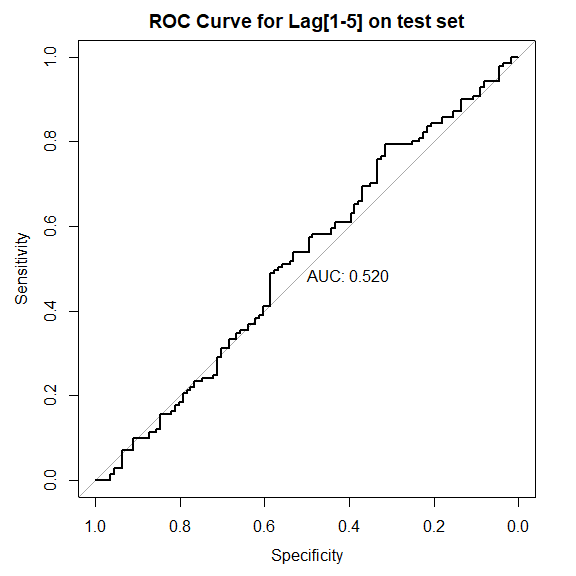
使用更少的变量
仅使用 Lag1 和 Lag2
glm_train_fit_v2 <- glm(
Direction ~ Lag1 + Lag2,
data=Smarket,
subset=train,
family=binomial
)
summary(glm_train_fit_v2)
Call:
glm(formula = Direction ~ Lag1 + Lag2, family = binomial, data = Smarket,
subset = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.345 -1.188 1.074 1.164 1.326
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.03222 0.06338 0.508 0.611
Lag1 -0.05562 0.05171 -1.076 0.282
Lag2 -0.04449 0.05166 -0.861 0.389
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1383.3 on 997 degrees of freedom
Residual deviance: 1381.4 on 995 degrees of freedom
AIC: 1387.4
Number of Fisher Scoring iterations: 3
测试集性能
glm_2005_probs_v2 <- predict(
glm_train_fit_v2,
smarket_2005,
type="response"
)
glm_2005_predict_v2 <- rep("Down", 252)
glm_2005_predict_v2[glm_2005_predict_v2 > .5] = "Up"
table(glm_2005_predict_v2, direction_2005)
direction_2005
glm_2005_predict_v2 Down Up
Up 111 141
mean(glm_2005_predict_v2 == direction_2005)
[1] 0.5595238
准确率
mean(glm_2005_predict_v2 != direction_2005)
[1] 0.4404762
预测阳性率
106/(106+76)
[1] 0.5824176
ROC 曲线
plot(
roc(
direction_2005,
glm_2005_probs_v2
),
print.auc=TRUE,
plot=TRUE,
main="ROC Curve for Lag1 + Lag2"
)
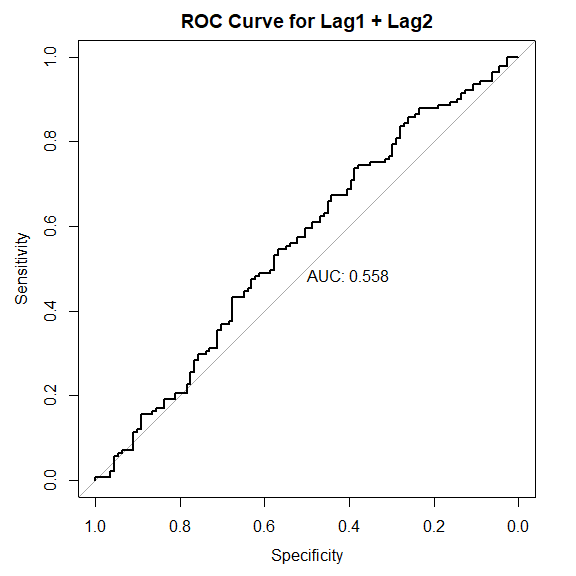
预测效果略有改善,但仍和随机猜想效果差不多。
参考
https://github.com/perillaroc/islr-study
ISLR实验系列文章
线性回归
分类
重抽样方法
线性模型选择与正则化
