ISLR习题:线性回归 - 线性模型的随机误差
目录
本文源自《统计学习导论:基于R语言应用》(ISLR) 第三章习题
向量 x,eps
set.seed(1)
x <- rnorm(100, 0, 1)
eps <- rnorm(100, 0, 0.25)
生成向量 y
y <- -1 + 0.25 * x + eps
其中
- beta_0 = -1
- beta_1 = 0.25
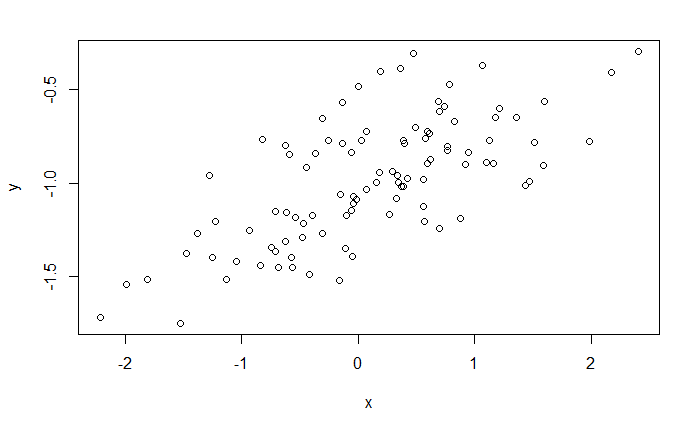
散点图
plot(x, y)
线性拟合
lm_fit_v1 <- lm(y ~ x)
summary(lm_fit_v1)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.46921 -0.15344 -0.03487 0.13485 0.58654
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.00942 0.02425 -41.631 < 2e-16 ***
x 0.24973 0.02693 9.273 4.58e-15 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2407 on 98 degrees of freedom
Multiple R-squared: 0.4674, Adjusted R-squared: 0.4619
F-statistic: 85.99 on 1 and 98 DF, p-value: 4.583e-15
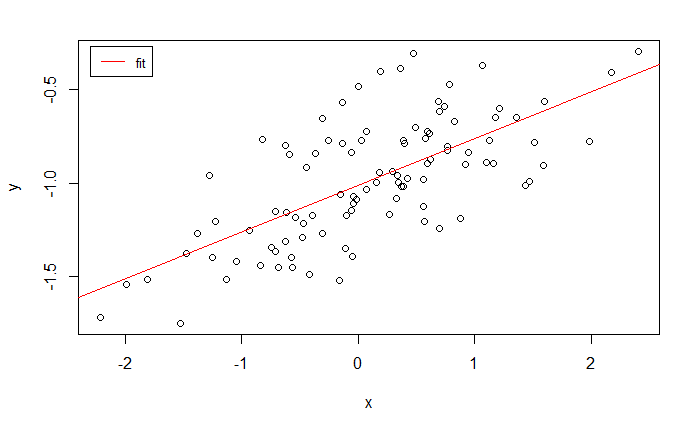
拟合得到的系数与真实值比较接近
拟合线
plot(x, y)
abline(lm_fit_v1, col="red")
legend(
"topleft",
inset=.02,
legend=c("fit"),
col=c("red"),
lty=1:2,
cex=0.8
)
多项式拟合
lm_fit_v2 <- lm(y ~ x + I(x^2))
summary(lm_fit_v2)
Call:
lm(formula = y ~ x + I(x^2))
Residuals:
Min 1Q Median 3Q Max
-0.4913 -0.1563 -0.0322 0.1451 0.5675
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.98582 0.02941 -33.516 < 2e-16 ***
x 0.25429 0.02700 9.420 2.4e-15 ***
I(x^2) -0.02973 0.02119 -1.403 0.164
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2395 on 97 degrees of freedom
Multiple R-squared: 0.4779, Adjusted R-squared: 0.4672
F-statistic: 44.4 on 2 and 97 DF, p-value: 2.038e-14
虽然残差标准误有所降低,但 x^2 项的 p 值太大,没有显著性。
低噪声
set.seed(1)
x <- rnorm(100)
eps <- rnorm(100, 0, 0.01)
y <- -1 + 0.5 * x + eps
plot(x, y)
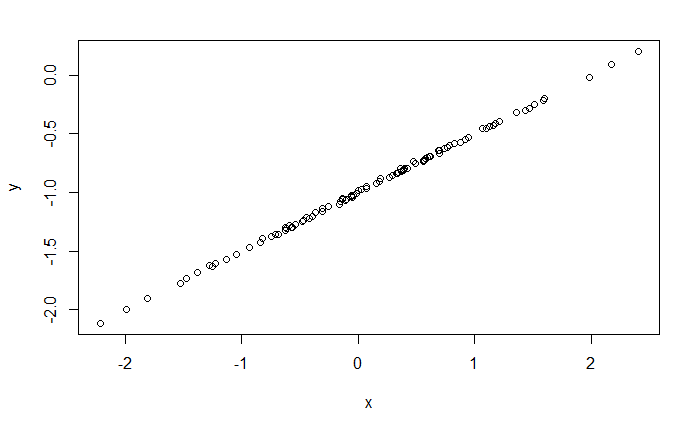
lm_fit_v3 <- lm(y ~ x)
summary(lm_fit_v3)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.018768 -0.006138 -0.001395 0.005394 0.023462
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.0003769 0.0009699 -1031.5 <2e-16 ***
x 0.4999894 0.0010773 464.1 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.009628 on 98 degrees of freedom
Multiple R-squared: 0.9995, Adjusted R-squared: 0.9995
F-statistic: 2.154e+05 on 1 and 98 DF, p-value: < 2.2e-16
plot(x, y)
abline(lm_fit_v3, col="red")
legend(
"topleft",
inset=.02,
legend=c("fit"),
col=c("red"),
lty=1:2,
cex=0.8
)
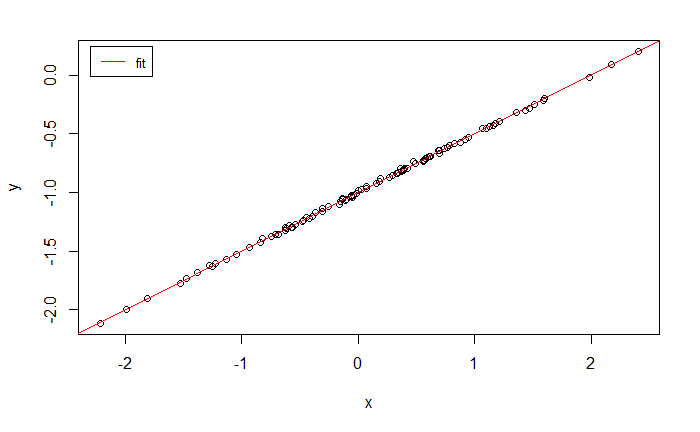
高噪声
set.seed(1)
x <- rnorm(100)
eps <- rnorm(100, 0, 1.0)
y <- -1 + 0.5 * x + eps
plot(x, y)
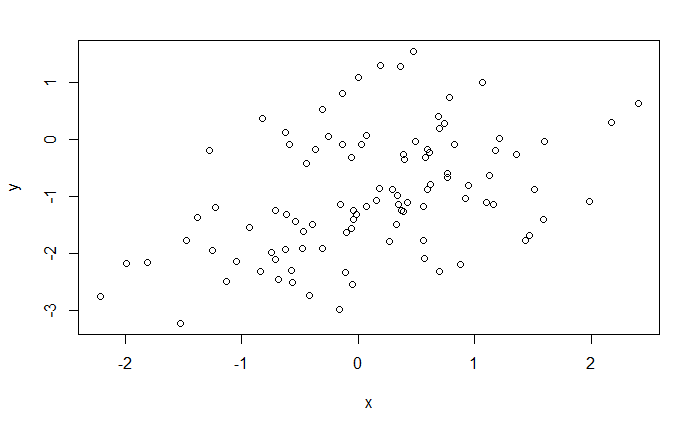
lm_fit_v4 <- lm(y ~ x)
summary(lm_fit_v4)
plot(x, y)
abline(lm_fit_v4, col="red")
legend("topleft", inset=.02, legend=c("fit"), col=c("red"), lty=1:2, cex=0.8)
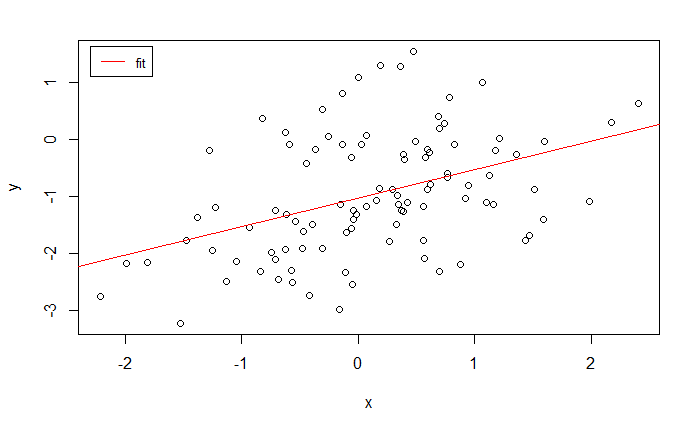
对比
求置信区间
原始数据集
confint(lm_fit_v1)
2.5 % 97.5 %
(Intercept) -1.0575402 -0.9613061
x 0.1962897 0.3031801
低噪声数据集
confint(lm_fit_v3)
2.5 % 97.5 %
(Intercept) -1.0023016 -0.9984522
x 0.4978516 0.5021272
高噪声数据集
confint(lm_fit_v4)
2.5 % 97.5 %
(Intercept) -1.2301607 -0.8452245
x 0.2851588 0.7127204
置信区间随着噪声的增大而增大
参考
https://github.com/perillaroc/islr-study
ISLR实验系列文章
线性回归
分类
重抽样方法
线性模型选择与正则化
