学习R语言：数学运算与模拟

October 26, 2020 (最后修改: November 04, 2020)

programming/R

本文内容来自《R 语言编程艺术》(The Art of R Programming)，有部分修改

R 内置很多数学函数和统计分布函数。

数学函数

exp()
log()
log10()
sqrt()
abs()
sin()，cos() 等三角函数
min()，max()：向量的最小、最大值
which.min()，which.max()：向量的最小、最大元素的位置索引
pmin()，pmax()：多个向量逐元素对比
sum()，prod()
cumsum()，cumprod()
round()，floor()，ceiling()
factorial()：阶乘

扩展示例：计算概率

假设有 n 个独立事件，其中第 i 个时间的发生概率是 P_i，求恰好有一个事件发生的概率。

$$ \sum_{i=1}^{n} p_i(1 - p1)…(1-p_{i-1})(1 - p_{i+1})…(1-p_n) $$

向量 p 包含所有事件的概率 P_i，exactly.one() 函数计算只有一个事件发生的概率

exactly.one <- function(p) {
  not.p <- 1 - p
  total <- 0.0
  for (i in 1:length(p)) {
    total <- total + p[i] * prod(not.p[-i])
  }
  return(total)
}

共有三个事件，概率如下：

p <- c(0.1, 0.2, 0.3)

计算只有一个事件发生的概率

exactly.one(p)

[1] 0.398

累积和与累积乘积

x <- c(12, 5, 13)

cumsum(x)

[1] 12 17 30

cumprod(x)

[1]  12  60 780

最大值和最小值

z <- matrix(
  c(
    1, 5, 6,
    2, 3, 2
  ),
  ncol=2
)
z

     [,1] [,2]
[1,]    1    2
[2,]    5    3
[3,]    6    2

min() 返回全局最小值

min(z[,1], z[,2])

[1] 1

pmin() 比较按位置比较多个参数中每个元素

pmin(z[,1], z[,2])

[1] 1 3 2

pmin(z[1,], z[2,], z[3,])

[1] 1 2

使用 nlm() 和 optim() 求函数的最小、最大值

nlm(
  function(x) {
    return(x^2 - sin(x))
  },
  8
)

$minimum
[1] -0.2324656

$estimate
[1] 0.4501831

$gradient
[1] 4.024558e-09

$code
[1] 1

$iterations
[1] 5

微积分

符号微分

$$ \frac {d} {dx}e^{x^2} = 2xe^{x^2} $$

D(expression(exp(x^2)), "x")

exp(x^2) * (2 * x)

数值积分

$$ \int_{0}^{1} X^2dx \approx 0.3333333 $$

integrate(function(x) x^2, 0, 1)

0.3333333 with absolute error < 3.7e-15

统计分布函数

统计分布函数有一套统一的前缀：

d 对应概率密度函数或概率质量函数
p 对应累计分布函数
q 对应分布的分位数
r 对应随机数生成函数

分布	概率密度函数/概率质量函数	累计分布函数	分位数	随机数
正态分布	dnorm()	pnorm()	qnorm()	rnorm()
卡方分布	dchisq()	pchisq()	qchisq()	rchisq()
二项分布	dbinom()	pbinom()	qbinom()	rbinom()

mean(rchisq(1000, df=2))

[1] 1.959838

qchisq(0.95, 2)

[1] 5.991465

d，p，q 系列函数第一个参数可以是向量，返回多个值

qchisq(c(0.5, 0.95), df=2)

[1] 1.386294 5.991465

排序

`sort()`

x <- c(13, 5, 12, 5)
sort(x)

[1]  5  5 12 13

`order`

order() 函数返回排序后的值在原向量中的索引

order(x)

[1] 2 4 3 1

对数据框排序

y <- data.frame(
  V1=c("def", "ab", "zzzz"),
  V2=c(2, 5, 1)
)
y

r <- order(y$V2)
r

[1] 3 1 2

z <- y[r,]
z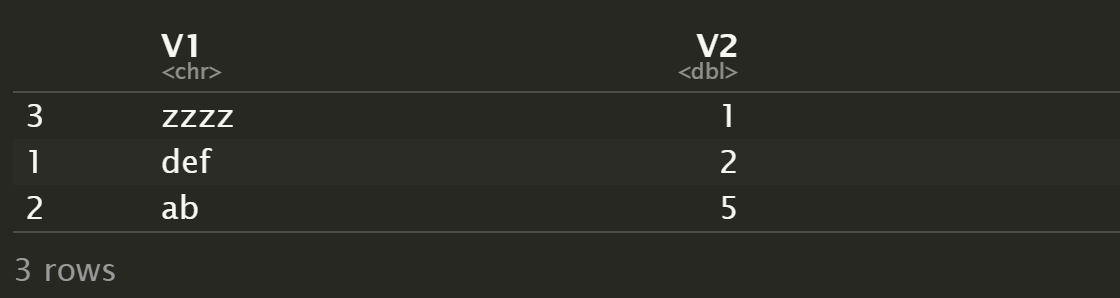

对字符串变量排序

d <- data.frame(
  kids=c("Jack", "Jill", "Billy"),
  ages=c(12, 10, 13)
)
d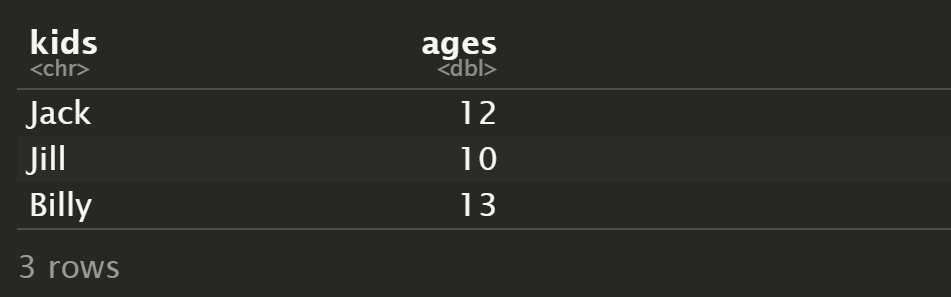

d[order(d$kids),]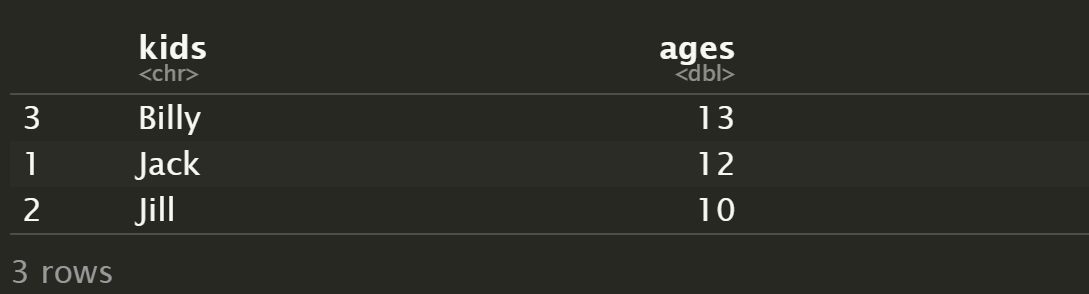

d[order(d$ages),]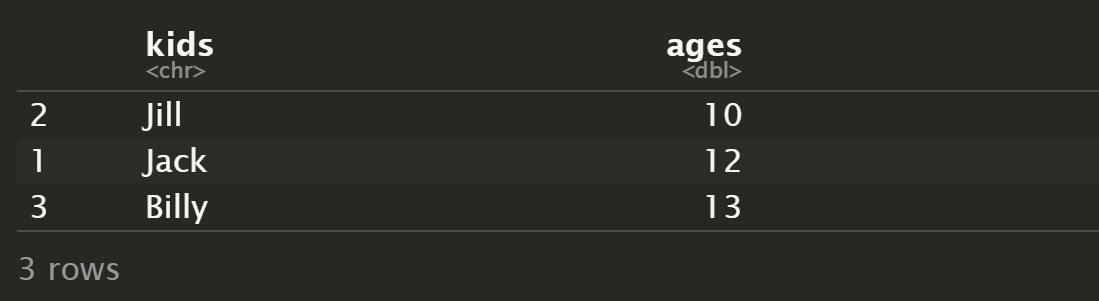

`rank()`

rank() 返回向量中每一个元素的排位 (rank)

x <- c(13, 5, 12, 5)
rank(x)

[1] 4.0 1.5 3.0 1.5

注：小数表示有并列排序

向量和矩阵的线性代数运算

向量

向量 * 标量

y <- c(1, 3, 4, 10)
2 * y

[1]  2  6  8 20

crossprod() 计算向量的点积

crossprod(1:3, c(5, 12, 13))

     [,1]
[1,]   68

矩阵

矩阵乘法

矩阵乘法 %*%

a <- matrix(c(1, 3, 2, 4), nrow=2)
a

     [,1] [,2]
[1,]    1    2
[2,]    3    4

b <- matrix(c(1, 0, -1, 1), nrow=2)
b

     [,1] [,2]
[1,]    1   -1
[2,]    0    1

a %*% b

     [,1] [,2]
[1,]    1    1
[2,]    3    1

`solve()`

solve() 可以解线性方程组，包括求矩阵的逆矩阵

$$ x_1 + x_2 = 2 \ -x_1 + x_2 = 4 $$

$$ \begin{pmatrix} 1 & 1 \\ -1 & 1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

a <- matrix(
  c(1, 1, -1, 1), 
  nrow=2, 
  ncol=2
)
b <- c(2, 4)
solve(a, b)

[1] 3 1

省略第二个参数就是求矩阵的逆矩阵

solve(a)

     [,1] [,2]
[1,]  0.5  0.5
[2,] -0.5  0.5

线性代数运算函数

t()：矩阵转置
qr()：QR 分解
chol()：Cholesky 分解
det()：矩阵的行列式值
eigen()：矩阵的特征值和特征向量
diag()：对角矩阵
sweep()：数值分析批量运算符

`diag()`

返回对角向量

m <- matrix(
  c(1, 7, 2, 8),
  nrow=2
)
m

     [,1] [,2]
[1,]    1    2
[2,]    7    8

dm <- diag(m)
dm

[1] 1 8

从向量构造对角矩阵

diag(dm)

     [,1] [,2]
[1,]    1    0
[2,]    0    8

构造单位矩阵

diag(3)

     [,1] [,2] [,3]
[1,]    1    0    0
[2,]    0    1    0
[3,]    0    0    1

`sweep()`

sweep() 支持复杂的运算

对于 3x3 的矩阵，第一行加 1，第二行加 4，第三行加 7

m <- matrix(
  1:9, 
  nrow=3, 
  byrow=TRUE
)
m

     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9

sweep(
  m,
  1,
  c(1, 4, 7),
  "+"
)

     [,1] [,2] [,3]
[1,]    2    3    4
[2,]    8    9   10
[3,]   14   15   16

参数：

数组
方向
执行函数的参数
执行函数

扩展示例：向量叉积

(x_1, x_2, x_3) 和 (y_1, y_2, y_3) 的叉积：

$$ (x_2y_3 - x_3y_2, -x_1y_3 + x_3y_1, x_1y_2 - x_2y_1) $$

相当于按第一行做行列式展开，其中第一行是占位符

$$ \begin{pmatrix} - & - & - \\ x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \end{pmatrix} $$

xprod <- function(x, y) {
  m <- rbind(rep(NA, 3), x, y)
  xp <- vector(length=3)
  for (i in 1:3) {
    xp[i] <- -(-1)^i * det(m[2:3, -i])
  }
  return(xp)
}

x <- 1:3
y <- 4:6
xprod(x, y)

[1] -3  6 -3

扩展示例：确定马尔科夫链的平稳分布

重复投掷硬币，累计连续三次抛出正面。

设 i 为到目前为止连续抛出正面的次数，取值可以是 0，1 或 2。当连续三次抛出正面时，状态回到 0。

P_ij 是转移概率，从状态 i 转移到状态 j 的概率。

为了统计方便，使用 1，2，3 表示状态 0，1，2。转移矩阵可以表示为

p <- matrix(
  c(
    0.5, 0.5, 0,
    0.5, 0, 0.5,
    1, 0, 0
  ),
  nrow=3,
  byrow=T
)
p

     [,1] [,2] [,3]
[1,]  0.5  0.5  0.0
[2,]  0.5  0.0  0.5
[3,]  1.0  0.0  0.0

假设 pi 是长期状态的概率，需要满足

$$ \pi = \pi P $$

即

$$ (I - P^T)\pi = 0 $$

上述方程组中有一个冗余的等式，可以去掉最后一行。

但还需要满足如下的约束条件

$$ \sum_i \pi_i = 1 $$

换成矩阵形式

$$ 1_n^T \pi = 1 $$

将其放入等式的最后一行，形成新的方程组。

find.pi.v1 <- function(p) {
  n <- nrow(p)
  
  imp <- diag(n) - t(p)
  imp[n,] <- rep(1, n)
  
  rhs <- c(rep(0, n-1), 1)
  pivec <- solve(imp, rhs)
  return(pivec)
}

find.pi.v1(p)

[1] 0.5714286 0.2857143 0.1428571

方案 2 使用特征向量

pi 是矩阵 P 的左特征向量，对应的特征值是 1

find.pi.v2 <- function(p){
  n <- nrow(p)
  
  pivec <- Re(eigen(t(p))$vectors[,1])
  
  if (pivec[1] < 0) pivec <- -pivec
  
  pivec <- pivec / sum(pivec)
  
  return (pivec)
}

find.pi.v2(p)

[1] 0.5714286 0.2857143 0.1428571

集合运算

union(x, y)：并集

x <- c(1, 2, 5)
y <- c(5, 1, 8, 9)
union(x, y)

[1] 1 2 5 8 9

intersect(x, y)：交集

intersect(x, y)

[1] 1 5

setdiff(x, y)：差集

setdiff(x, y)

[1] 2

setdiff(y, x)

[1] 8 9

setequal(x, y)：相等

setequal(x, y)

[1] FALSE

setequal(x, c(1, 2, 5))

[1] TRUE

c %in% y：成员

2 %in% x

[1] TRUE

2 %in% y

[1] FALSE

choose(n, k)：从 n 个元素的集合中选取 k 个元素的子集的数目，即计算组合

choose(5, 2)

[1] 10

对称差

symdiff <- function(a, b) {
  sdfxy <- setdiff(x, y)
  sdfyx <- setdiff(y, x)
  return(union(sdfxy, sdfyx))
}

symdiff(x, y)

[1] 2 8 9

创建二元运算符，计算集合 u 是否是另一个集合 v 的子集

"%subsetof%" <- function(u, v) {
  return(setequal(intersect(u, v), u))
}

c(3, 8) %subsetof% 1:10

[1] TRUE

c(3, 8) %subsetof% 5:10

[1] FALSE

combn()：产生集合元素的组合，输出结果按列排序

c32 <- combn(1:3, 2)
c32

     [,1] [,2] [,3]
[1,]    1    1    2
[2,]    2    3    3

class(c32)

[1] "matrix" "array"

也可以指定一个函数

combn(1:3, 2, sum)

[1] 3 4 5

用 R 做模拟

内置的随机变量发生器

rbinom() 生成服从二项分布或伯努利分布的随机变量

投掷硬币五次中至少四次正面朝上的概率

x <- rbinom(100000, 5, 0.5)
mean(x >= 4)

[1] 0.18842

其他函数示例：

rnorm()：正态分布
rexp()：指数分布
runif()：均匀分布
rgamma()：伽玛分布
rpois()：泊松分布

求解 E[max(X, Y)]，即服从标准正态分布 N(0, 1) 的两个独立随机变量 X 和 Y 的最大值的期望值

sum <- 0
nreps <- 100000
for (i in 1:nreps) {
  xy <- rnorm(2)
  sum <- sum + max(xy)
}
sum/nreps

[1] 0.5617129

不使用循环，需要更多的内存

emax <- function(nreps) {
  x <- rnorm(2*nreps)
  maxxy <- pmax(
    x[1:nreps],
    x[(nreps+1):(2*nreps)]
  )
  return (mean(maxxy))
}

emax(100000)

[1] 0.5636743

重复运行时获得相同的随机数流

set.seed()

set.seed(8888)

扩展案例：组合的模拟

从 20 个人中选出人数分别为 3，4，5 的三个委员会，A 和 B 被选入同一个委员会的概率为多大？

sim <- function(nreps) {
  comm.data <- list()
  # 所有模拟共享
  comm.data$count.ab.same.comm <- 0
  
  for (rep in 1:nreps) {
    # 每次模拟的临时变量
    comm.data$whos.left <- 1:20
    comm.data$num.ab.chosen <- 0
    
    comm.data <- choose.comm(comm.data, 5)
    if (comm.data$num.ab.chosen > 0) next
    
    comm.data <- choose.comm(comm.data, 4)
    if (comm.data$num.ab.chose > 0) next
    
    comm.data <- choose.comm(comm.data, 3)
  }
  print(comm.data$count.ab.same.comm / nreps)
}

choose.comm <- function(com.data, com.size) {
  # 抽样
  committee <- sample(com.data$whos.left, com.size)
  
  # 通过交集求个数
  com.data$num.ab.chosen <- length(intersect(1:2, committee))
  if (com.data$num.ab.chosen == 2) {
    com.data$count.ab.same.comm <- com.data$count.ab.same.comm + 1
  }
  
  com.data$whos.left <- setdiff(com.data$whos.left, committee)
  return(com.data)
}