ISLR实验:线性模型扩展
本文源自《统计学习导论:基于R语言应用》(ISLR) 中《3.6 实验:线性回归》章节
标准线性回归模型有两个最重要的假设:
- 可加性 (additive):预测变量 X_j 的变化对响应变量 Y 产生的影响与其他预测变量的取值无关。
- 线性 (linear):无论 X_j 取何值,X_j 变化一个单位引起的响应变量 Y 的变化是恒定的。
上述假设在实际问题中常常被违背。
本文介绍一些扩展的线性模型,继续使用 Boston 数据集。
library(MASS)
library(ISLR)交互项
交互项 (interaction) 去除可加性假设,考虑变量之间的交互作用 (interaction)。
使用两个变量的乘积作为一个交互项。
lm() 支持交互项。
lstat:black 将 lstat 和 black 的交互项加入到模型中。
lstat*age 将 lstat,age 和交互项 lstat * age 作为预测变量,是 lstat + age + lstat:age 的简写
lm.fit.inter <- lm(medv~lstat * age, data=Boston)
lm.fit.interCall:
lm(formula = medv ~ lstat * age, data = Boston)
Coefficients:
(Intercept) lstat age lstat:age
36.0885359 -1.3921168 -0.0007209 0.0041560
summary(lm.fit.inter)Call:
lm(formula = medv ~ lstat * age, data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.806 -4.045 -1.333 2.085 27.552
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 36.0885359 1.4698355 24.553 < 2e-16 ***
lstat -1.3921168 0.1674555 -8.313 8.78e-16 ***
age -0.0007209 0.0198792 -0.036 0.9711
lstat:age 0.0041560 0.0018518 2.244 0.0252 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.149 on 502 degrees of freedom
Multiple R-squared: 0.5557, Adjusted R-squared: 0.5531
F-statistic: 209.3 on 3 and 502 DF, p-value: < 2.2e-16
实验分层原则 (hierarchical principle) 规定:
如果模型中含有交互项,那么即使主效应的系数的 p 值不显著,也应包含在模型中。
虽然上述模型中 age 的 p 值较大,但 age 也应该包含在模型中。
预测变量的非线性变换
一种简单的非线性关系就是 多项式回归 (polynomial regression)。
lm() 函数支持预测变量的非线性变换。
对于预测变量 X,可以使用 I(X^2) 创建预测变量 X^2。
建立 medv 对 lstat 和 lstat^2 的回归
lm.fit.power <- lm(medv~lstat + I(lstat^2), data=Boston)
lm.fit.powerCall:
lm(formula = medv ~ lstat + I(lstat^2), data = Boston)
Coefficients:
(Intercept) lstat I(lstat^2)
42.86201 -2.33282 0.04355
summary(lm.fit.power)Call:
lm(formula = medv ~ lstat + I(lstat^2), data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.2834 -3.8313 -0.5295 2.3095 25.4148
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 42.862007 0.872084 49.15 <2e-16 ***
lstat -2.332821 0.123803 -18.84 <2e-16 ***
I(lstat^2) 0.043547 0.003745 11.63 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.524 on 503 degrees of freedom
Multiple R-squared: 0.6407, Adjusted R-squared: 0.6393
F-statistic: 448.5 on 2 and 503 DF, p-value: < 2.2e-16
二次项的 p 值接近零,表示它使模型得到改进。
验证
使用 anova() 函数量化二次拟合在何种程度上优于线性组合。
lm.fit <- lm(medv~lstat, data=Boston)
summary(lm.fit)Call:
lm(formula = medv ~ lstat, data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.168 -3.990 -1.318 2.034 24.500
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 34.55384 0.56263 61.41 <2e-16 ***
lstat -0.95005 0.03873 -24.53 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.216 on 504 degrees of freedom
Multiple R-squared: 0.5441, Adjusted R-squared: 0.5432
F-statistic: 601.6 on 1 and 504 DF, p-value: < 2.2e-16
anova(lm.fit, lm.fit.power)Analysis of Variance Table
Model 1: medv ~ lstat
Model 2: medv ~ lstat + I(lstat^2)
Res.Df RSS Df Sum of Sq F Pr(>F)
1 504 19472
2 503 15347 1 4125.1 135.2 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
模型 1 是线性模型,模型 2 是包含一次项和二次项的二次模型
anova() 通过假设检验比较两个模型。
- 零假设:这两个模型拟合效果相当
- 备择假设:二次模型效果更优
上述结果中,F 统计量为 135,p 值几乎为 0,表明二次模型远远优于一次模型。
绘图
par(mfrow=c(2, 2))
plot(lm.fit.power)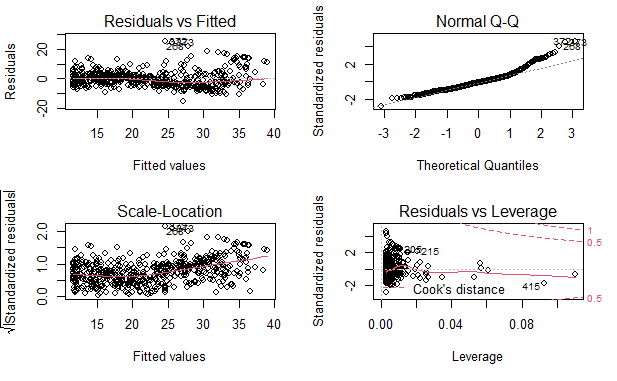
残差中可识别的规律很少
多项式拟合
使用 poly() 和 lm() 可以创建多项式拟合
5 阶多项式拟合
lm.fit.5 <- lm(medv~poly(lstat, 5), data=Boston)
summary(lm.fit.5)Call:
lm(formula = medv ~ poly(lstat, 5), data = Boston)
Residuals:
Min 1Q Median 3Q Max
-13.5433 -3.1039 -0.7052 2.0844 27.1153
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 22.5328 0.2318 97.197 < 2e-16 ***
poly(lstat, 5)1 -152.4595 5.2148 -29.236 < 2e-16 ***
poly(lstat, 5)2 64.2272 5.2148 12.316 < 2e-16 ***
poly(lstat, 5)3 -27.0511 5.2148 -5.187 3.10e-07 ***
poly(lstat, 5)4 25.4517 5.2148 4.881 1.42e-06 ***
poly(lstat, 5)5 -19.2524 5.2148 -3.692 0.000247 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.215 on 500 degrees of freedom
Multiple R-squared: 0.6817, Adjusted R-squared: 0.6785
F-statistic: 214.2 on 5 and 500 DF, p-value: < 2.2e-16
上述结果表明,5 阶以下的多项式改善了模型的效果。
更高阶模型
lm.fit.8 <- lm(medv~poly(lstat, 8), data=Boston)
summary(lm.fit.8)Call:
lm(formula = medv ~ poly(lstat, 8), data = Boston)
Residuals:
Min 1Q Median 3Q Max
-13.7394 -3.1475 -0.7329 2.0959 26.9915
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 22.5328 0.2317 97.233 < 2e-16 ***
poly(lstat, 8)1 -152.4595 5.2129 -29.247 < 2e-16 ***
poly(lstat, 8)2 64.2272 5.2129 12.321 < 2e-16 ***
poly(lstat, 8)3 -27.0511 5.2129 -5.189 3.08e-07 ***
poly(lstat, 8)4 25.4517 5.2129 4.882 1.41e-06 ***
poly(lstat, 8)5 -19.2524 5.2129 -3.693 0.000246 ***
poly(lstat, 8)6 6.5088 5.2129 1.249 0.212404
poly(lstat, 8)7 1.9416 5.2129 0.372 0.709703
poly(lstat, 8)8 -6.7299 5.2129 -1.291 0.197302
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.213 on 497 degrees of freedom
Multiple R-squared: 0.6838, Adjusted R-squared: 0.6787
F-statistic: 134.4 on 8 and 497 DF, p-value: < 2.2e-16
5 阶以上的多项式的 p 值不显著
对数变换
lm() 也支持其他种类的非线性变换,比如对数变换
lm.fit.log <- lm(medv~log(rm), data=Boston)
summary(lm.fit.log)Call:
lm(formula = medv ~ log(rm), data = Boston)
Residuals:
Min 1Q Median 3Q Max
-19.487 -2.875 -0.104 2.837 39.816
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -76.488 5.028 -15.21 <2e-16 ***
log(rm) 54.055 2.739 19.73 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.915 on 504 degrees of freedom
Multiple R-squared: 0.4358, Adjusted R-squared: 0.4347
F-statistic: 389.3 on 1 and 504 DF, p-value: < 2.2e-16
定性预测变量
研究 Carseats 数据集(汽车座椅)。
head(Carseats)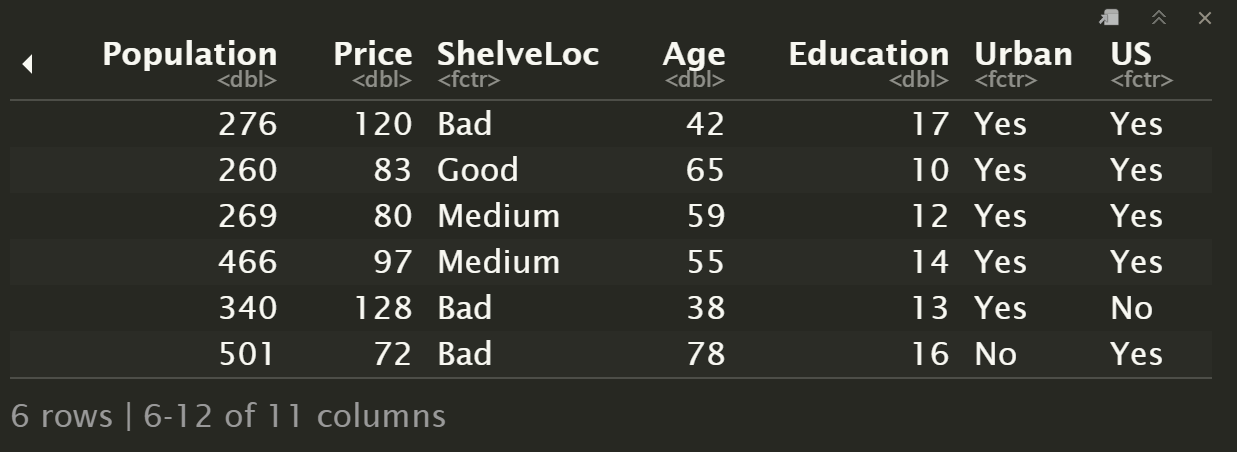
names(Carseats) [1] "Sales" "CompPrice" "Income" "Advertising" "Population" "Price"
[7] "ShelveLoc" "Age" "Education" "Urban" "US"
ShelveLoc 是定性变量,也称为 因子 (factor),表示每个地区搁架位置的质量指标,即在每个地区汽车座椅在商店内的展示空间。 有三个可能的取值,称为 水平 (levels):
- 坏:
Bad - 中等:
Medium - 好:
good
数据集中已指定 ShelveLoc 为 factor 类型,R 将自动生成虚拟变量。
构建一个包含交互项的多元回归模型
lm.fit.factor <- lm(
Sales~.+Income:Advertising + Price:Age,
data=Carseats
)summary(lm.fit.factor)Call:
lm(formula = Sales ~ . + Income:Advertising + Price:Age, data = Carseats)
Residuals:
Min 1Q Median 3Q Max
-2.9208 -0.7503 0.0177 0.6754 3.3413
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.5755654 1.0087470 6.519 2.22e-10 ***
CompPrice 0.0929371 0.0041183 22.567 < 2e-16 ***
Income 0.0108940 0.0026044 4.183 3.57e-05 ***
Advertising 0.0702462 0.0226091 3.107 0.002030 **
Population 0.0001592 0.0003679 0.433 0.665330
Price -0.1008064 0.0074399 -13.549 < 2e-16 ***
ShelveLocGood 4.8486762 0.1528378 31.724 < 2e-16 ***
ShelveLocMedium 1.9532620 0.1257682 15.531 < 2e-16 ***
Age -0.0579466 0.0159506 -3.633 0.000318 ***
Education -0.0208525 0.0196131 -1.063 0.288361
UrbanYes 0.1401597 0.1124019 1.247 0.213171
USYes -0.1575571 0.1489234 -1.058 0.290729
Income:Advertising 0.0007510 0.0002784 2.698 0.007290 **
Price:Age 0.0001068 0.0001333 0.801 0.423812
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.011 on 386 degrees of freedom
Multiple R-squared: 0.8761, Adjusted R-squared: 0.8719
F-statistic: 210 on 13 and 386 DF, p-value: < 2.2e-16
constrasts() 函数返回 R 虚拟变量的编码
contrasts(Carseats$ShelveLoc)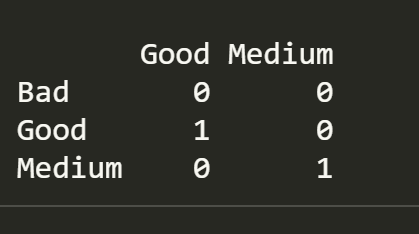
R 创建两个 哑变量 (dummy variable):
ShelveLocGood:值为 1 时表示 GoodShelveLocMedium:值为 1 是表示 Medium
两个变量值均为 0 时,表示 Bad
注意:这两个变量不能同时为 1
回归模型中,ShelveLocGood 系数为正,表明好的货架位置与高销售额相关。
ShelveLocMedium 系数为较小的正值,表明中等水平货架位置的销量比坏位置高,但比一个好位置差。
参考
https://github.com/perillaroc/islr-study
ISLR实验系列文章
线性回归
分类
重抽样方法
线性模型选择与正则化
