AMS机器学习课程:Keras深度学习 - 卷积神经网络
本文翻译自 AMS 机器学习 Python 教程,并有部分修改。
David John Gagne, 2019: “Deep Learning with Keras”.
David John Gagne, National Center for Atmospheric Research
本文接上一篇文章《AMS机器学习课程:Keras深度学习 - 人工神经网络》
数据
为卷积神经网络,我们将加载以每次风暴为中心的空间块 (spatial patches)。
本文数据的下载方法请查阅《AMS机器学习课程:数据分析与预处理》
准备
载入需要使用的库
import numpy as np
import pandas as pd
import xarray as xr
import matplotlib.pyplot as plt
import pathlib
from tqdm.notebook import tqdm路径
创建风暴 netCDF4 文件的列表
start_path = pathlib.Path("../data/track_data_ncar_ams_3km_nc_small")
storm_files = sorted(start_path.glob("*.nc"))
storm_files[:5][WindowsPath('../data/track_data_ncar_ams_3km_nc_small/NCARSTORM_20101024-0000_d01_model_patches.nc'),
WindowsPath('../data/track_data_ncar_ams_3km_nc_small/NCARSTORM_20101122-0000_d01_model_patches.nc'),
WindowsPath('../data/track_data_ncar_ams_3km_nc_small/NCARSTORM_20110201-0000_d01_model_patches.nc'),
WindowsPath('../data/track_data_ncar_ams_3km_nc_small/NCARSTORM_20110308-0000_d01_model_patches.nc'),
WindowsPath('../data/track_data_ncar_ams_3km_nc_small/NCARSTORM_20110326-0000_d01_model_patches.nc')]
定义问题
输入变量
input_vars = [
"REFL_COM_curr",
"U10_curr",
"V10_curr",
]输出变量
output_vars = [
"RVORT1_MAX_future"
]查看数据
首先看一下 NetCDF 文件的内容
storm_file = storm_files[0]
ds = xr.open_dataset(storm_file)
ds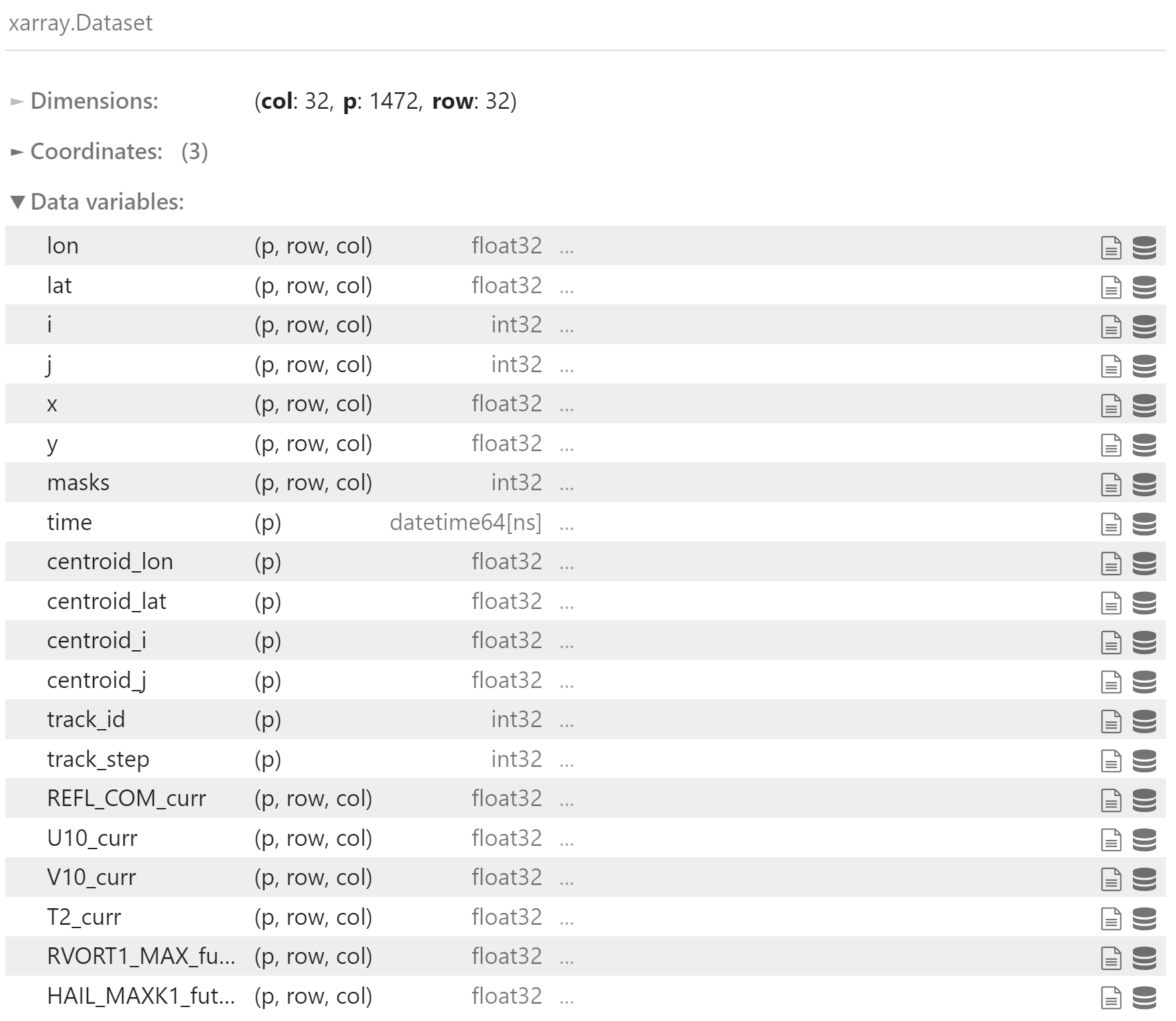
ds.REFL_COM_curr.values.shape(1472, 32, 32)
其中每个 p 代表一个数据块,row 和 col 表示块大小
载入数据
run_times = []
valid_times = []
input_data = []
output_data = []遍历每个风暴文件,提取相关变量
p = tqdm(range(len(storm_files)))
for i in p:
storm_file = storm_files[i]
# 从文件名中提取 run time
run_time = pd.Timestamp(storm_file.name.split("_")[1])
# 载入数据
ds = xr.open_dataset(storm_file)
# 将给定文件中的变量按照 input_vars 中的顺序堆叠
# 生成 (p, row, col, vars) 的数组
input_data.append(
np.stack(
[ds[v].values for v in input_vars],
axis=-1,
)
)
output_data.append(
np.stack(
[ds[v].values for v in output_vars],
axis=-1,
)
)
# 提取 valid times
valid_times.append(ds["time"].values)
# 提取 run times,并与每个块匹配,即为每个块 (维度p) 都设置时间
run_times.append([run_time] * input_data[-1].shape[0])
p.set_description(run_time.strftime("%Y-%m-%d %H:%M:%S"))
# 关闭数据集
ds.close()合并数据
将数据堆叠为一个数组,而不是数组列表
np.vstack 将列表中的数组按行堆叠在一起
all_input_data = np.vstack(input_data)
all_input_data.shape(121137, 32, 32, 3)
all_output_data = np.vstack(output_data)
all_output_data.shape(121137, 32, 32, 1)
all_run_times = np.concatenate(run_times)
all_run_times.shape(121137,)
all_valid_times = np.concatenate(valid_times)
all_valid_times.shape(121137,)
删除所有的数组列表,节省内存
del input_data[:], output_data[:], run_times[:], valid_times[:]
del input_data, output_data, run_times, valid_times数据变换
加载 netCDF 数据后,我们还需要标准化每个输入变量。 为此,我们针对给定变量计算所有网格点上的均值和标准差,然后使用该值重新缩放数据。
normalize_multivariate_data() 函数独立地标准化四维数据矩阵中的每个通道。
参数:
data:四维矩阵,维度:样本, x, y, 通道/变量scaling_values:pandas.DataFrame包含均值和标准差列
返回:
标准化后的数据,scaling_values
def normalize_multivariate_data(
data,
scaling_values=None
):
normed_data = np.zeros(
data.shape,
dtype=data.dtype
)
scale_cols = ["mean", "std"]
# 预申请参数数组
if scaling_values is None:
scaling_values = pd.DataFrame(
np.zeros(
(data.shape[-1], len(scale_cols)),
dtype=np.float32
),
columns=scale_cols
)
# 计算标准化参数,并对数据进行标准化
for i in range(data.shape[-1]):
scaling_values.loc[i, ["mean", "std"]] = [
data[:, :, :, i].mean(),
data[:, :, :, i].std()
]
normed_data[:, :, :, i] = (
data[:, :, :, i] - scaling_values.loc[i, "mean"]
) / scaling_values.loc[i, "std"]
return normed_data, scaling_values以日期 train_test_date 为界,将格点数据分为训练集和测试集,并进行标准化
train_norm_2d, scaling_values = normalize_multivariate_data(
all_input_data[valid_dates < train_test_date],
)
print(scaling_values) mean std
0 22.685513 15.761677
1 -0.290119 4.668883
2 0.843101 5.026216
test_norm_2d, _ = normalize_multivariate_data(
all_input_data[valid_dates >= train_test_date],
scaling_values=scaling_values,
)卷积神经网络
Convolutional Neural Network
全连接神经网络 (Dense neural networks) 对于标量值非常有效,但是如果我们希望神经网络从时间序列或空间场中进行预测该怎么办? 因为为每个输入层和隐藏层之间的每个连接分配了独立的权重,所以权重的数量将急剧增加,并且网络将难以收敛,并且可能会过拟合数据中的噪声。
如果我们对数据做出一些关键假设,则可以大大减少独立权重的数量,提高性能,并减少所需的预处理和特征提取工作量。
关键假设:
- 输入数据具有空间和/或时间结构。
- 感兴趣的结构可以出现在图像内的任何位置。
- 特征发生在多个尺度上。
我们可以通过将我们的数据从标量值表重新配置为一组二维字段,并在其它维度上 (instance, y, x, variable) 堆叠。 然后,我们重新配置神经网络,以使每个神经元仅具有到上一层的本地连接,并且权重以空间模式排列并在网络中共享。 当我们这样做时,我们就开始了卷积神经网络 convolutional neural network 或 CNN。
CNN 遵循全连接神经网络的一般结构,它由一个输入层,一个或多个隐藏层和一个输出层组成。 但是,密集层 (Dense Layers) 已被卷积层 (convolution layers) 取代。 卷积层将一组局部连接的权重应用于输入图像的一部分。 权重乘以输入,然后求和,以在该位置创建输出。 然后,权重在整个图像上移动,然后重复该操作。 卷积的示例如下所示。
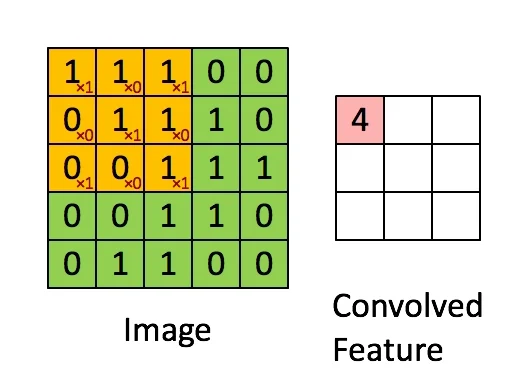
每个卷积滤波器捕获不同种类的特征。
通过某种统计汇总或合并来减少输入数据的空间维数,最容易实现在较大区域上的捕获要素。 通常使用“最大池化 (Max Pooling)”,它在 2x2 窗口内取最大值。 也可以使用平均池化 (Average (Mean) Pooling)。 池化层通常放置在每个卷积层之后。
深度卷积神经网络
现在我们使用 Keras 构建一个简单的多层 CNN
配置
卷积过滤器数目
num_conv_filters = 8卷积过滤器宽度
filter_width = 5卷积层激活函数
conv_activation = "relu"学习率
learning_rate = 0.001构造
输入数据的维度:(instance, y, x, variable)
train_norm_2d.shape(76377, 32, 32, 3)
from tensorflow.compat.v1.keras.layers import Input
conv_net_in = Input(
shape=train_norm_2d.shape[1:]
)第一个 2 维卷积层
from tensorflow.compat.v1.keras.layers import Conv2D
conv_net = Conv2D(
num_conv_filters,
(filter_width, filter_width),
padding="same"
)(conv_net_in)
conv_net = Activation(conv_activation)(conv_net)平均池化 (Average pooling) 选择 2x2 邻域内的平均值,以减少图片尺寸
from tensorflow.compat.v1.keras.layers import AveragePooling2D
conv_net = AveragePooling2D()(conv_net)第二个卷积层和池化层
conv_net = Conv2D(
num_conv_filters * 2,
(filter_width, filter_width),
padding="same"
)(conv_net)
conv_net = Activation(conv_activation)(conv_net)
conv_net = AveragePooling2D()(conv_net)第三个卷积层和池化层
conv_net = Conv2D(
num_conv_filters * 4,
(filter_width, filter_width),
padding="same",
)(conv_net)
conv_net = Activation(conv_activation)(conv_net)
conv_net = AveragePooling2D()(conv_net)将最后一个卷积层展平为长特征向量
from tensorflow.compat.v1.keras.layers import Flatten
conv_net = Flatten()(conv_net)全连接输出层,相当于最后一层是逻辑回归 (logistic regression)
conv_net = Dense(1)(conv_net)
conv_net = Activation("sigmoid")(conv_net)构建模型对象
conv_model = Model(
conv_net_in,
conv_net
)使用默认参数的 Adam 优化器
opt = Adam(lr=learning_rate)编译模型
conv_model.compile(
opt,
"binary_crossentropy"
)模型概述信息
conv_model.summary()Model: "functional_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_2 (InputLayer) [(None, 32, 32, 3)] 0
_________________________________________________________________
conv2d (Conv2D) (None, 32, 32, 8) 608
_________________________________________________________________
activation_8 (Activation) (None, 32, 32, 8) 0
_________________________________________________________________
average_pooling2d (AveragePo (None, 16, 16, 8) 0
_________________________________________________________________
conv2d_1 (Conv2D) (None, 16, 16, 16) 3216
_________________________________________________________________
activation_9 (Activation) (None, 16, 16, 16) 0
_________________________________________________________________
average_pooling2d_1 (Average (None, 8, 8, 16) 0
_________________________________________________________________
conv2d_2 (Conv2D) (None, 8, 8, 32) 12832
_________________________________________________________________
activation_10 (Activation) (None, 8, 8, 32) 0
_________________________________________________________________
average_pooling2d_2 (Average (None, 4, 4, 32) 0
_________________________________________________________________
flatten (Flatten) (None, 512) 0
_________________________________________________________________
dense_2 (Dense) (None, 1) 513
_________________________________________________________________
activation_11 (Activation) (None, 1) 0
=================================================================
Total params: 17,169
Trainable params: 17,169
Non-trainable params: 0
_________________________________________________________________
如果您不想训练自己的模型,可以在下面加载保存的模型。
from tensorflow.compat.v1.keras.models import load_model
conv_model = load_model("ams_cnn_model.h5")训练
使用 fit() 方法训练模型
train_norm_2d.shape(76377, 32, 32, 3)
train_out.shape(76377,)
conv_model.fit(
train_norm_2d,
train_out,
batch_size=512,
epochs=10
)Train on 76377 samples
Epoch 1/10
76377/76377 [==============================] - 21s 281us/sample - loss: 0.1723
Epoch 2/10
76377/76377 [==============================] - 21s 281us/sample - loss: 0.1274
Epoch 3/10
76377/76377 [==============================] - 21s 281us/sample - loss: 0.1147
Epoch 4/10
76377/76377 [==============================] - 21s 281us/sample - loss: 0.1077
Epoch 5/10
76377/76377 [==============================] - 22s 290us/sample - loss: 0.1035
Epoch 6/10
76377/76377 [==============================] - 22s 286us/sample - loss: 0.1018
Epoch 7/10
76377/76377 [==============================] - 22s 284us/sample - loss: 0.1001
Epoch 8/10
76377/76377 [==============================] - 22s 288us/sample - loss: 0.0987
Epoch 9/10
76377/76377 [==============================] - 23s 302us/sample - loss: 0.0977
Epoch 10/10
76377/76377 [==============================] - 23s 307us/sample - loss: 0.0964
检验
让我们在测试集上验证。 CNN 应该比全连接神经网络表现好很多。
def calc_verification_scores(
model,
test_data,
test_labels,
):
predicts = model.predict(test_data, batch_size=1024)
model_auc = roc_auc_score(test_labels, predicts)
model_brier_score = mean_squared_error(test_labels, predicts)
climo_brier_score = mean_squared_error(
test_labels,
np.ones(test_labels.size) * test_labels.sum() / test_labels.size
)
model_brier_skill_score = 1 - model_brier_score / climo_brier_score
print(f"AUC: {model_auc:0.3f}")
print(f"Brier Score: {model_brier_score:0.3f}")
print(f"Brier Score (Climatology): {climo_brier_score:0.3f}")
print(f"Brier Skill Score: {model_brier_skill_score:0.3f}") calc_verification_scores(
conv_model,
test_norm_2d,
test_out
)AUC: 0.956
Brier Score: 0.033
Brier Score (Climatology): 0.050
Brier Skill Score: 0.344
现在,我们将保存我们的神经网络以备后用。
from tensorflow.compat.v1.keras.models import save_model
save_model(conv_model, "ams_cnn_model.h5")参考
https://github.com/djgagne/ams-ml-python-course
AMS 机器学习课程
数据预处理:
《数据分析与预处理》
实际数据处理:
线性回归:
逻辑回归:
决策树:
Keras 深度学习:
