预测雷暴旋转的基础机器学习：分类 - 训练

August 16, 2020 (最后修改: August 22, 2021)

本文翻译自 AMS 机器学习 Python 教程，并有部分修改。
Lagerquist, R., and D.J. Gagne II, 2019: “Basic machine learning for predicting thunderstorm rotation: Python tutorial”. https://github.com/djgagne/ams-ml-python-course/blob/master/module_2/ML_Short_Course_Module_2_Basic.ipynb.

从本文开始，将介绍二元分类问题。

示例数据

关于本文示例数据的详细信息，请参考之前介绍线性回归的系列文章：

《预测雷暴旋转的基础机器学习 - 数据》

二元分类

本模块的其余部分着重于二元分类，而不是回归。 “回归”是对实数的预测（例如，上面我们预测了最大未来涡度）。 “分类”是对类别的预测（例如，低，中或高最大未来涡度）。

在二元分类中，有两个类别。因此，预测采取回答 是或否问题 的形式。除了将其二值化外，我们将使用相同的目标变量（最大未来涡度）。问题将是预测最大未来涡度是否超过阈值。

二值化

下一个单元格将目标变量“二值化”（将每个值转换为 0 或 1，是或否）。

阈值是所有训练示例中最大未来涡度的 90％。

使用相同的阈值对训练，验证和测试数据进行二值化。

使用的函数

get_binarization_threshold 用于计算阈值。

def get_binarization_threshold(
    csv_file_names, 
    percentile_level: float,
) -> float:
    max_target_values = np.array([])
    
    for i in tqdm(range(len(csv_file_names))):
        this_file_name = csv_file_names[i]
        # print(f'Reading data from: "{this_file_name}"...')
        this_target_table = read_feature_file(this_file_name)[-1]

        max_target_values = np.concatenate((
            max_target_values, 
            this_target_table[TARGET_NAME].values
        ))

    binarization_threshold = np.percentile(
        max_target_values, 
        percentile_level
    )

    print(f'\nBinarization threshold for "{TARGET_NAME}" = {binarization_threshold:.4e}')

    return binarization_threshold

示例

get_binarization_threshold(
    csv_file_names=training_file_names, 
    percentile_level=90.
)

Binarization threshold for "RVORT1_MAX-future_max" = 3.8500e-03
0.00385

binarize_target_values 函数将目标值二值化，返回包含 0 或 1 的数组

def binarize_target_values(
    target_values, 
    binarization_threshold
):
    return (target_values >= binarization_threshold).astype(int)

二值化

计算阈值

binarization_threshold = get_binarization_threshold(
    csv_file_names=training_file_names, 
    percentile_level=90.
)

Binarization threshold for "RVORT1_MAX-future_max" = 3.8500e-03

变换训练数据

training_target_values = binarize_target_values(
    target_values=training_target_table[TARGET_NAME].values,
    binarization_threshold=binarization_threshold,
)

BINARIZED_TARGET_NAME = 'strong_future_rotation_flag'

training_target_table = training_target_table.assign(
    **{
        BINARIZED_TARGET_NAME: training_target_values
    }
)

training_target_table[:10]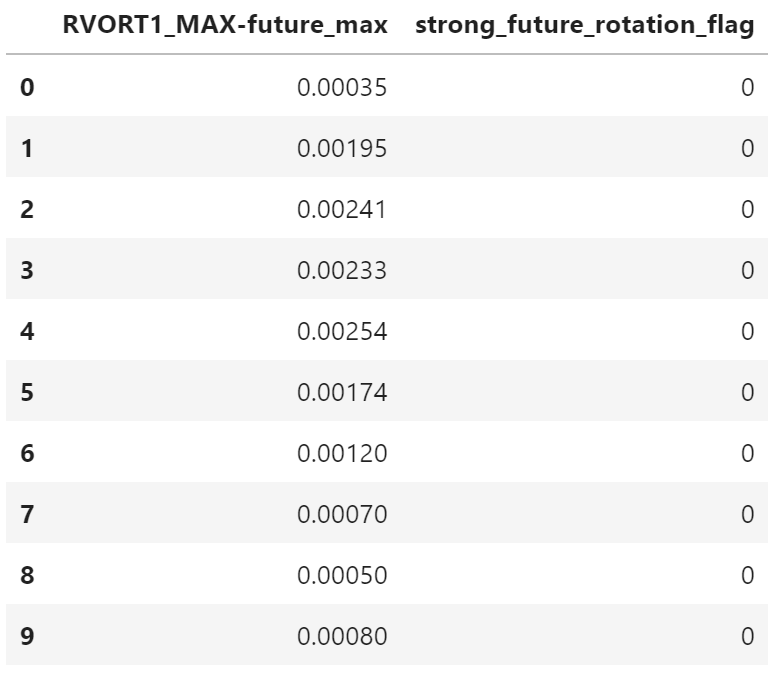

变换验证数据

validation_target_values = binarize_target_values(
    target_values=validation_target_table[TARGET_NAME].values,
    binarization_threshold=binarization_threshold
)

validation_target_table = validation_target_table.assign(
    **{
        BINARIZED_TARGET_NAME: validation_target_values
    }
)

validation_target_table[:10]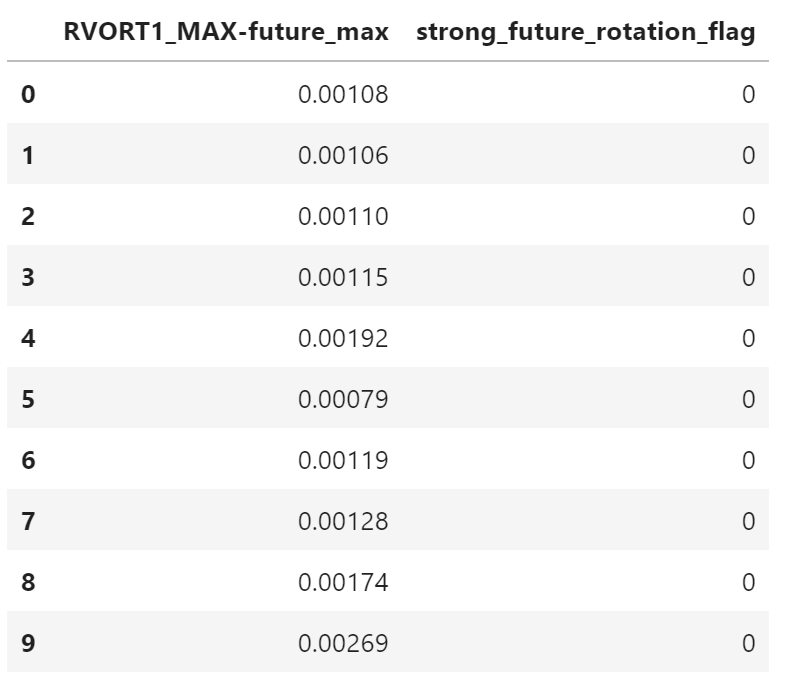

变换测试数据

testing_target_values = binarize_target_values(
    target_values=testing_target_table[TARGET_NAME].values,
    binarization_threshold=binarization_threshold,
)

testing_target_table = testing_target_table.assign(
    **{
        BINARIZED_TARGET_NAME: testing_target_values
    }
)

testing_target_table[:10]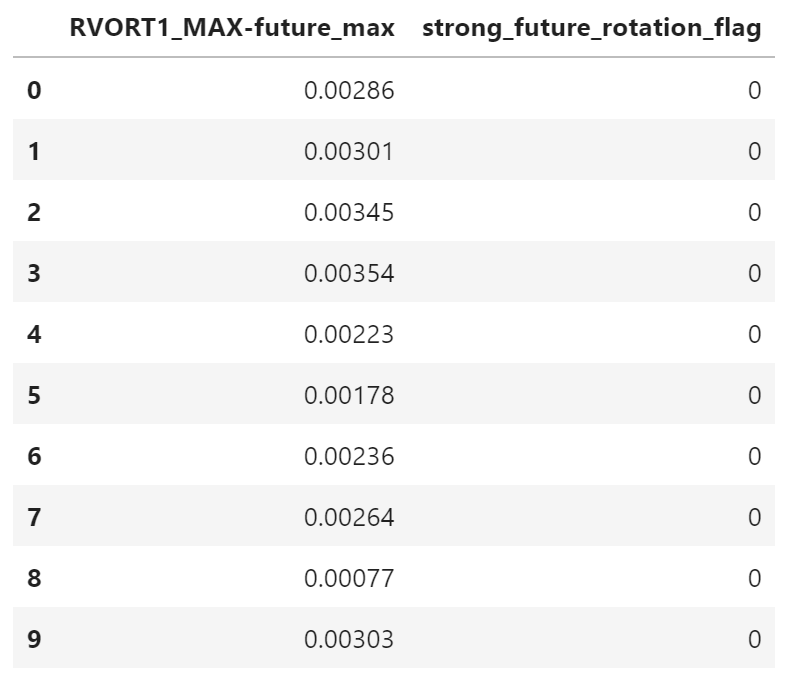

二值化：练习

如果要使用其他百分位数（而不是第 90 位）进行二值化，请在此处随意进行。例如，如果要处理非稀有事件，则可以使用第 50 个百分位数。如果您想处理更罕见的事件，则可以使用第 99 个百分位。

逻辑回归

逻辑回归（Logistic Regression）是用于二分类的基本线性回归方法。

回顾线性回归的等式：

\begin{equation*} \hat{y} = \beta_0 + \sum\limits_{j = 1}^{M} \beta_j x_j \end{equation*}

逻辑回归仅改变等式左边：

\begin{equation*} \textrm{ln}(\frac{\hat{y}}{1 - \hat{y}}) = \beta_0 + \sum\limits_{j = 1}^{M} \beta_j x_j \end{equation*}

可以重写为：

\begin{equation*} \hat{y} = \frac{\textrm{exp}(\beta_0 + \sum\limits_{j = 1}^{M} \beta_j x_j)}{1 + \textrm{exp}(\beta_0 + \sum\limits_{j = 1}^{M} \beta_j x_j)} \end{equation*}

上述等式中的 hat{y} 被限制为 [0, 1]，因此可以将其解释为概率。权重（beta_0 和 beta_j）以最小化交叉熵训练，而不是均方误差。

\begin{equation*} \epsilon = -\frac{1}{N} \sum\limits_{i = 1}^{N} \left[ y_i\textrm{ log}_2(\hat{y}_i) + (1 - y_i)\textrm{ log}_2(1 - \hat{y}_i) \right] \end{equation*}

hat{y}_{i} 是第 i 个样本的预报概率。这是事件发生的概率（因此类别 = 1 或“是”）。在我们的案例中，这是最大未来涡度 >= 3.850×10^−3 s^−1的概率

y_{i} 是第 1 个样本的标签（0 或 1）

N 是训练样本的个数

epsilon 是交叉熵

交叉熵的范围是 [0, ∞)，并且是负向的（越低越好）

交叉熵来自信息论，与描述两种分布（预测和标签）之间的差异所需的位数成正比。

当分布相等时（对于所有正例，hat{y}_{i} = 1.0，对于所有负例，hat{y}_{i} = 0.0），位数为零，因此交叉熵为零。

对于线性回归，关于交叉熵的模型系数的导数如下：

\begin{equation*} \frac{\partial \epsilon}{\partial \beta_0} = \frac{2}{N} \sum\limits_{i = 1}^{N} (\hat{y}_i - y_i) \end{equation*}

\begin{equation*} \frac{\partial \epsilon}{\partial \beta_j} = \frac{2}{N} \sum\limits_{i = 1}^{N} x_{ij} (\hat{y}_i - y_i) \end{equation*}

对于线性回归，权重（beta_{0} 和 beta_{j}）在训练过程中通过梯度下降进行调整。

\begin{equation*} \beta_0 \leftarrow \beta_0 - \alpha \frac{\partial \epsilon}{\partial \beta_0} \end{equation*}

\begin{equation*} \beta_j \leftarrow \beta_j - \alpha \frac{\partial \epsilon}{\partial \beta_j} \end{equation*}

逻辑回归：练习

本文及后续文章将执行以下操作：

训练逻辑回归模型（具有默认的超参数）来预测每场风暴的标签（未来最大涡度是否 >= 3.850×10^−3 s-1）。
在训练和验证数据上评估模型。

对于训练和验证数据，此单元格绘制以下图形：

ROC（receiver operating characteristic）曲线（Metz 1978）
性能图（Performance diagram，Roebber 2009）
属性图（Attributes diagram，Hsu and Murphy 1986）

这些图形在后面的文章中介绍。

创建和训练

创建模型

setup_logistic_regression 用于创建逻辑回归模型，返回随机梯度下降分类器（sklearn.linear_model.SGDClassifier），其中损失函数为 loss='log'

不使用正则化：penalty='none'
仅使用 L2 正则化：penalty='l2'
仅使用 L1 正则化：penalty='l1'
同时使用 L1 和 L2 正则化：penalty='elasticnet'

RANDOM_SEED = 6695
LAMBDA_TOLERANCE = 1e-10

def setup_logistic_regression(
    lambda1: float=0., 
    lambda2: float=0.
):
    assert lambda1 >= 0
    assert lambda2 >= 0
    
    if lambda1 < LAMBDA_TOLERANCE and lambda2 < LAMBDA_TOLERANCE:
        # 不使用正则化
        return sklearn.linear_model.SGDClassifier(
            loss='log', 
            penalty='none', 
            fit_intercept=True, 
            verbose=0,
            random_state=RANDOM_SEED
        )

    if lambda1 < LAMBDA_TOLERANCE:
        # 仅使用 L2 正则化
        return sklearn.linear_model.SGDClassifier(
            loss='log', 
            penalty='l2', 
            alpha=lambda2, 
            fit_intercept=True,
            verbose=0, 
            random_state=RANDOM_SEED
        )

    if lambda2 < LAMBDA_TOLERANCE:
        # 仅使用 L1 正则化
        return sklearn.linear_model.SGDClassifier(
            loss='log', 
            penalty='l1', 
            alpha=lambda1, 
            fit_intercept=True,
            verbose=0, 
            random_state=RANDOM_SEED
        )

    alpha, l1_ratio = _lambdas_to_sklearn_inputs(
        lambda1=lambda1, 
        lambda2=lambda2
    )
    # 同时使用 L1 和 L2 正则化
    return sklearn.linear_model.SGDClassifier(
        loss='log', 
        penalty='elasticnet', 
        alpha=alpha, 
        l1_ratio=l1_ratio,
        fit_intercept=True, 
        verbose=0, 
        random_state=RANDOM_SEED
    )

_lambdas_to_sklearn_inputs 函数生成 ElasticNet 需要的参数

def _lambdas_to_sklearn_inputs(lambda1, lambda2):
    return lambda1 + lambda2, lambda1 / (lambda1 + lambda2)

训练模型

train_logistic_regression 函数用于训练逻辑回归模型

注：scikit-learn 所有模型类都有相同的 API 接口

def train_logistic_regression(
    model, 
    training_predictor_table: pd.DataFrame,
    training_target_table: pd.DataFrame,
):
    model.fit(
        X=training_predictor_table.values,
        y=training_target_table[BINARIZED_TARGET_NAME].values
    )

    return model

使用实际数据

训练模型

plain_log_model = setup_logistic_regression(
    lambda1=0.,
    lambda2=0.,
)
plain_log_model

SGDClassifier(loss='log', penalty='none', random_state=6695)

_ = train_logistic_regression(
    model=plain_log_model,
    training_predictor_table=training_predictor_table,
    training_target_table=training_target_table,
)

training_probabilities = plain_log_model.predict_proba(
    training_predictor_table.values
)[:, 1]
training_probabilities

array([0.0086618 , 0.04224638, 0.035335  , ..., 0.01315788, 0.00710323,
       0.00226968])

training_event_frequency = np.mean(
    training_target_table["strong_future_rotation_flag"].values
)
training_event_frequency

0.10034434450161697

评估性能

后续文章将介绍三种用于评估性能的图形。

参考

https://github.com/djgagne/ams-ml-python-course

AMS 机器学习课程

数据预处理：

《AMS机器学习课程：数据分析与预处理》

实际数据处理：

《AMS机器学习课程：预测雷暴旋转的基础机器学习 - 数据》

线性回归：

《AMS机器学习课程：预测雷暴旋转的基础机器学习 - 线性回归》

《AMS机器学习课程：预测雷暴旋转的基础机器学习 - 正则化》

《AMS机器学习课程：预测雷暴旋转的基础机器学习 - 超参数试验》