AMS机器学习课程：预测雷暴旋转的基础机器学习 - 超参数试验

August 08, 2020 (最后修改: August 22, 2021)

本文翻译自 AMS 机器学习 Python 教程，并有部分修改。
Lagerquist, R., and D.J. Gagne II, 2019: “Basic machine learning for predicting thunderstorm rotation: Python tutorial”. https://github.com/djgagne/ams-ml-python-course/blob/master/module_2/ML_Short_Course_Module_2_Basic.ipynb.

本文接上一篇文章

《AMS机器学习课程：预测雷暴旋转的基础机器学习 - 正则化》

L1 和 L2 正则化的超参数试验

接下来的几个单元格将向您展示如何进行“超参数实验”。 超参数实验的步骤如下。

选择要尝试的值。 这通常基于对模型如何工作的一些先验知识。您拥有的专业知识越多，可以尝试的值范围就越窄。在这种情况下，我们尝试

\begin{equation*} \lambda_1 \in \lbrace 10^{-8}, 10^{-7.5}, 10^{-7}, 10^{-6.5}, 10^{-6}, 10^{-5.5}, 10^{-5}, 10^{-4.5}, 10^{-4} \rbrace \end{equation*}

和

\begin{equation*} \lambda_2 \in \lbrace 10^{-4}, 10^{-3.5}, 10^{-3}, 10^{-2.5}, 10^{-2}, 10^{-1.5}, 10^{-1}, 10^{-0.5}, 10^{0}, 10^{0.5}, 10^{1} \rbrace \end{equation*}

使用每种超参数组合训练模型。 在这种情况下，lambda_{1} 有9个值，lambda_{2} 有 11 个值，因此有 99 个组合。这称为“网格搜索（grid search）”。（注意：除了网格搜索，还有其他搜索方法。这些方法特别有用，特别是当组合的数量太大（“组合爆炸”）时，如果您尝试的是几个以上的超参数，通常会发生这种情况。在这种情况下，您可以进行 random search 或 beam search，使用遗传算法来进化超参数，等等。但是在此模块中，我们将坚持使用网格搜索。）
根据验证数据评估每个模型
查找在验证数据上表现最佳的模型。 同样，有很多方法可以定义“最佳”。在这里，我们将选择 MAE 技能得分最高的模型。

超参数试验：训练

下一个单元格执行超参数实验的步骤 1 和 2（定义要尝试的值并训练模型）。

下面的代码会使用不同的参数组合训练 ElasticNet 回归模型，并将模型的评估结果保存到数组中。

lambda1_values = np.logspace(-8, -4, num=9)
lambda2_values = np.logspace(-4, 1, num=11)

num_lambda1 = len(lambda1_values)
num_lambda2 = len(lambda2_values)

validation_mae_matrix_s01 = np.full(
    (num_lambda1, num_lambda2),
    np.nan,
)

validation_mse_matrix_s02 = np.full(
    (num_lambda1, num_lambda2),
    np.nan
)

validation_mae_skill_matrix = np.full(
    (num_lambda1, num_lambda2),
    np.nan
)

validation_mse_skill_matrix = np.full(
    (num_lambda1, num_lambda2),
    np.nan
)

mean_training_target_value = np.mean(
    training_target_table[TARGET_NAME].values
)

from tqdm.notebook import tnrange, tqdm_notebook


for i in tqdm_notebook(range(num_lambda1)):
    for j in tqdm_notebook(range(num_lambda2), leave=False):      
        model = setup_linear_regression(
            lambda1=lambda1_values[i],
            lambda2=lambda2_values[j],
        )
        
        _ = train_linear_regression(
            model=model,
            training_predictor_table=training_predictor_table,
            training_target_table=training_target_table
        )

        validation_predictions = model.predict(
            validation_predictor_table.values
        )

        evaluation_dict = evaluate_regression(
            target_values=validation_target_table[TARGET_NAME].values,
            predicted_target_values=validation_predictions,
            mean_training_target_value=mean_training_target_value,
            verbose=False, 
            create_plots=False
        )
        
        validation_mae_matrix_s01[i, j] = evaluation_dict[MAE_KEY]
        validation_mse_matrix_s02[i, j] = evaluation_dict[MSE_KEY]
        validation_mae_skill_matrix[i, j] = evaluation_dict[MAE_SKILL_SCORE_KEY]
        validation_mse_skill_matrix[i, j] = evaluation_dict[MSE_SKILL_SCORE_KEY]

验证

下一个单元格执行超参数实验的步骤 3（在验证数据上评估每个模型）。

使用到的函数

plot_scores_2d 函数绘制二维网格评分图

import matplotlib.colors

def plot_scores_2d(
    score_matrix: np.ndarray, 
    min_colour_value: float, 
    max_colour_value: float, 
    x_tick_labels: np.ndarray,
    y_tick_labels: np.ndarray, 
    colour_map_object=pyplot.cm.plasma
):
    _, axes_object = pyplot.subplots(
        1, 1, 
        figsize=(10, 10)
    )
    
    # 绘制网格图
    pyplot.imshow(
        score_matrix, 
        cmap=colour_map_object, 
        origin='lower',
        vmin=min_colour_value, 
        vmax=max_colour_value
    )

    x_tick_values = np.linspace(
        0, score_matrix.shape[1] - 1, 
        num=score_matrix.shape[1],
        dtype=float
    )
    y_tick_values = np.linspace(
        0, score_matrix.shape[0] - 1, 
        num=score_matrix.shape[0], 
        dtype=float
    )

    pyplot.xticks(x_tick_values, x_tick_labels)
    pyplot.yticks(y_tick_values, y_tick_labels)
    
    # 绘制颜色条
    _add_colour_bar(
        axes_object=axes_object, 
        colour_map_object=colour_map_object,
        values_to_colour=score_matrix, 
        min_colour_value=min_colour_value,
        max_colour_value=max_colour_value
    )

_add_colour_bar 函数向已有的图形中添加颜色条，返回创建的颜色条

def _add_colour_bar(
    axes_object, 
    colour_map_object: matplotlib.pyplot.cm, 
    values_to_colour: np.ndarray, 
    min_colour_value: float,
    max_colour_value: float, 
    colour_norm_object=None,
    orientation_string='vertical',
    extend_min=True, 
    extend_max=True
) -> matplotlib.pyplot.colorbar:
    if colour_norm_object is None:
        # 归一化函数
        colour_norm_object = matplotlib.colors.Normalize(
            vmin=min_colour_value, 
            vmax=max_colour_value, 
            clip=False
        )
    
    # 将标量值映射到 RGBA
    scalar_mappable_object = pyplot.cm.ScalarMappable(
        cmap=colour_map_object, 
        norm=colour_norm_object
    )
    scalar_mappable_object.set_array(values_to_colour)

    if extend_min and extend_max:
        extend_string = 'both'
    elif extend_min:
        extend_string = 'min'
    elif extend_max:
        extend_string = 'max'
    else:
        extend_string = 'neither'

    if orientation_string == 'horizontal':
        padding = 0.075
    else:
        padding = 0.05

    colour_bar_object = pyplot.colorbar(
        ax=axes_object, 
        mappable=scalar_mappable_object,
        orientation=orientation_string, 
        pad=padding, 
        extend=extend_string,
        shrink=0.8
    )

    colour_bar_object.ax.tick_params(labelsize=20)
    return colour_bar_object

验证

MAE

plot_scores_2d(
    score_matrix=validation_mae_matrix_s01,
    min_colour_value=np.percentile(validation_mae_matrix_s01, 1.),
    max_colour_value=np.percentile(validation_mae_matrix_s01, 99.),
    x_tick_labels=np.log10(lambda2_values),
    y_tick_labels=np.log10(lambda1_values)
)

pyplot.xlabel(r'log$_{10}$ of ridge coefficient ($\lambda_2$)')
pyplot.ylabel(r'log$_{10}$ of lasso coefficient ($\lambda_1$)')
pyplot.title(r'Mean absolute error (s$^{-1}$) on validation data')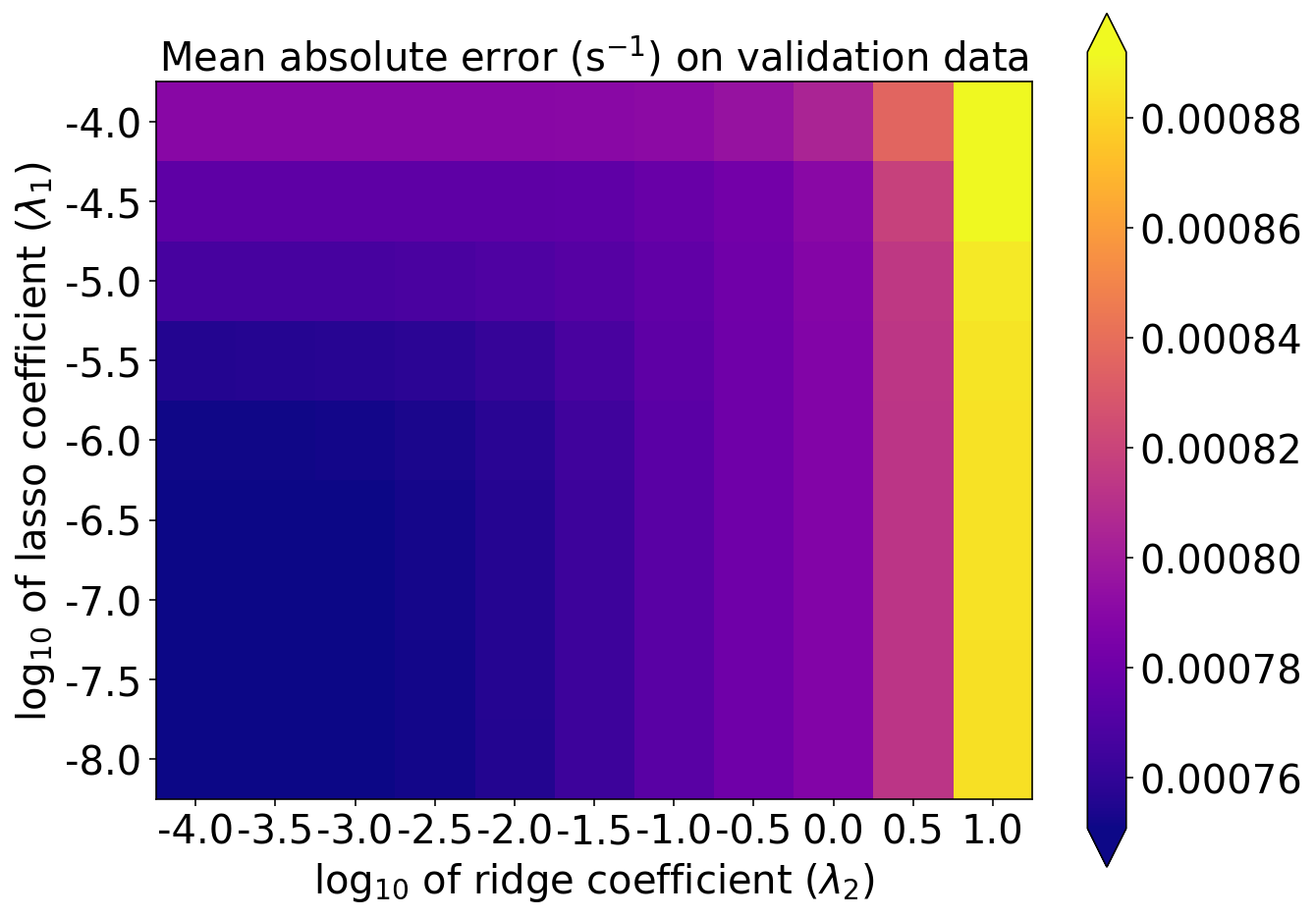

MSE

plot_scores_2d(
    score_matrix=validation_mse_matrix_s02,
    min_colour_value=np.percentile(validation_mse_matrix_s02, 1.),
    max_colour_value=np.percentile(validation_mse_matrix_s02, 99.),
    x_tick_labels=np.log10(lambda2_values),
    y_tick_labels=np.log10(lambda1_values)
)

pyplot.xlabel(r'log$_{10}$ of ridge coefficient ($\lambda_2$)')
pyplot.ylabel(r'log$_{10}$ of lasso coefficient ($\lambda_1$)')
pyplot.title(r'Mean squared error (s$^{-2}$) on validation data')

MAE 技巧评分

plot_scores_2d(
    score_matrix=validation_mae_skill_matrix,
    min_colour_value=np.percentile(validation_mae_skill_matrix, 1.),
    max_colour_value=np.percentile(validation_mae_skill_matrix, 99.),
    x_tick_labels=np.log10(lambda2_values),
    y_tick_labels=np.log10(lambda1_values)
)

pyplot.xlabel(r'log$_{10}$ of ridge coefficient ($\lambda_2$)')
pyplot.ylabel(r'log$_{10}$ of lasso coefficient ($\lambda_1$)')
pyplot.title(r'MAE skill score on validation data')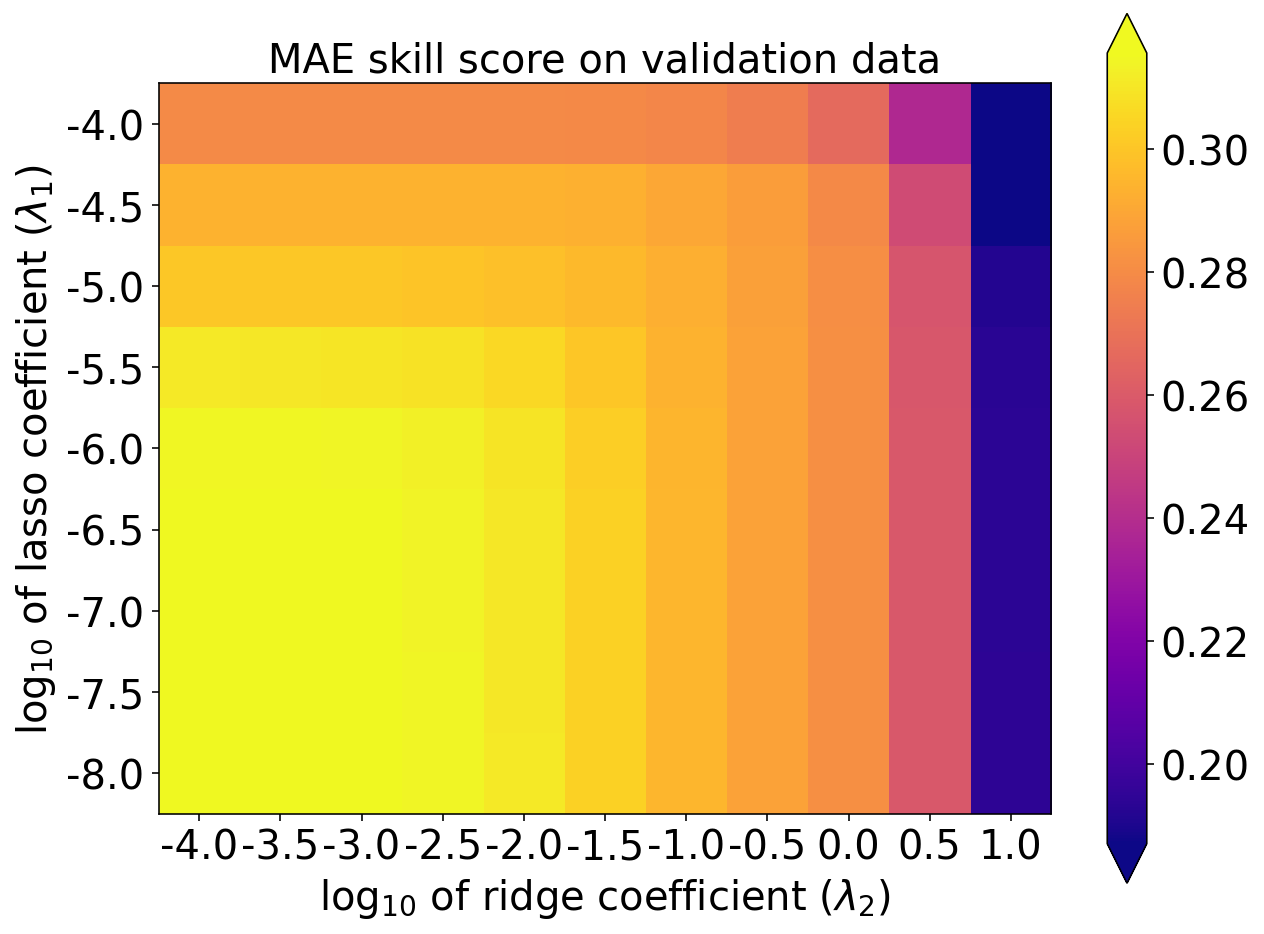

MSE 技巧评分

plot_scores_2d(
    score_matrix=validation_mse_skill_matrix,
    min_colour_value=np.percentile(validation_mse_skill_matrix, 1.),
    max_colour_value=np.percentile(validation_mse_skill_matrix, 99.),
    x_tick_labels=np.log10(lambda2_values),
    y_tick_labels=np.log10(lambda1_values)
)

pyplot.xlabel(r'log$_{10}$ of ridge coefficient ($\lambda_2$)')
pyplot.ylabel(r'log$_{10}$ of lasso coefficient ($\lambda_1$)')
pyplot.title(r'MSE skill score on validation data')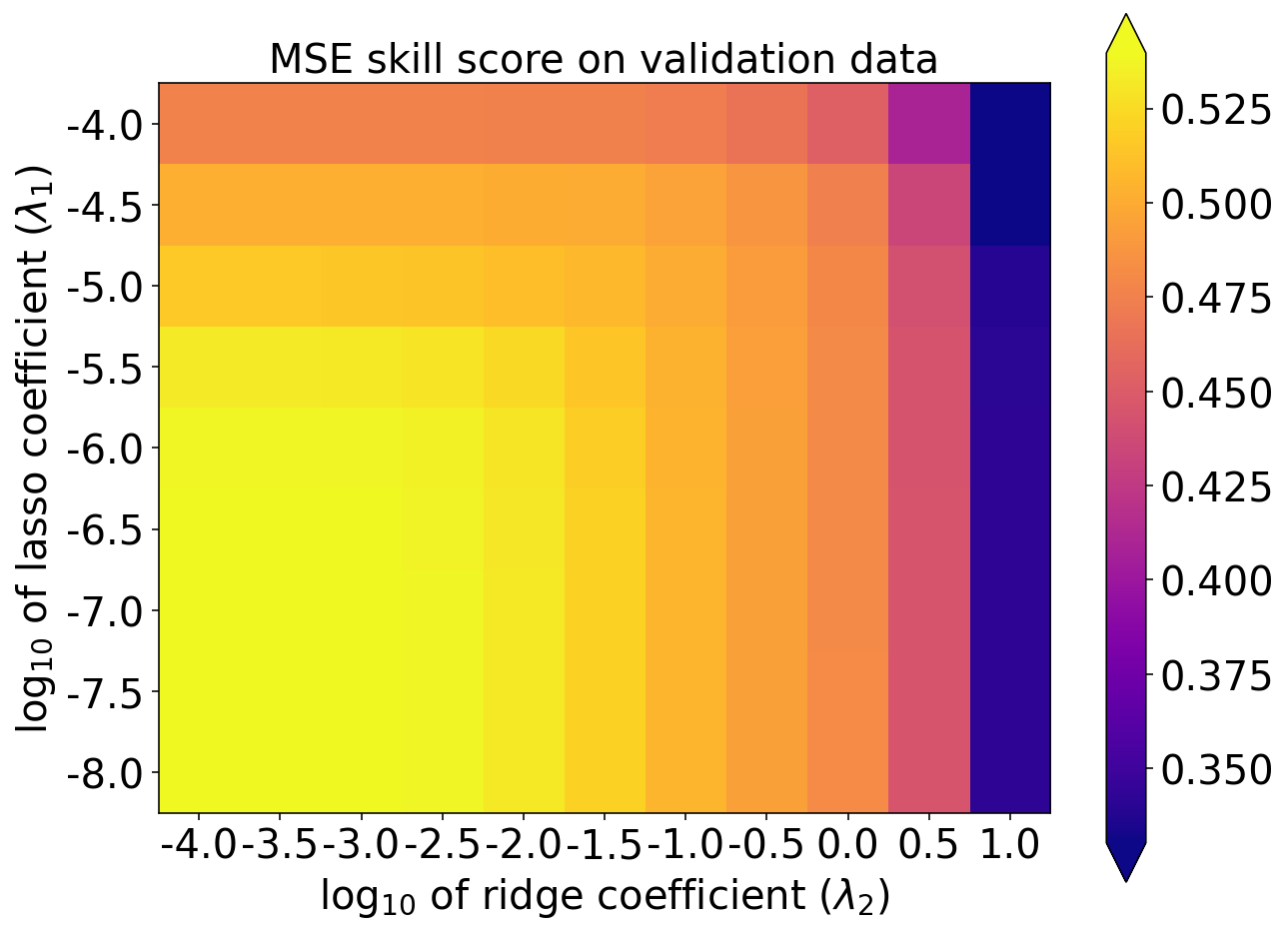

选择

下一个单元格执行超参数实验的第 4 步（选择模型）。

best_linear_index = np.argmax(
    np.ravel(validation_mae_skill_matrix)
)
best_linear_index

注：

np.ravel 将多维数组展开成一维数组

np.argmax 返回最大值的索引

best_lambda1_index, best_lambda2_index = np.unravel_index(
    best_linear_index,
    (len(lambda1_values), len(lambda2_values))
)
best_lambda1_index, best_lambda2_index

(3, 0)

注：

np.unravel_index 将平面索引转换成坐标系统中的坐标

best_lambda1 = lambda1_values[best_lambda1_index]
best_lambda2 = lambda2_values[best_lambda2_index]
best_validation_maess = np.max(validation_mae_skill_matrix)

print(
    f'Best MAE skill score on validation data = {best_validation_maess:.3f} ...\ncorresponding '
    f'lasso coeff = 10^{np.log10(best_lambda1):.1f}, '
    f'ridge coeff = 10^{np.log10(best_lambda2):.1f}'
)

Best MAE skill score on validation data = 0.316 ...
corresponding lasso coeff = 10^-6.5, ridge coeff = 10^-4.0

构造并训练模型

final_model = setup_linear_regression(
    lambda1=best_lambda1,
    lambda2=best_lambda2,
)

_ = train_linear_regression(
    model=final_model,
    training_predictor_table=training_predictor_table,
    training_target_table=training_target_table,
)

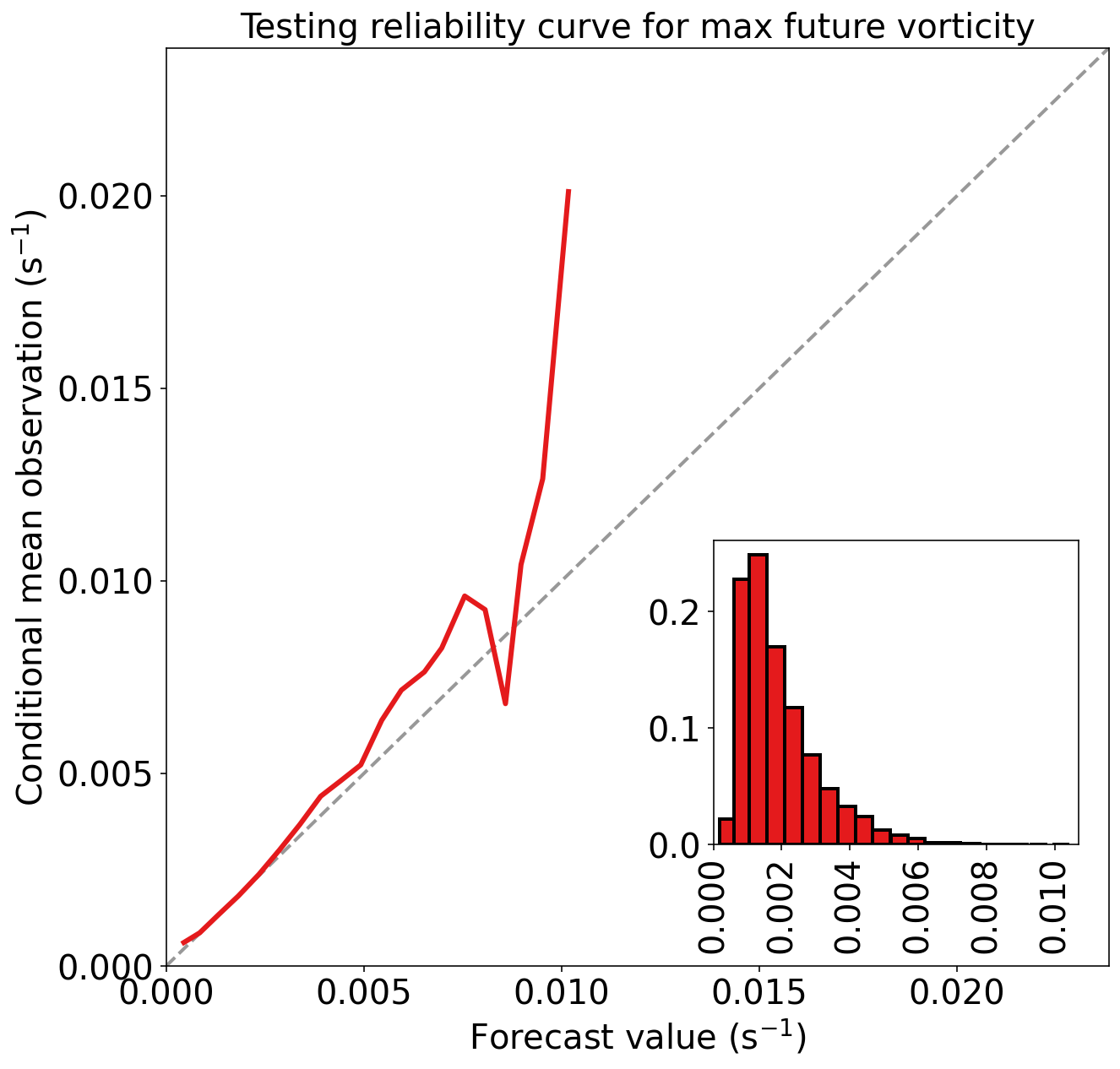
在测试集上的性能

testing_predictions = final_model.predict(
    testing_predictor_table.values
)

mean_training_target_value = np.mean(
    training_target_table[TARGET_NAME].values
)

evaluation_dict = evaluate_regression(
    target_values=testing_target_table[TARGET_NAME].values,
    predicted_target_values=testing_predictions,
    mean_training_target_value=mean_training_target_value,
    dataset_name="testing",
)

Testing MAE (mean absolute error) = 8.257e-04 s^-1
Testing MSE (mean squared error) = 1.413e-06 s^-2
Testing bias (mean signed error) = -8.985e-05 s^-1
Testing MAE skill score (improvement over climatology) = 0.338
Testing MSE skill score (improvement over climatology) = 0.555

练习

基于第一个超参数实验，编写您自己的超参数实验（使用 lambda1 和 lambda2 值的不同集合）。看看是否可以找到在验证数据上更有效的 lambda1-lambda2 组合。如果找到在验证数据上更有效的组合，请查看它在测试数据上是否也更好。如果不是，则 lambda1 和 lambda2在验证数据上过拟合。