AI4ESS 2020：决策树和它们的森林

meteorology/ml
目录

本文翻译自 AI4ESS 2020 课程，并有部分修改

Artificial Intelligence for Earth System Science (AI4ESS) Summer School

Decision Trees and Their Ensembles

Ryan Lagerquist - NOAA

理论

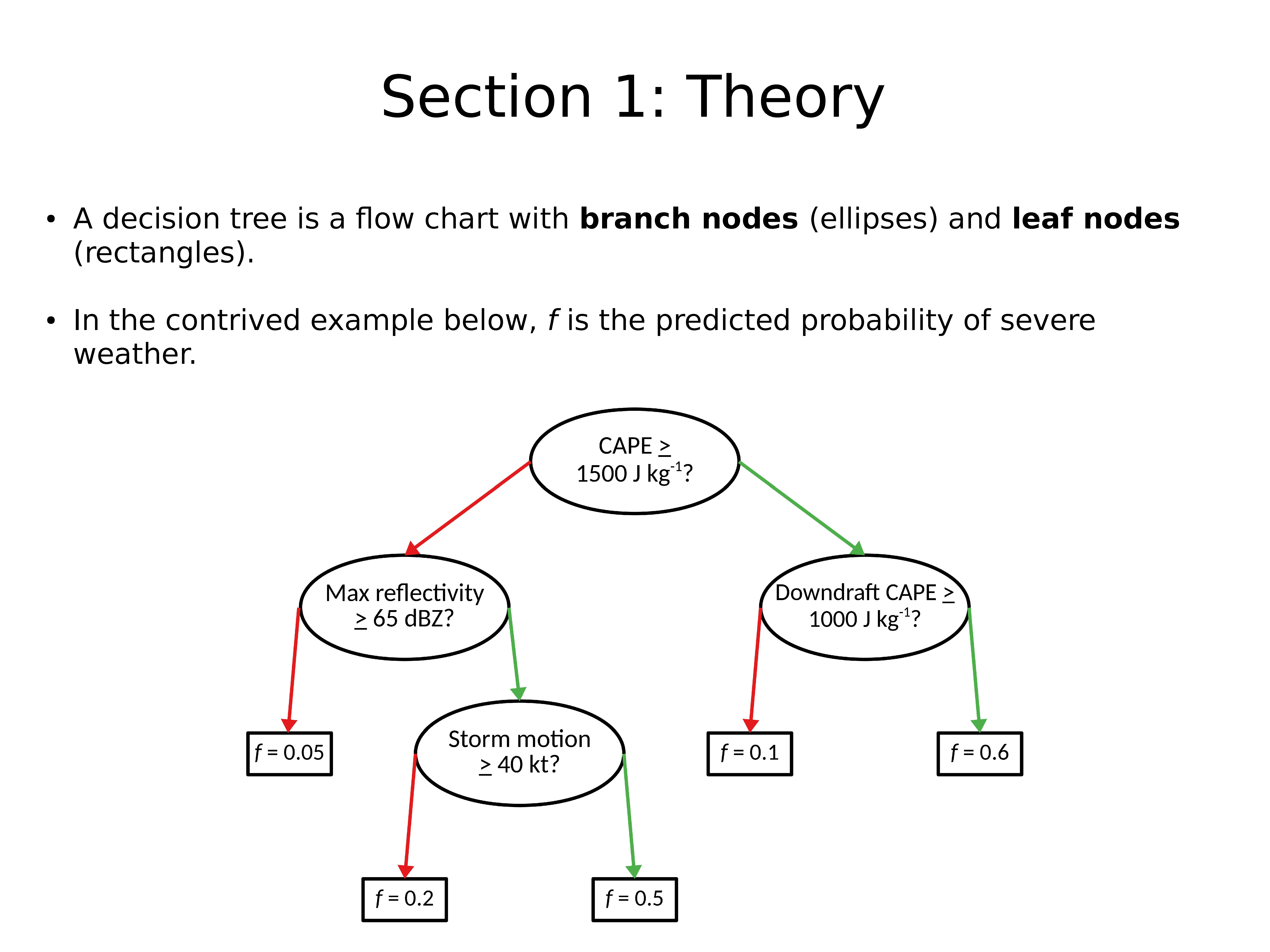
决策树是具有分支节点（椭圆）和叶节点（矩形）的流程图。

在上面的示例中，f 是极端天气的预测概率。

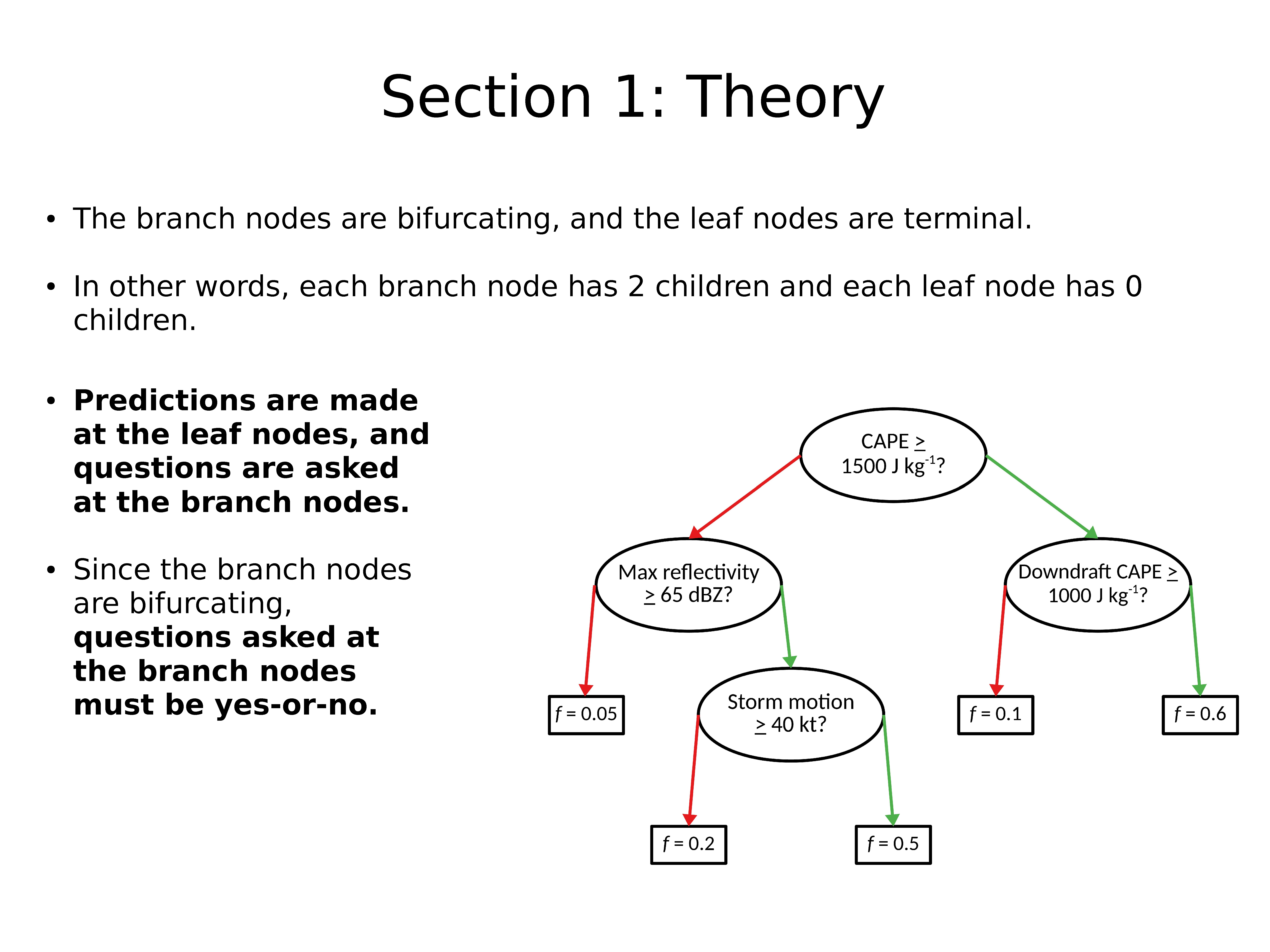
分支节点是分叉的，叶子节点是终止点。

换句话说，每个分支节点有 2 个子节点，每个叶子节点有 0 个子节点。

在叶子节点进行预测，并在分支节点提出问题。

由于分支节点是分支的，因此在分支节点处提出的问题必须为是或否。

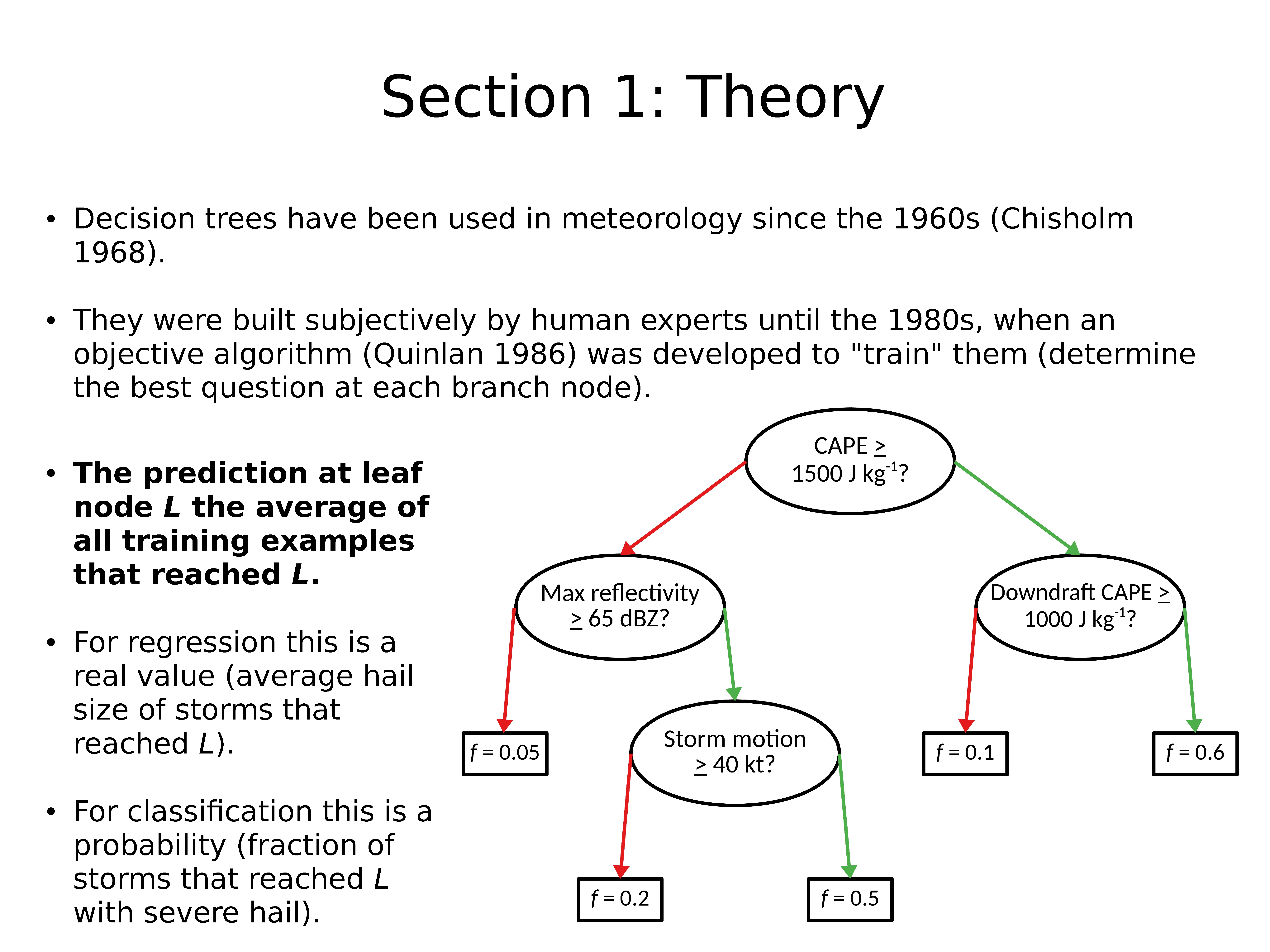
自 1960 年代以来（Chisholm 1968），决策树已用于气象学。

它们由人类专家主观构建，直到 1980 年代，当时开发了一种目标算法（Quinlan 1986）来 “训练” 它们（确定每个分支节点的最佳问题）。

叶节点 L 处的预测是达到 L 的所有训练样本的平均值。

对于回归，这是一个真实值（达到 L 的平均冰雹大小）。

对于分类，这是一个概率（严重冰雹达到 L 的暴风的分数）。

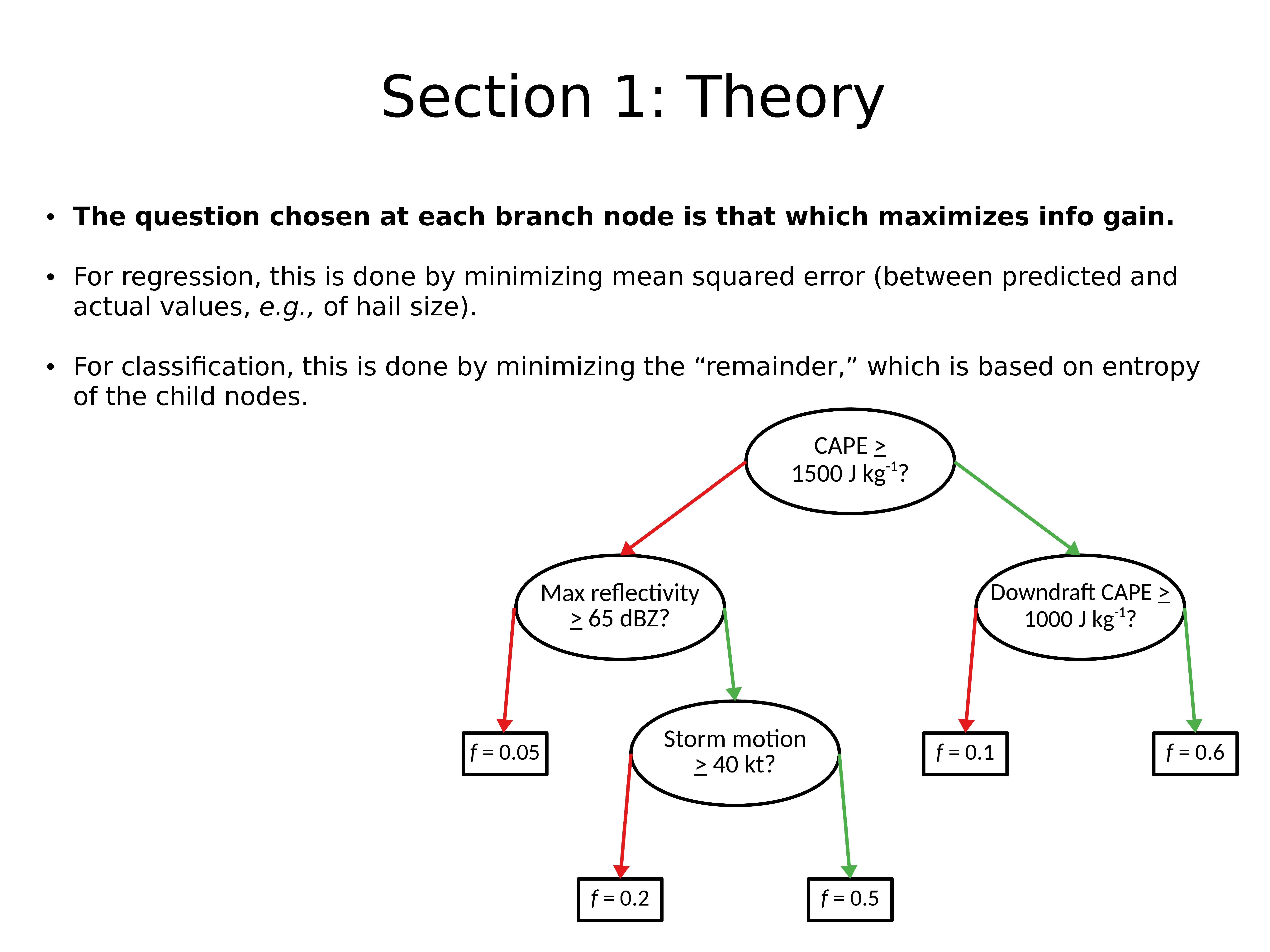
在每个分支节点处选择最大化信息增益的问题。

对于回归，这是通过最小化均方误差来实现的（在预测值和实际值之间，例如冰雹大小）。

对于分类，这是通过最小化 remainder 来完成的，remainder 是基于子节点的熵的。

一个节点的熵定义如下：

\begin{equation*} E=-\frac {1} {n}[\boldsymbol{f}log_{2}(\boldsymbol{f}) + (1-\boldsymbol{f})log_{2}(\boldsymbol{f})] \end{equation*}

其中：

n 是到达该节点的样本个数

f 是这些样本中属于积极类别的分数（例如，严重冰雹而不是非严重冰雹）

那么，remainder 定义如下：

\begin{equation*} \boldsymbol{R} = \frac {n_{left}E_{left} + n_{right}E_{right}} {n_{left}+n_{right}} \end{equation*}

其中：

n_left 是发送给左子节点的样本数（问题的答案为 “否”）

n_left 是发送给右子节点的样本数（问题的答案为 “是”）

E_left 是左子节点的熵

E_right 是右子节点的熵

默认决策树

下面显示的是使用 Python 训练的默认决策树训练数据的结果。

使用默认的输入参数，通过 sklearn.tree.DecisionTreeClassifier 训练树。 （代码）

这棵树被训练用于预测暴风雨将来是否会形成强烈的旋转（涡度 > 0.00385s-1）。

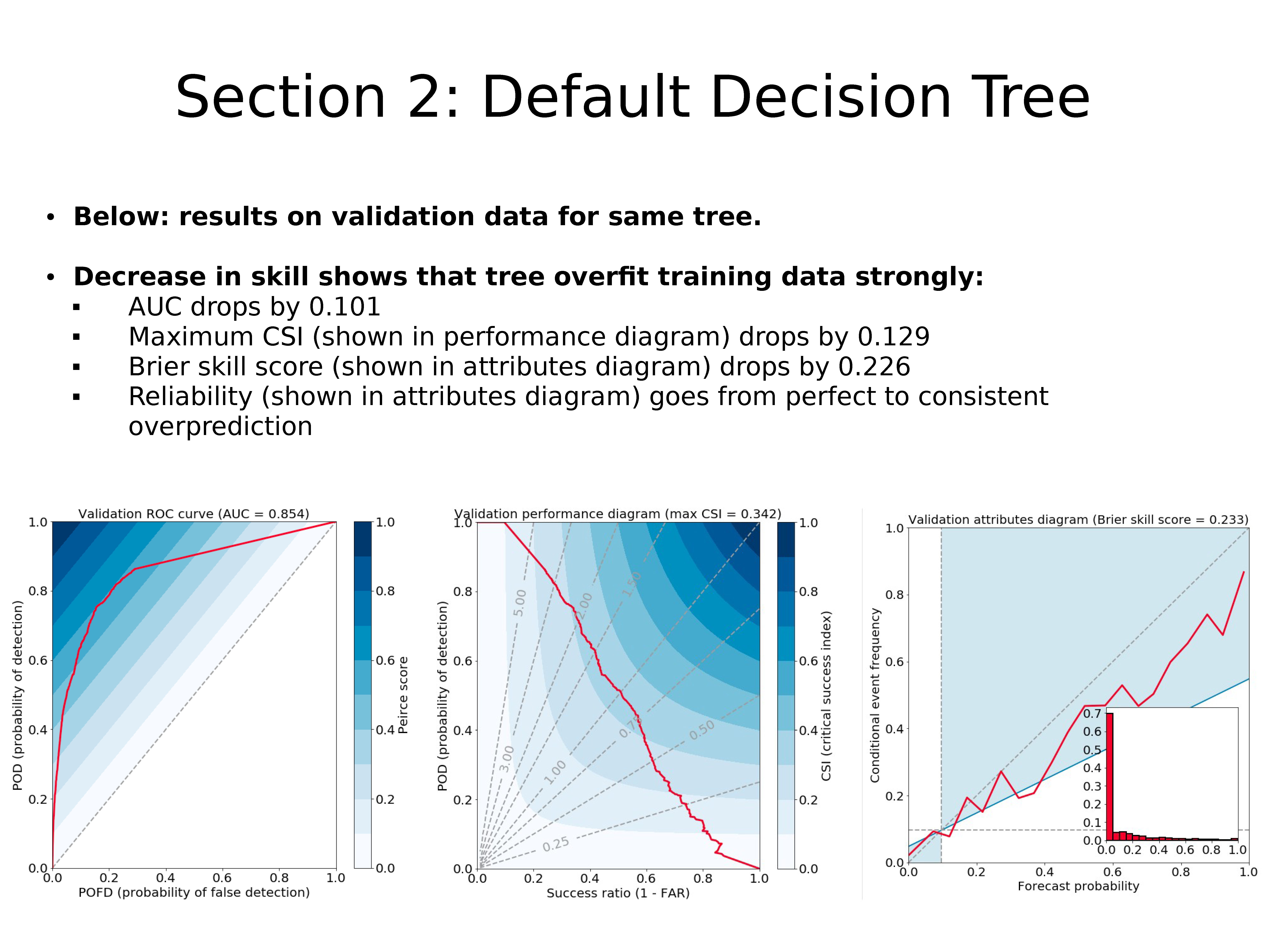
上图：同一棵树在验证数据上的结果。

技巧降低表明该决策树严重过拟合训练数据：

  • AUC 降低 0.101
  • 最大 CSI（如性能图所示）下降 0.129
  • Brier 技巧评分（显示在属性图中）下降了 0.226
  • 可靠性（如属性图所示）从完美变成连续过度预测

更理想的决策树

可以通过限制树的深度来控制过拟合。

两个超参数（以及其他）控制决策树的深度：

  • 分支节点的最小样本数
  • 叶子节点的最小样本数

如果两个值都设置为 1，则树可能会变得很深，从而更容易过拟合

您可以换种方式思考：

  • 如果每个叶节点只有一个示例，则所有预测将仅基于一个训练示例
  • 这些预测可能不会很好地推广到训练数据之外

如果最小样本量太大，则树的深度不够，导致欠拟合

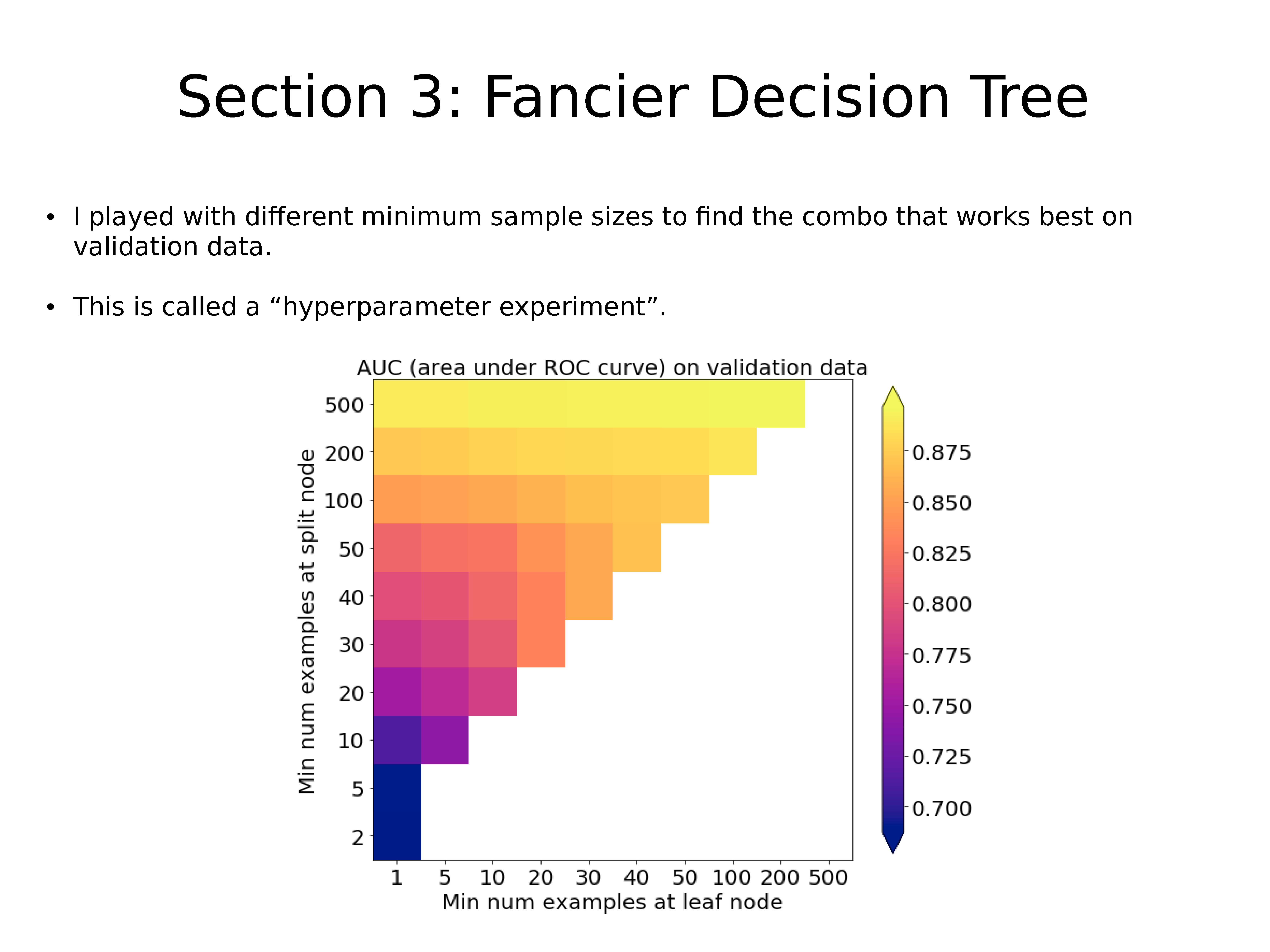
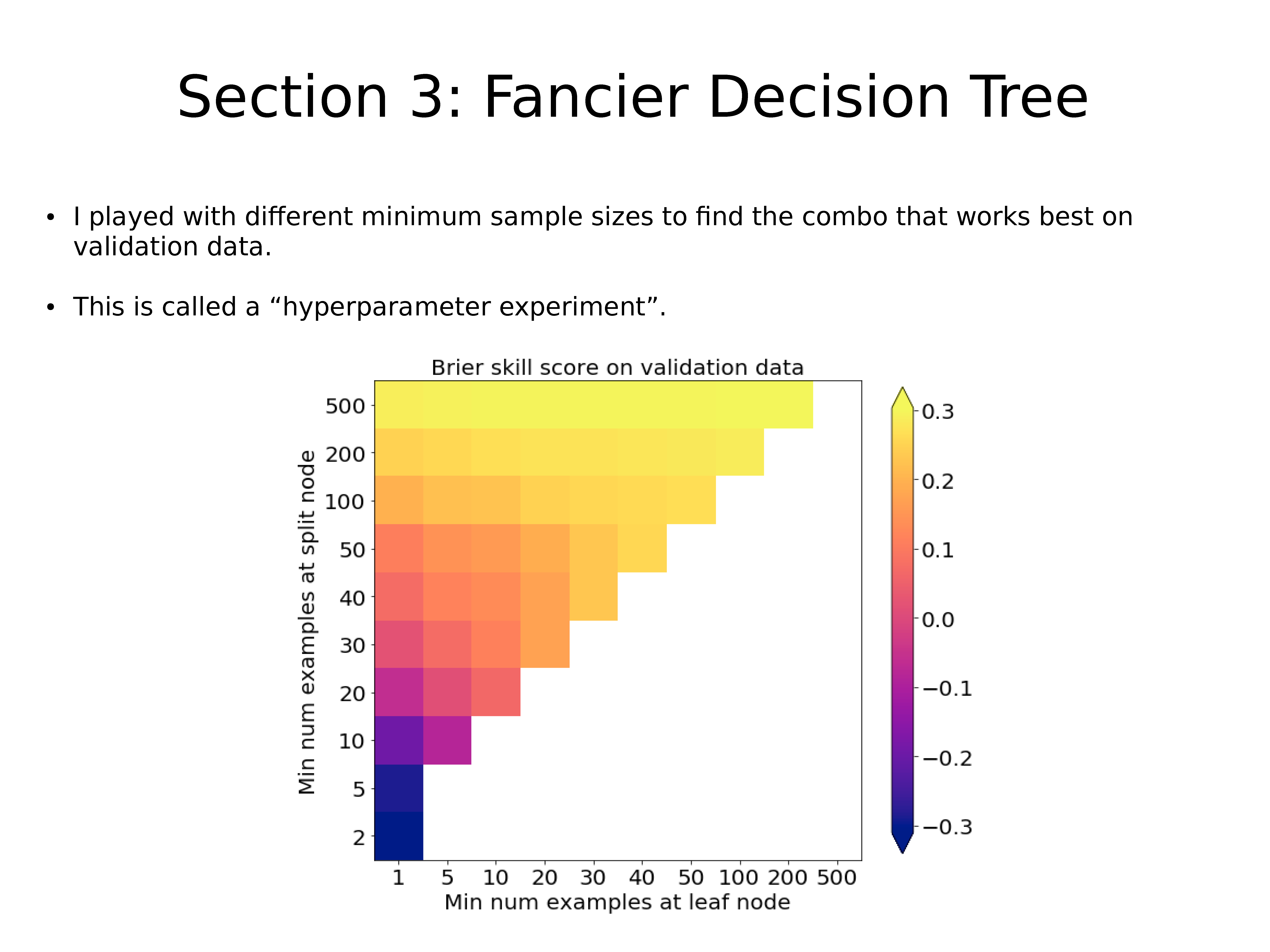
作者使用了不同的最小样本数，以找到最适合验证数据的组合。

这称为 “超参数试验”。

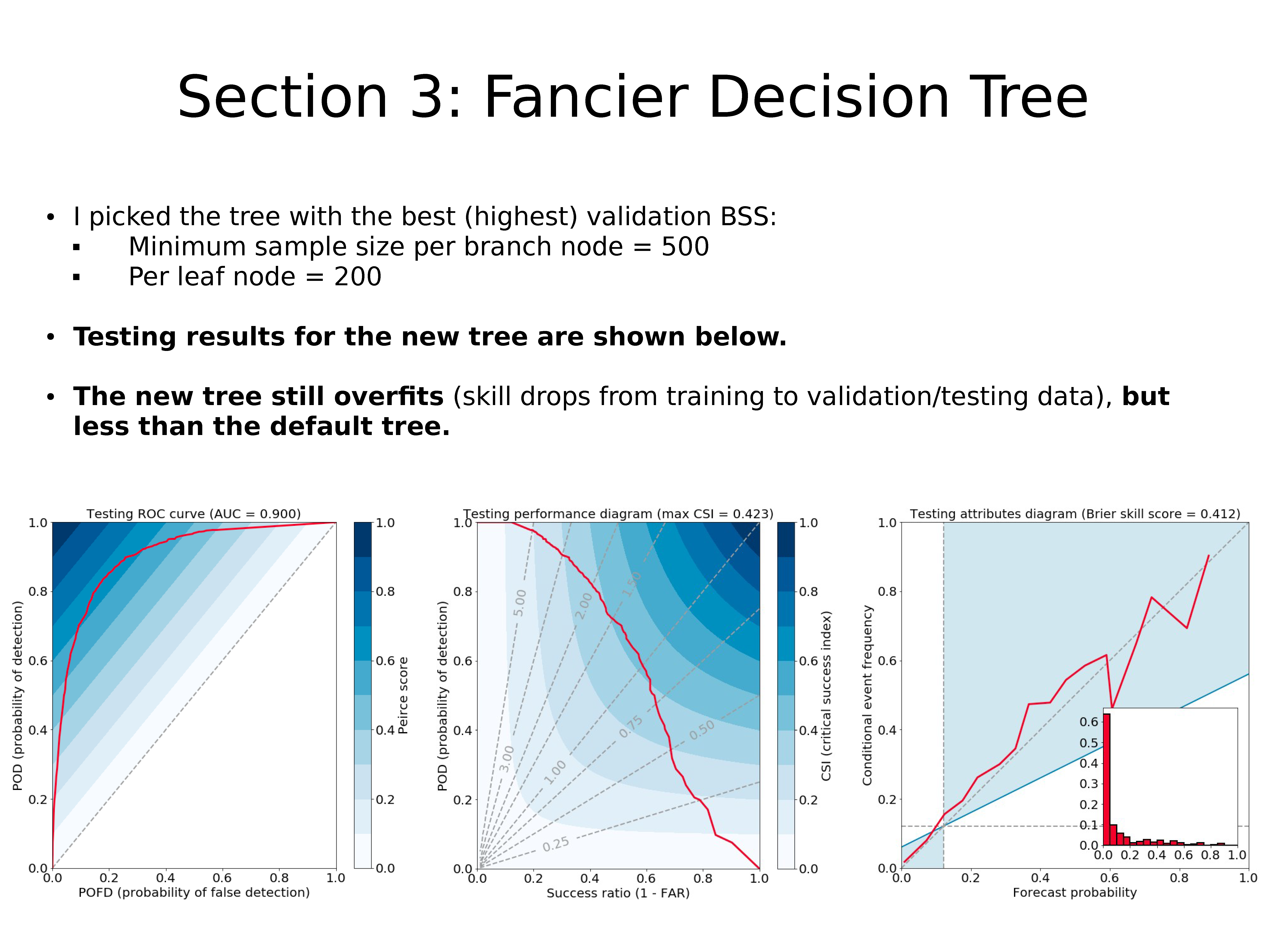
作者选择了具有最佳（最高）验证 BSS 的树：

  • 分支节点最小样本数 = 500
  • 叶子节点样本数 = 200

上图显示了新决策树的测试结果。

新树仍然过拟合（技巧从训练到验证/测试数据有所下降），但少于默认树。

随机森林

随机森林（Breiman 2001）是决策树的集合。

在上一节的单个决策树中，存在很多过拟合问题。

这是决策树的常见问题，因为它们依赖于精确的阈值，这会在决策函数中引入“跳跃”。

例如，在此处显示的树中，CAPE 中的 0.0001 J kg-1 差异可能导致 severe-Wx 概率差异 55％。

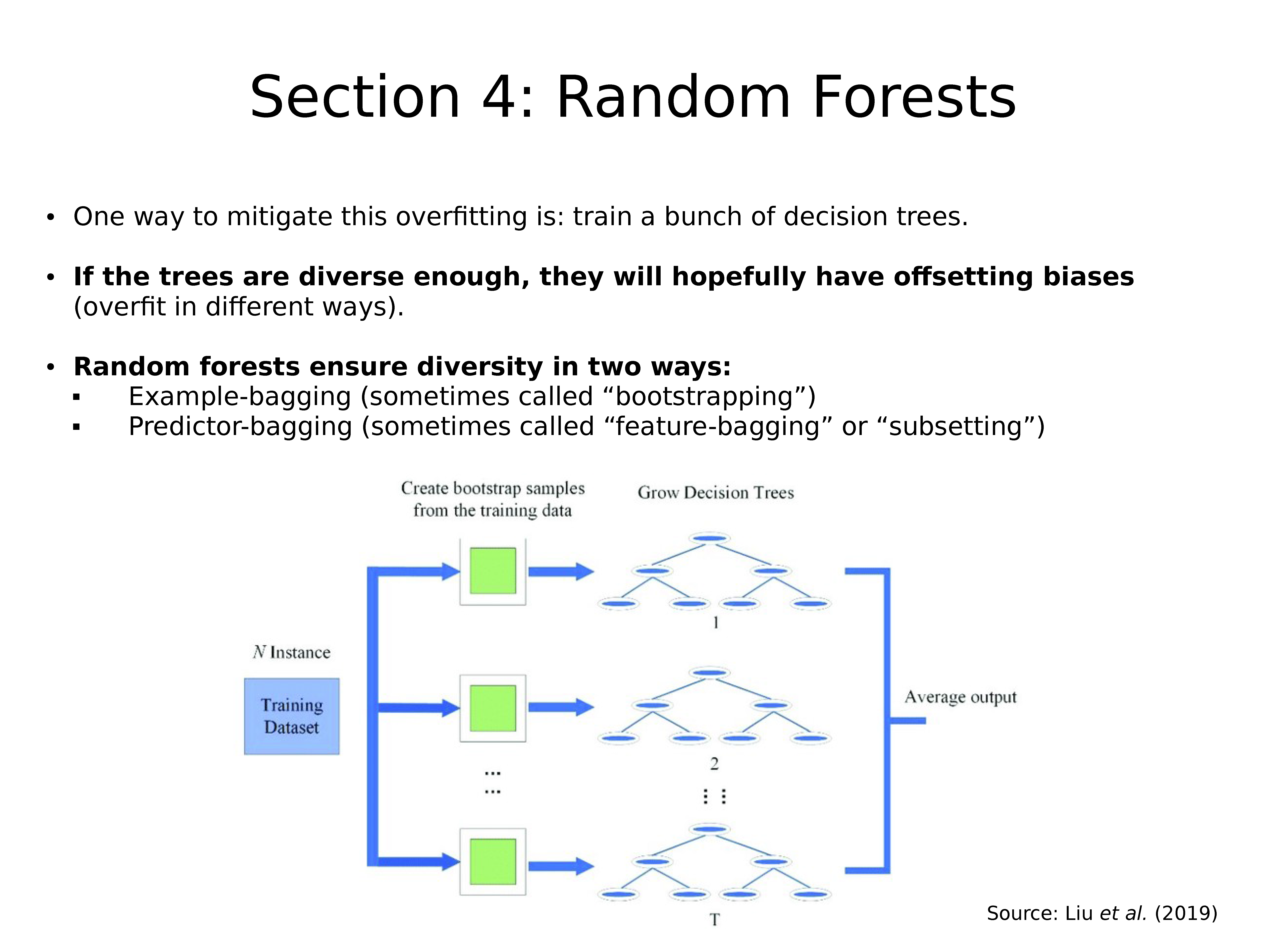
减轻这种过拟合的一种方法是：训练一组决策树

如果树木足够多样化，则希望它们具有抵消的偏差（以不同方式过拟合）。

随机森林通过两种方式确保多样性：

  • Example-bagging (有时被称为 “bootstrapping”)
  • Predictor-bagging (有时被称为 “feature-bagging” or “subsetting”)

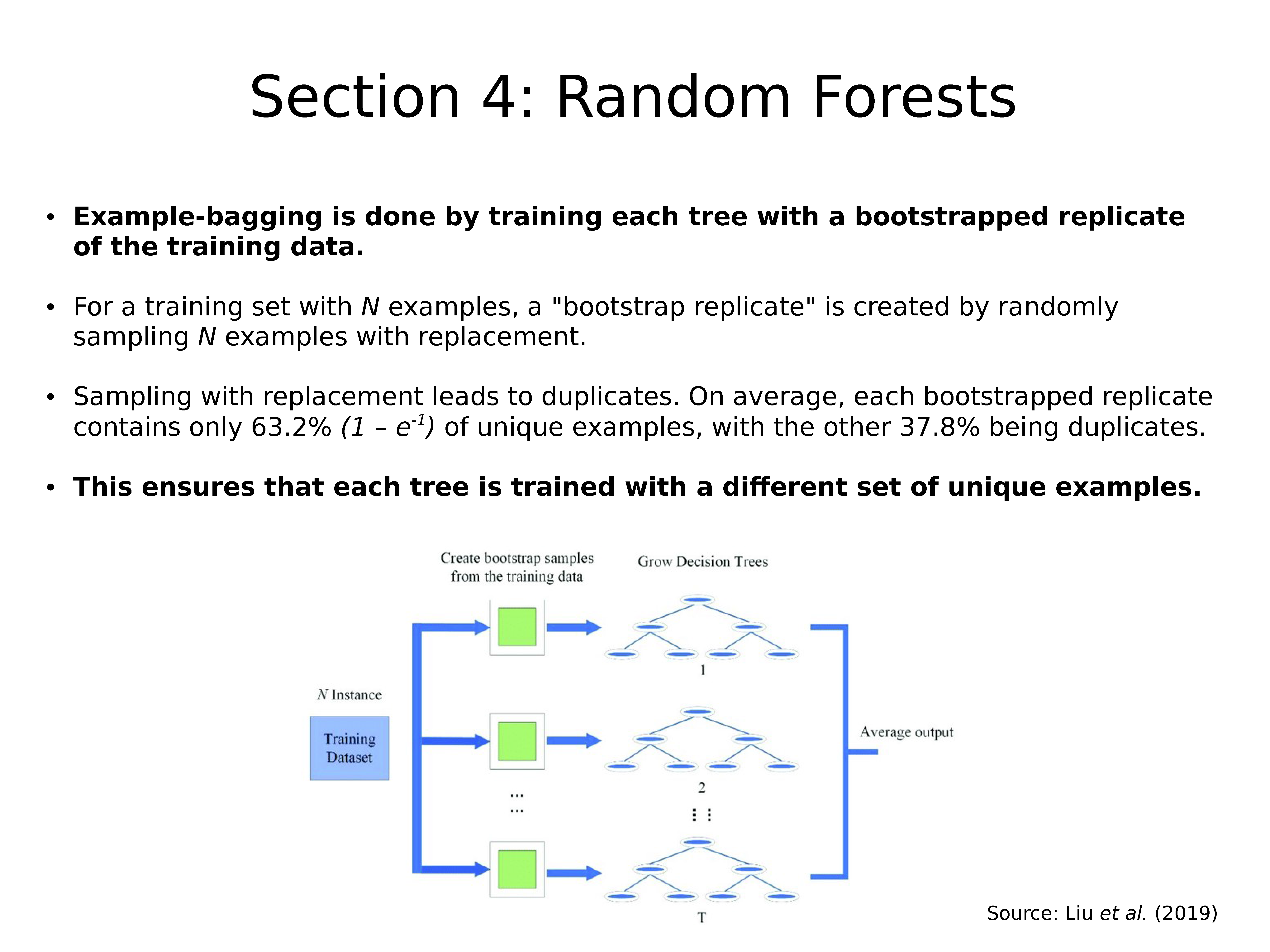
通过使用训练数据的自举副本训练每棵树来完成 Example-bagging。

对于具有 N 个样本的训练集，通过随机采样 N 个可替换的样本来创建 “bootstrap replicate”。

替换采样导致重复。 平均而言，每个引导复制都仅包含63.2％（1 – e^-1）的唯一样本，其他 37.8％ 是重复的。

这样可以确保每棵树都以不同的唯一样本集进行训练。

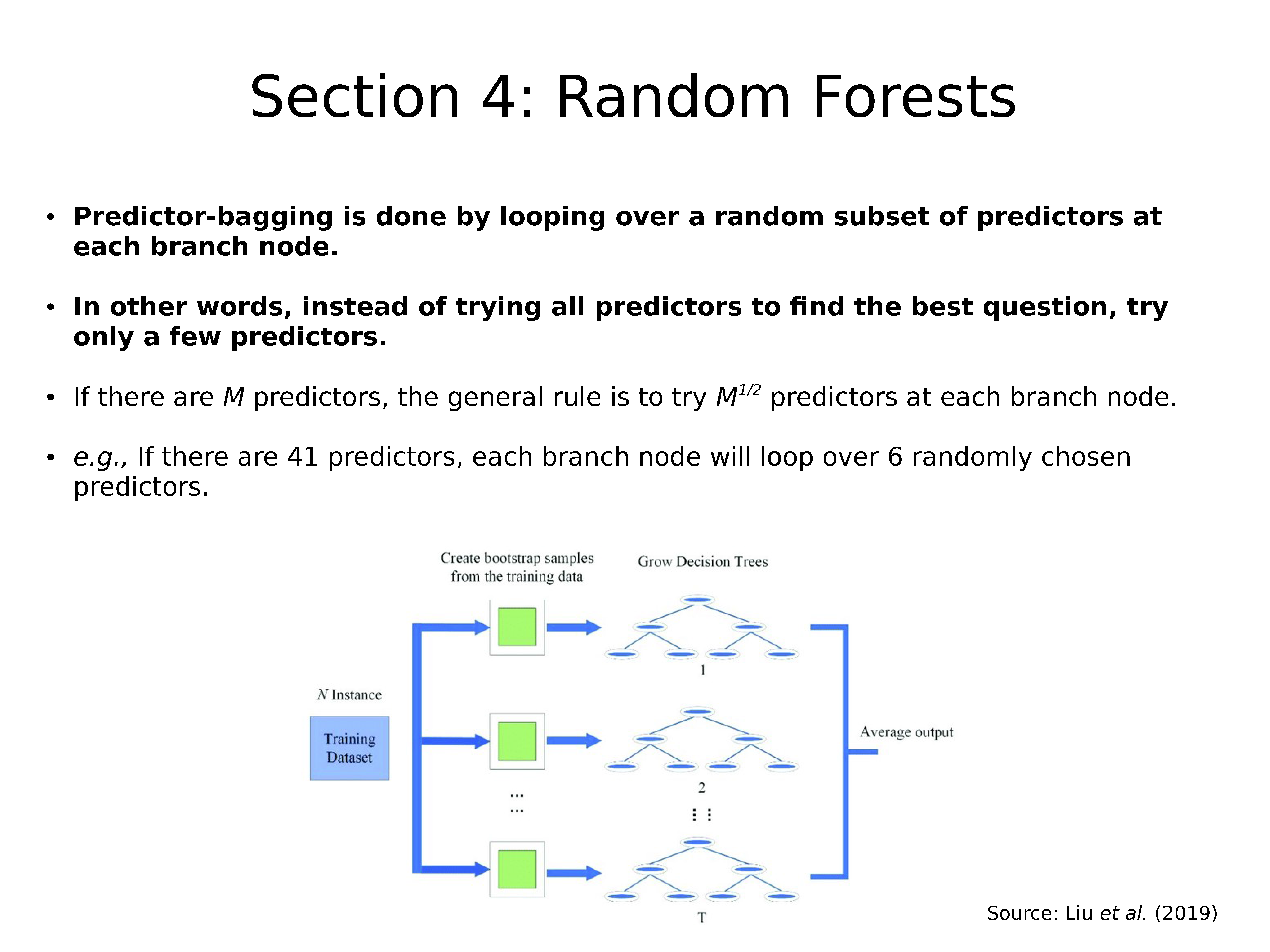
通过在每个分支节点上循环随机的预测变量子集来完成 Predictor-bagging。

换句话说，不要尝试所有预测变量找到最佳问题，而只尝试几个预测变量。

如果有 M 个预测变量，则一般规则是在每个分支节点尝试 M^(1/2) 个预测变量。

例如，如果有 41 个预测变量，则每个分支节点将循环遍历 6 个随机选择的预测变量。

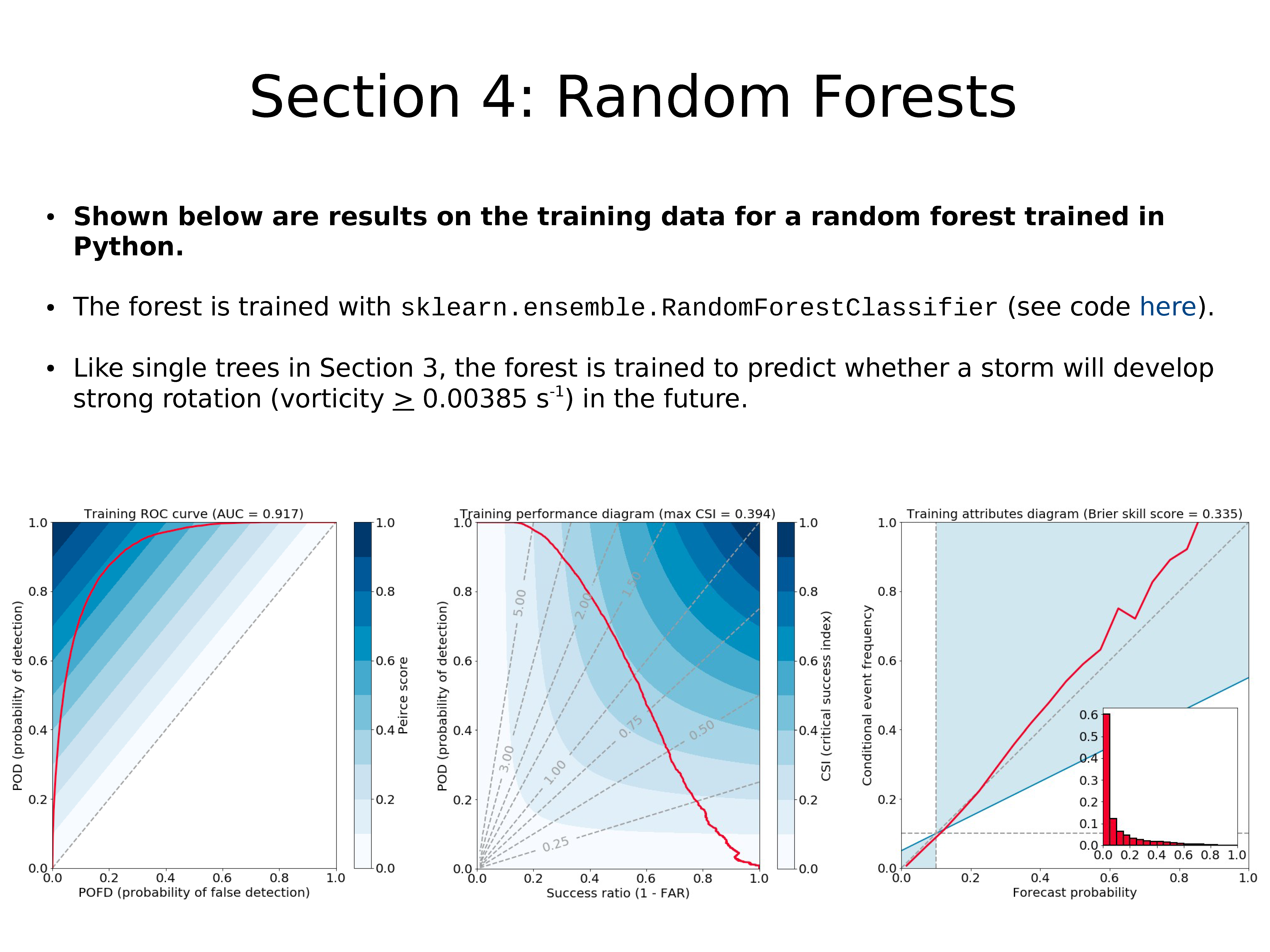
上面显示的是使用 Python 训练的随机森林的训练数据的结果。

使用 sklearn.ensemble.RandomForestClassifier 训练森林（代码）。

像上一节中的单棵树一样，对森林进行训练以预测未来暴风雨是否会形成强旋转（涡度 > 0.00385s-1）。

上图：同一森林在验证数据上的结果。

技巧上的很小变化表明，与单棵树不同，随机森林并没有严重过拟合：

  • AUC 下降 0.004
  • 最大 CSI（在性能图中显示）增加 0.007
  • Brier 技巧评分（在属性图中显示）下降 0.007
  • 这些差异可能都不具有统计学意义！

梯度提升森林

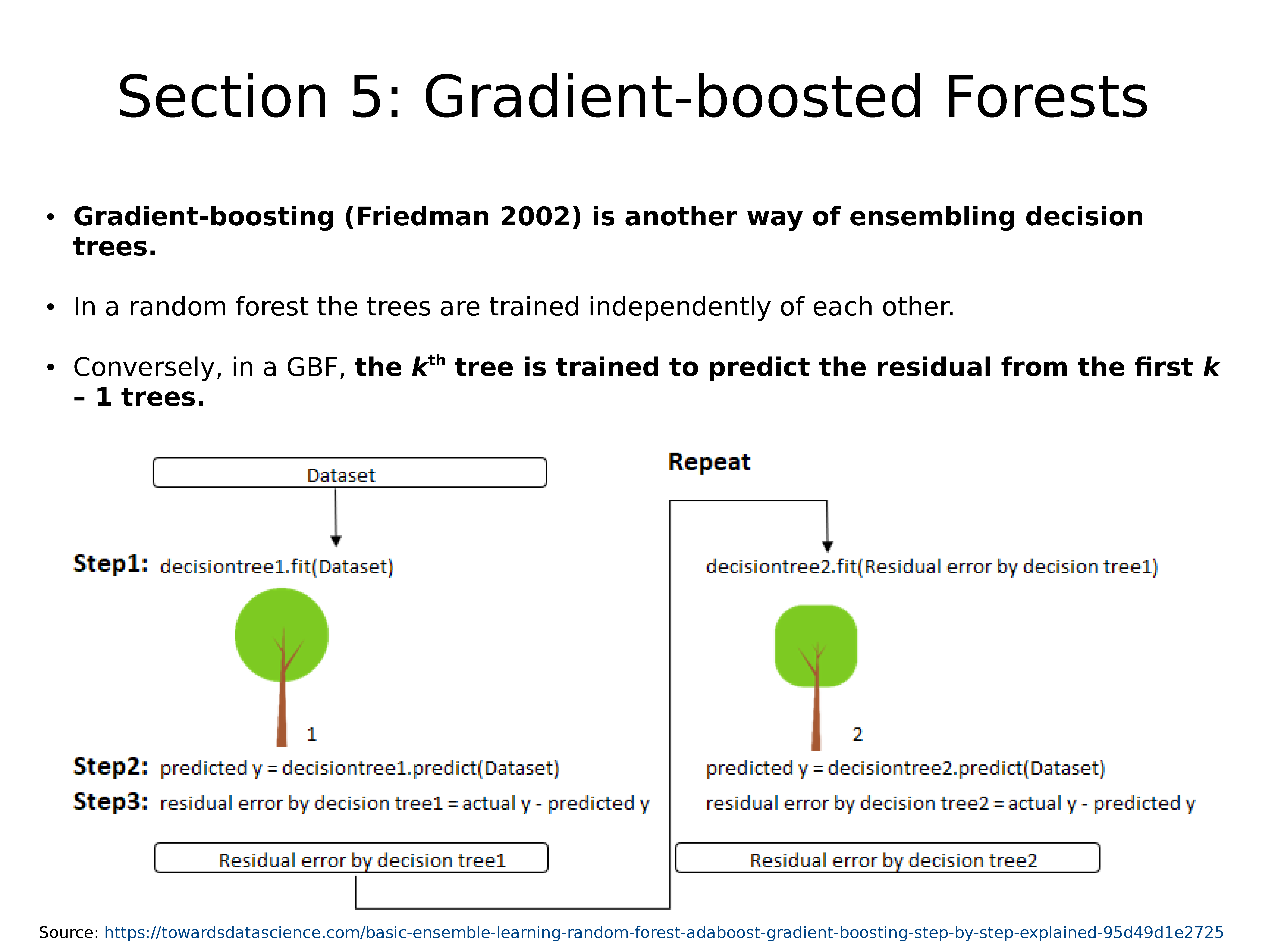
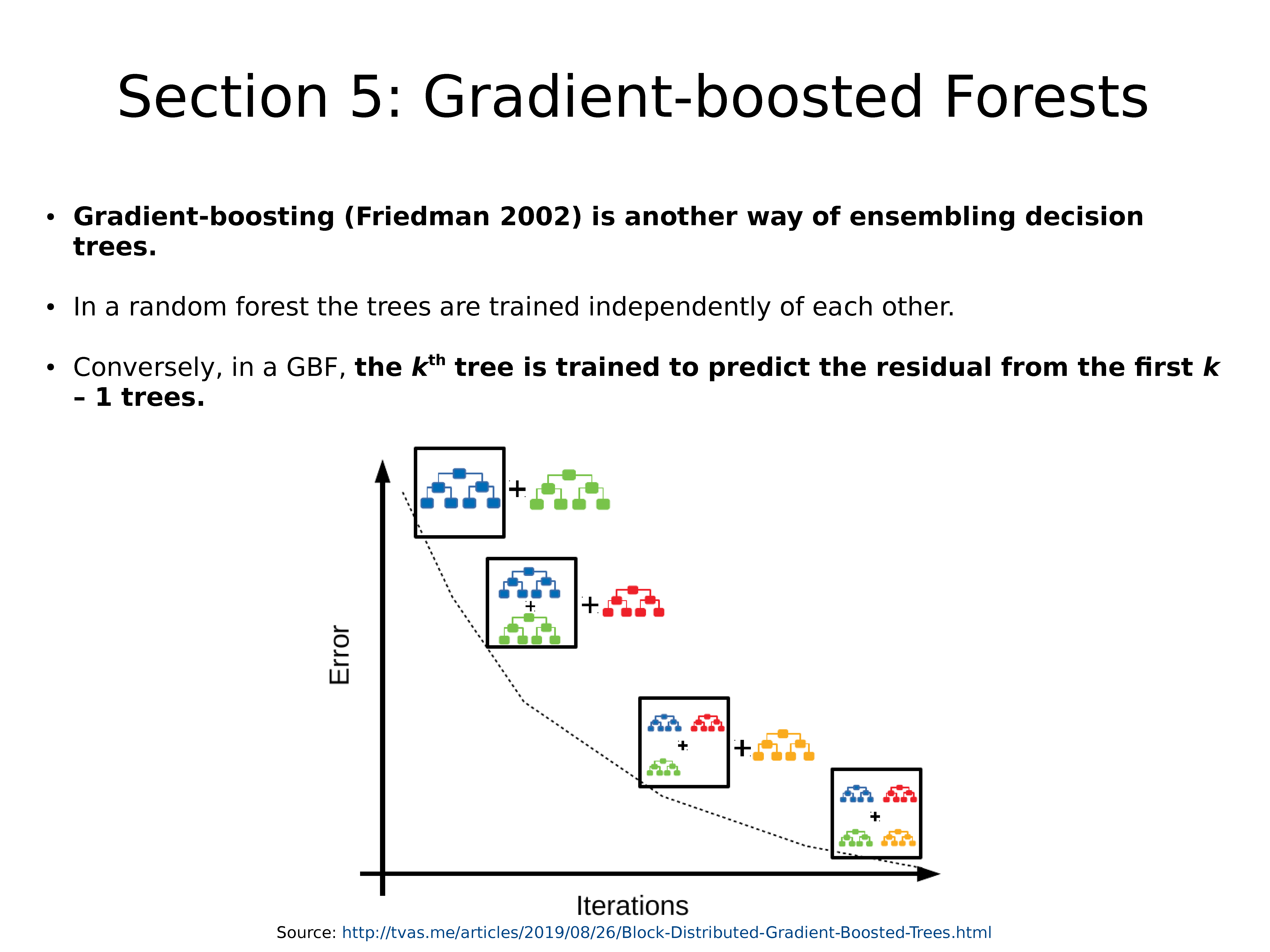
梯度增强（Gradient-boosting）（Friedman 2002）是组合决策树的另一种方法。

在随机森林中，树木彼此独立训练

相反，在GBF中，训练第 k 棵树以预测前 k-1 棵树的残差。

GBF 同样可以使用 example-bagging 和 predictor-bagging

但是，在大多数库中，默认设置都不使用 example-bagging 或 predictor-bagging。 而是使用所有样本训练每棵树，并在每个分支节点尝试所有预测变量。

在随机森林中，可以并行训练树木（每棵树木彼此独立），这使随机森林更快。

在GBF中，必须对树木进行串行训练，这会使它们变慢。

但是，实际上，GBF 通常会胜过随机森林。

在最近的太阳能预测竞赛中，排名前三的团队都使用了 GBF（McGovern等人，2015）。

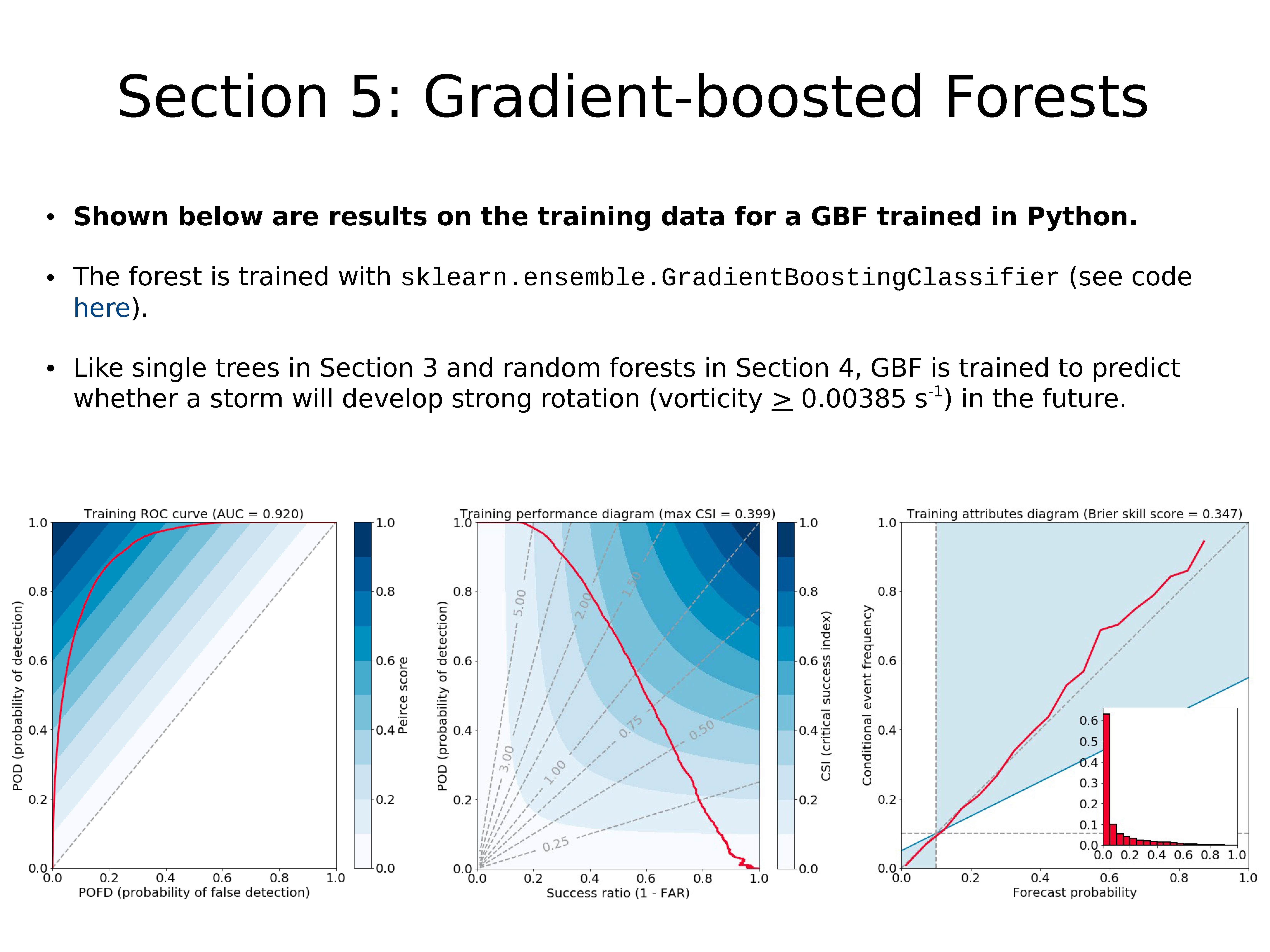
下面显示的是使用 Python 训练的 GBF 在训练数据上的结果。

使用 sklearn.ensemble.GradientBoostingClassifier 训练森林（代码）。

像上一节中的单棵树和本节中的随机森林一样，GBF 经过训练可以预测暴风雨将来是否会形成强旋转（涡度 > 0.00385s-1）。

上图：相同 GBF 在验证数据上的结果。

像随机森林一样，但与单树不同，GBF 并没有严重地过拟合：

  • AUC 下降 0.008
  • 最大 CSI（在性能图中显示）增加 0.001
  • Brier 技巧评分（在属性图中显示）下降 0.022
  • 这些差异可能都不具有统计学意义！

GBF 的验证结果比随机森林的验证结果稍差（但同样，差异可能并不明显）。

总结

决策树可以使用一系列是或不是问题来解决回归或分类问题

决策树的主要优点：可读性强

主要缺点：它们通常过拟合

可以通过使用随机或梯度增强的森林集合决策树来减轻过拟合情况。

森林的劣势：人类难以理解。虽然可以理解单个树，但森林通常有数百棵树

您可以在此处找到所有实验的交互式代码：

https://github.com/djgagne/ams-ml-python-course/blob/master/module_2/ML_Short_Course_Module_2_Basic.ipynb

决策树和森林在大气科学中的应用：

参考

Breiman, L., 2001: “Random forests.” Machine Learning, 45 (1), 5–32, https://link.springer.com/content/pdf/10.1023/A:1010933404324.pdf.

Chisholm, D., J. Ball, K. Veigas, and P. Luty, 1968: “The diagnosis of upper-level humidity.” Journal of Applied Meteorology, 7 (4), 613-619.

Friedman, J., 2002: “Stochastic gradient boosting.” Computational Statistics and Data Analysis, 38 (4), 367–378, https://www.sciencedirect.com/science/article/abs/pii/S0167947301000652.

McGovern, A., D. Gagne II, J. Basara, T. Hamill, and D. Margolin, 2015: “Solar energy prediction: An international contest to initiate interdisciplinary research on compelling meteorological problems.” Bulletin of the American Meteorological Society, 96 (8), 1388- 1395, https://journals.ametsoc.org/bams/article/96/8/1388/69447.

Quinlan, J., 1986: “Induction of decision trees.” Machine Learning, 1 (1), 81–106, https://link.springer.com/article/10.1007/BF00116251.

参考

https://www2.cisl.ucar.edu/events/summer-school/ai4ess/2020/artificial-intelligence-earth-system-science-ai4ess-summer-school

https://github.com/NCAR/ai4ess-hackathon-2020