AI4ESS 2020：机器和统计学习基础：实际应用
本文翻译自 AI4ESS 2020 课程，并有部分修改
Artificial Intelligence for Earth System Science (AI4ESS) Summer School
Machine and Statistical Learning Fundamentals
Dorit Hammerling - CSM / NCAR
实际应用
研究动机
大局：我们使用气候的自然变异性来模拟大气中一氧化碳（CO）浓度。
动机：为什么要费心为一氧化碳建模？
火灾是南半球二氧化碳的主要来源。
一氧化碳可以用作火灾的代理变量。
预测性 CO 模型可以帮助各国为大规模火灾事件做准备。
响应变量
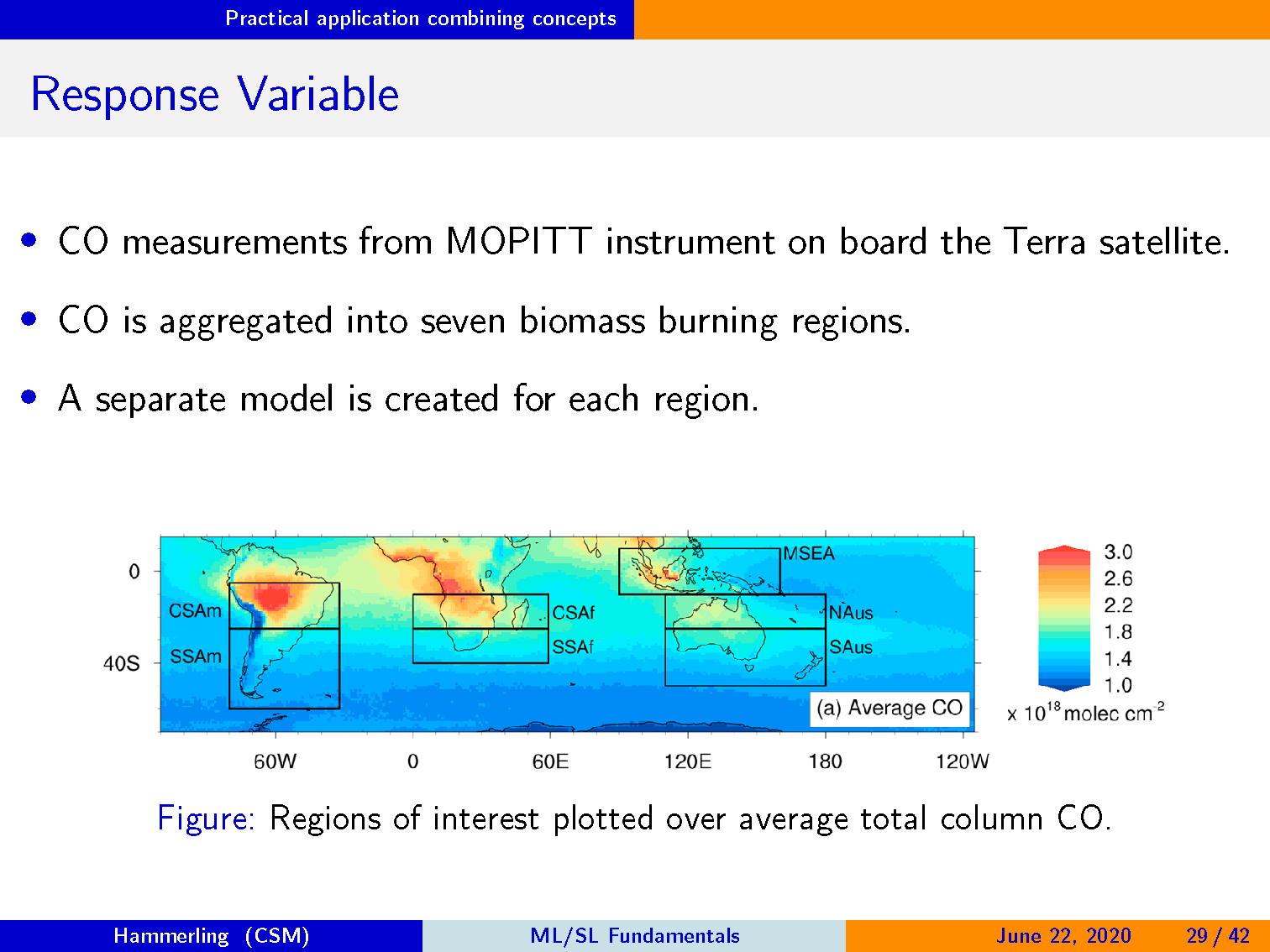
Terra 卫星上来自 MOPITT 仪器的 CO 测量。
CO 聚集到七个生物质火灾区。
为每个区域创建独立的模型。
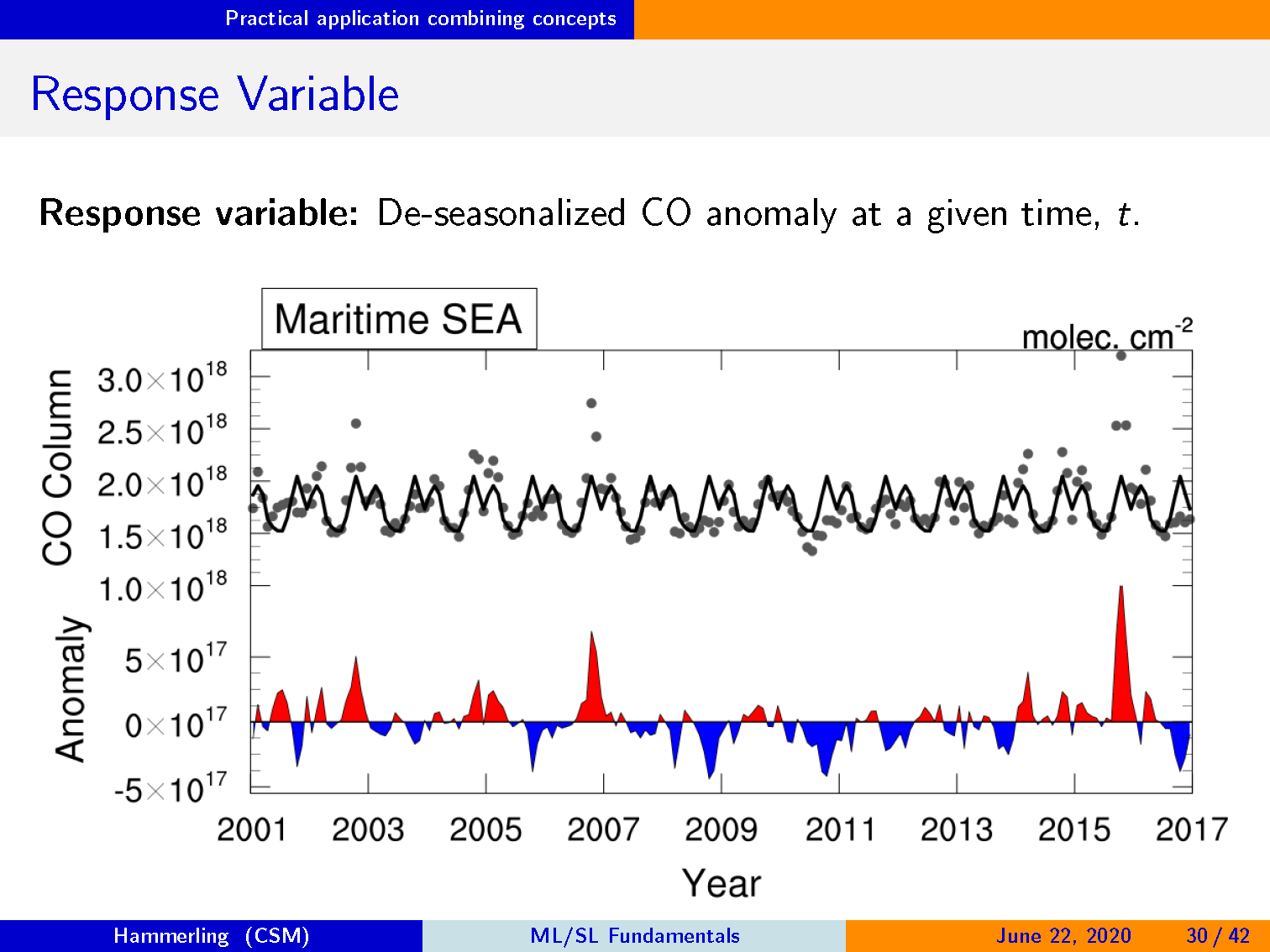
响应变量：给定时间 t 的反季节化的 CO 异常。
预测变量
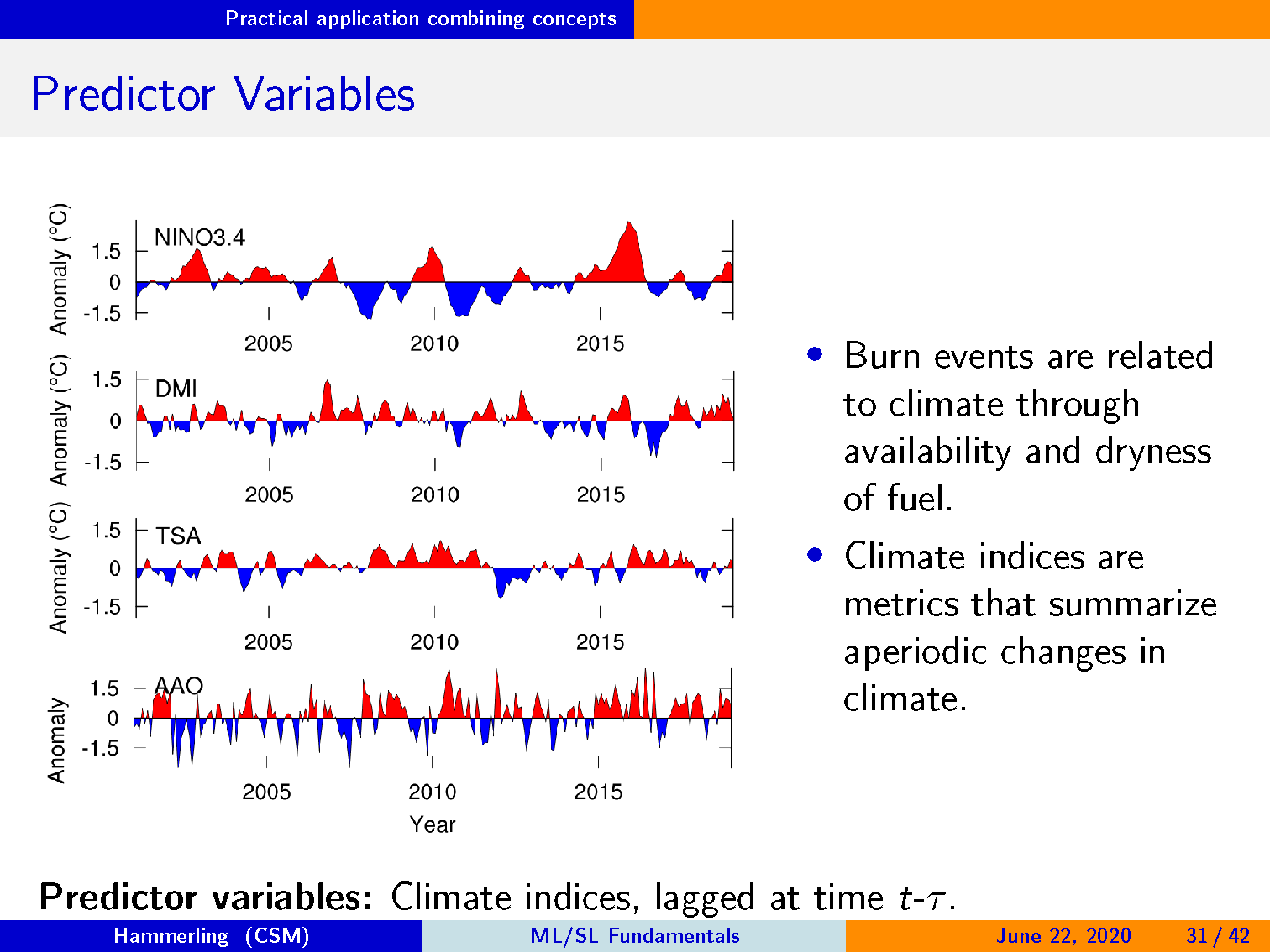
火灾事件通过燃料的可用性和干燥度与气候相关。
气候指数是总结气候非周期性变化的指标。
预测变量：气候指数，滞后t
统计模型
我们使用具有一阶相互作用项的滞后多元线性回归模型来解释大气 CO 与气候指数之间的关系。
$$ CO(t)=\mu + \sum_{k}^{}a_{k}\cdot \chi_{k}(t-\tau_{k}) + \sum_{i,j}^{}b_{ij}\cdot\chi_{i}(t-\tau_{i})\cdot\chi_{j}(t-\tau_{j}) $$
CO（t）是时间 t 处给定响应区域中的 CO 异常
u是恒定的平均位移
ak 和 bij 是系数
X 是气候指数
T 是每个指数的滞后值
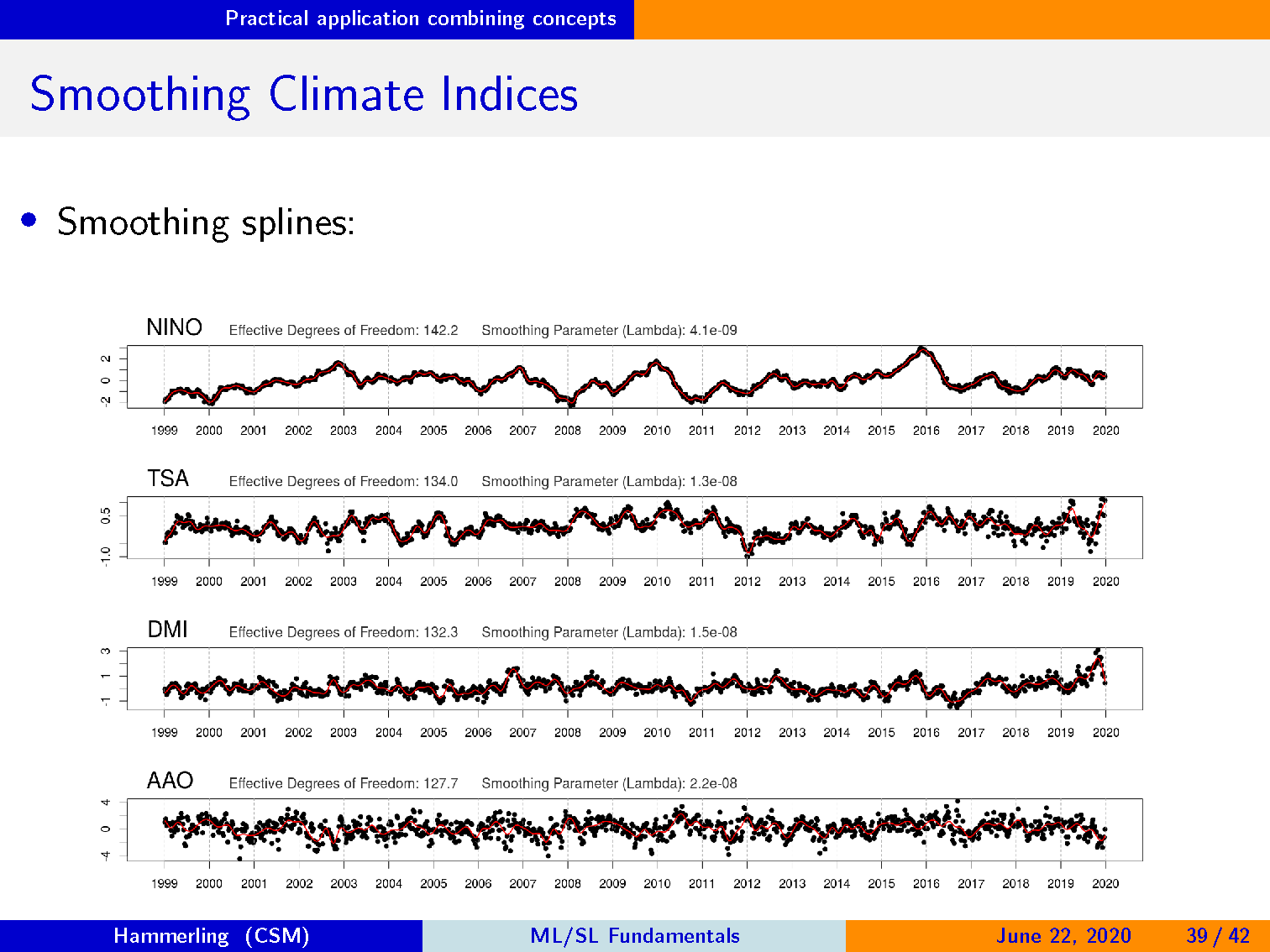
气候指数的变化
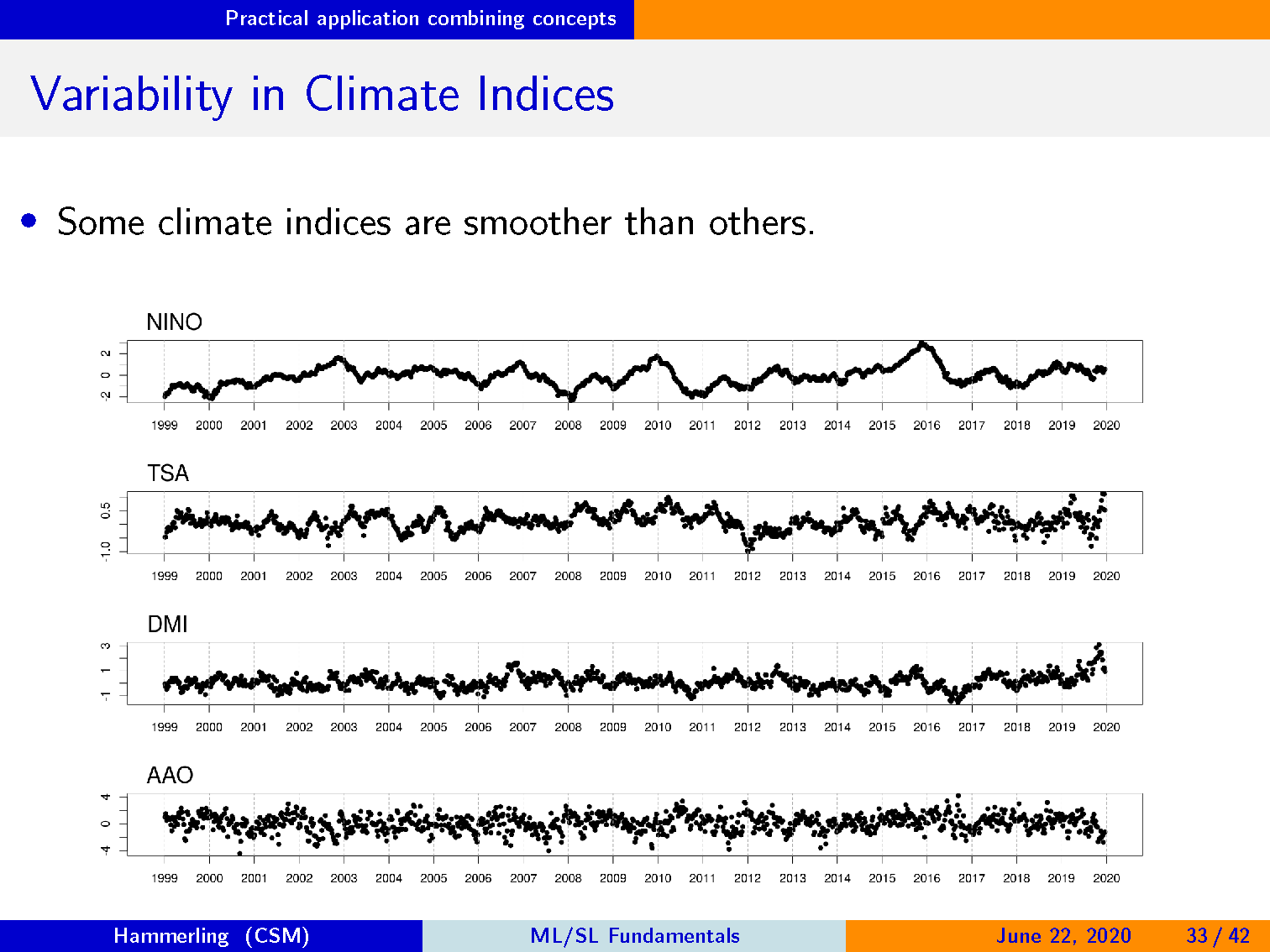
一些气候指数比其他气候指数更平滑。
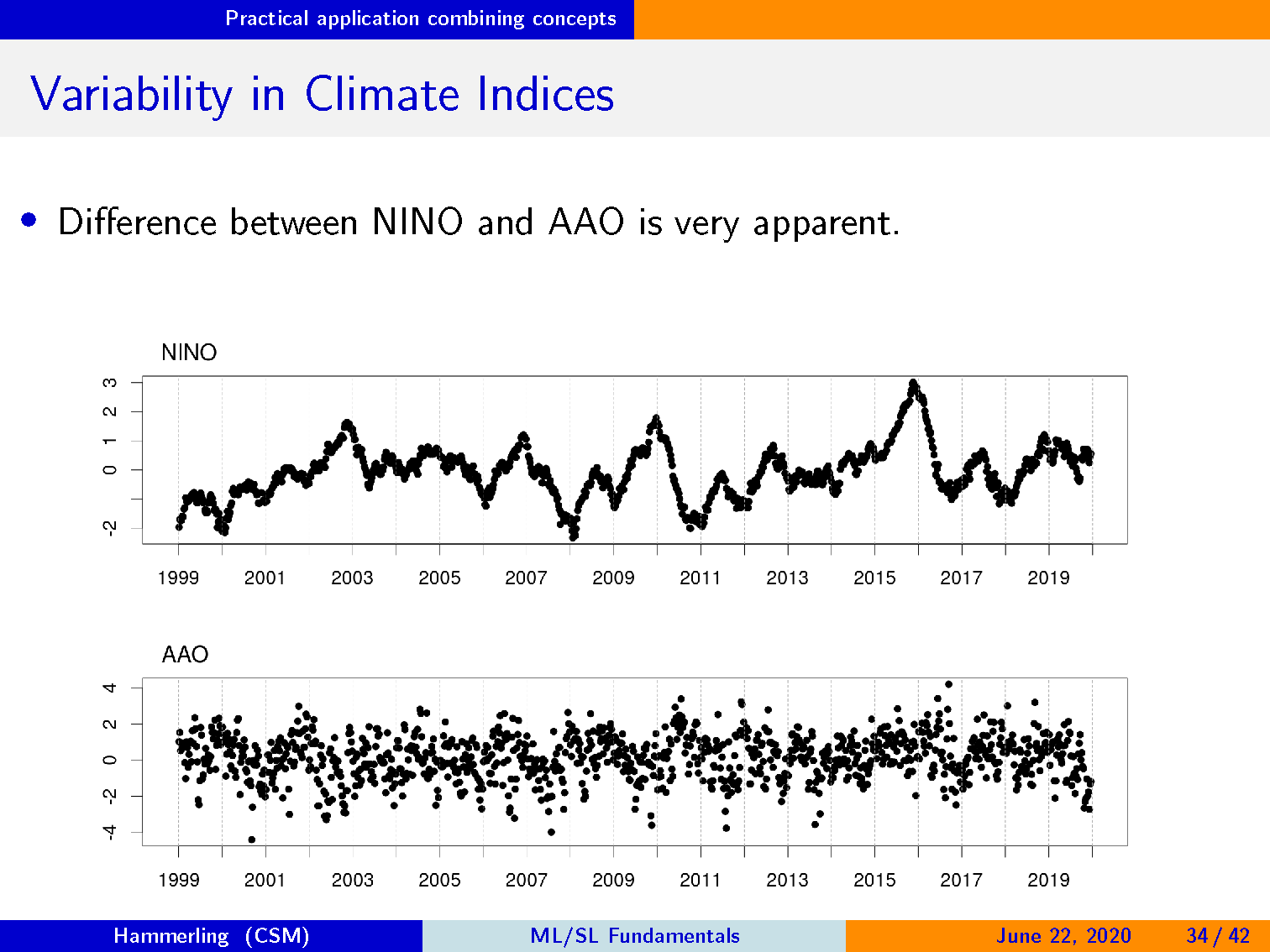
NINO 和 AAO 之间的区别非常明显。
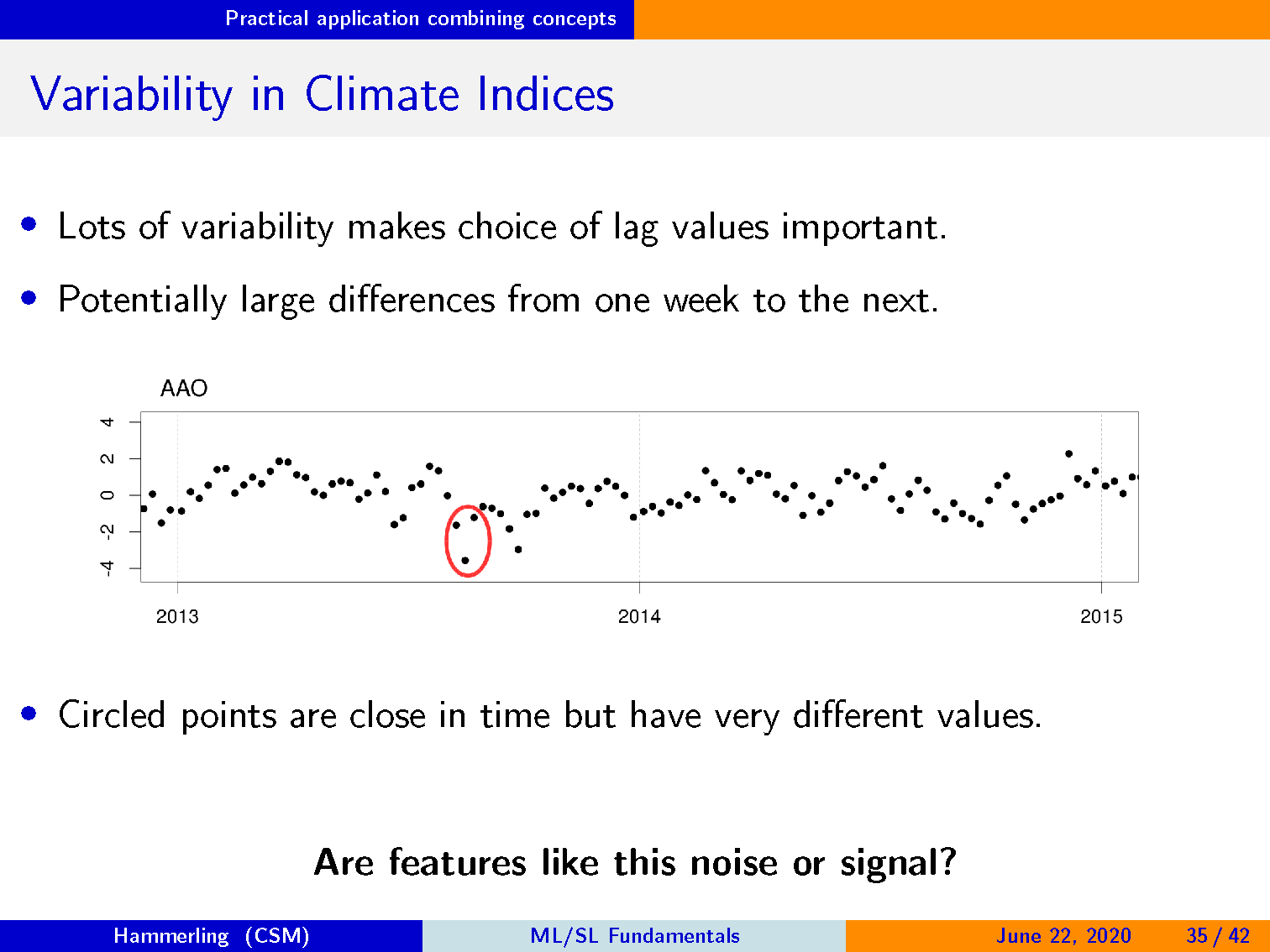
大量的可变性使得滞后值的选择很重要。
从一周到下一周可能存在很大差异。
带圆圈的点在时间上接近，但具有非常不同的值。
像这样的特征是噪声还是信号？
平滑气候指数
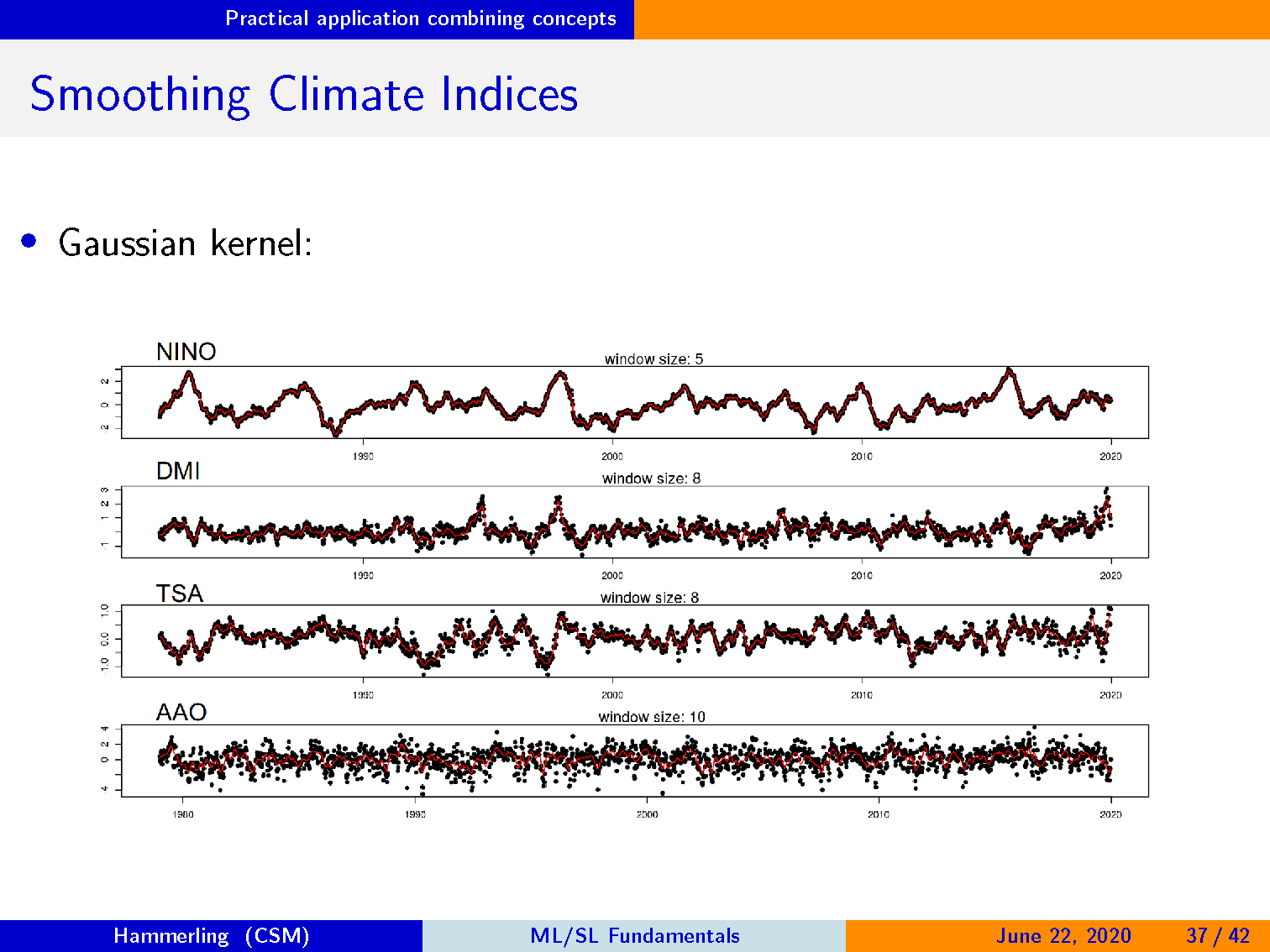
平滑的气候指数可以防止这些嘈杂的跳跃。
平滑内核：
在数据上移动平均“窗口”。
将权重应用于平均值，以使当前数据点影响最大。
高斯核：
$$ K(t)=\frac{1}{\sqrt{2\pi }}exp(-t^{2}/2) $$
其中参数 t 控制平滑窗口的大小
通常使用交叉验证来选择窗口大小
平滑样条线：
优化 “损失 + 惩罚” 形式的损失函数
损失项鼓励平滑样条，以很好地适应数据。
惩罚项可防止平滑样条过度拟合。
寻找函数 f，最小化：
$$ \sum_{i=1}^{n}(y_{i}-f(x_{i}))^{2}+\lambda\int {{f}’’}(t)^{2}dt $$
调整参数 labmda 平衡损失和惩罚项。
通常通过交叉验证选择调整参数。
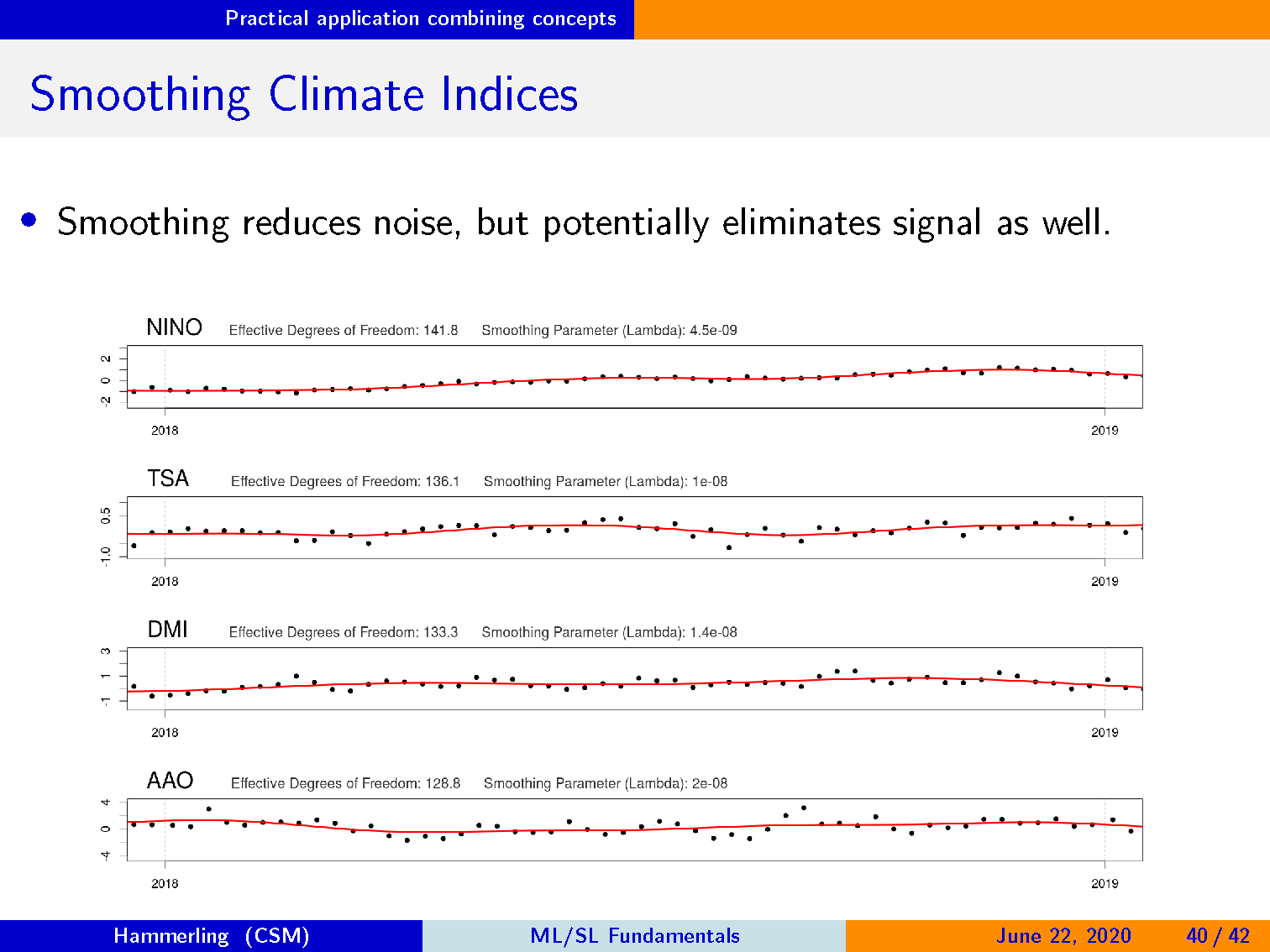
平滑可减少噪声，但也可能消除信号。
模型性能
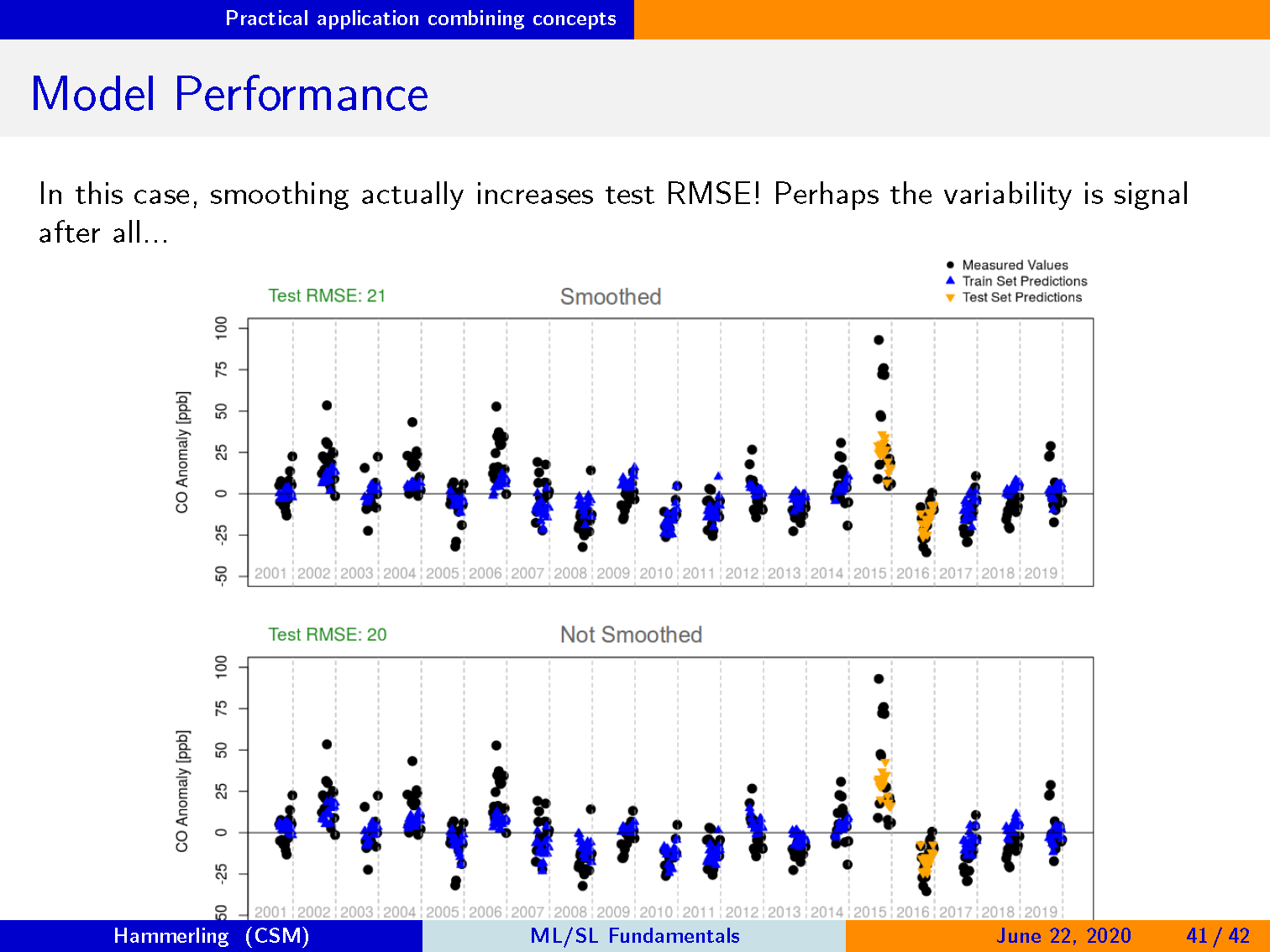
在这种情况下，平滑实际上会增加测试 RMSE！ 毕竟变异性也许是信号…
参考
参考
https://github.com/NCAR/ai4ess-hackathon-2020
