AI4ESS 2020:机器和统计学习基础:函数形式,交叉验证和模型选择
本文翻译自 AI4ESS 2020 课程,并有部分修改
Artificial Intelligence for Earth System Science (AI4ESS) Summer School
Machine and Statistical Learning Fundamentals
Dorit Hammerling - CSM / NCAR

函数形式,交叉验证和模型选择

如何估算 f

回忆下模型的最简单形式:
$$ Y = f(X) + \epsilon $$
估算 \(\hat{f}\) 的目标:
寻找一个函数 \(\hat{f}\),对于所有的 (X, Y) 都有 \(Y\approx\hat{f}(X)\)
虽然具体细节依赖于特定的方法,但仍有一些通用的特性我们可以讨论。
为了这样做,我们将方法分为参数化方法(例如使用函数形式)和非参数化方法。
参数化方法

参数化建模包括两个步骤:
- 假设函数形式
线性模型是一个简单的示例:
\begin{equation*} f(X)=\beta_{0}+\beta_{1}*X_{1}+\beta_{2}*X_{2}+…+\beta_{p}X_{p} \end{equation}
估算 f 问题现在简化为估算参数 \(\beta_{0},\beta_{1},\beta_{2},…,\beta_{p}\)
- 使用 训练数据 估计参数,用于拟合或训练模型
取决于函数的形式和参数的个数,这个步骤可能在数值上具有挑战性。 在简单的情况下,例如线性模型,有明确的解决方案,例如最小二乘法。
非参数化方法

非参数化模型没有对 f 的函数形式做出明确的假设。 相反,它们的目标是在符合平滑度约束的同时,估算接近数据的 f。
关键点:
非参数方法的主要优点是,它们不施加特定的函数形式,函数可能与真实 f 相距甚远。
它们的主要缺点是所需观察的次数很多,因为它们没有将估计 f 的问题减少到少量参数。 它们在推断中也不是很有帮助。
需要确定使数据拟合度与平滑度约束平衡的参数。
解释参数化(线性)模型
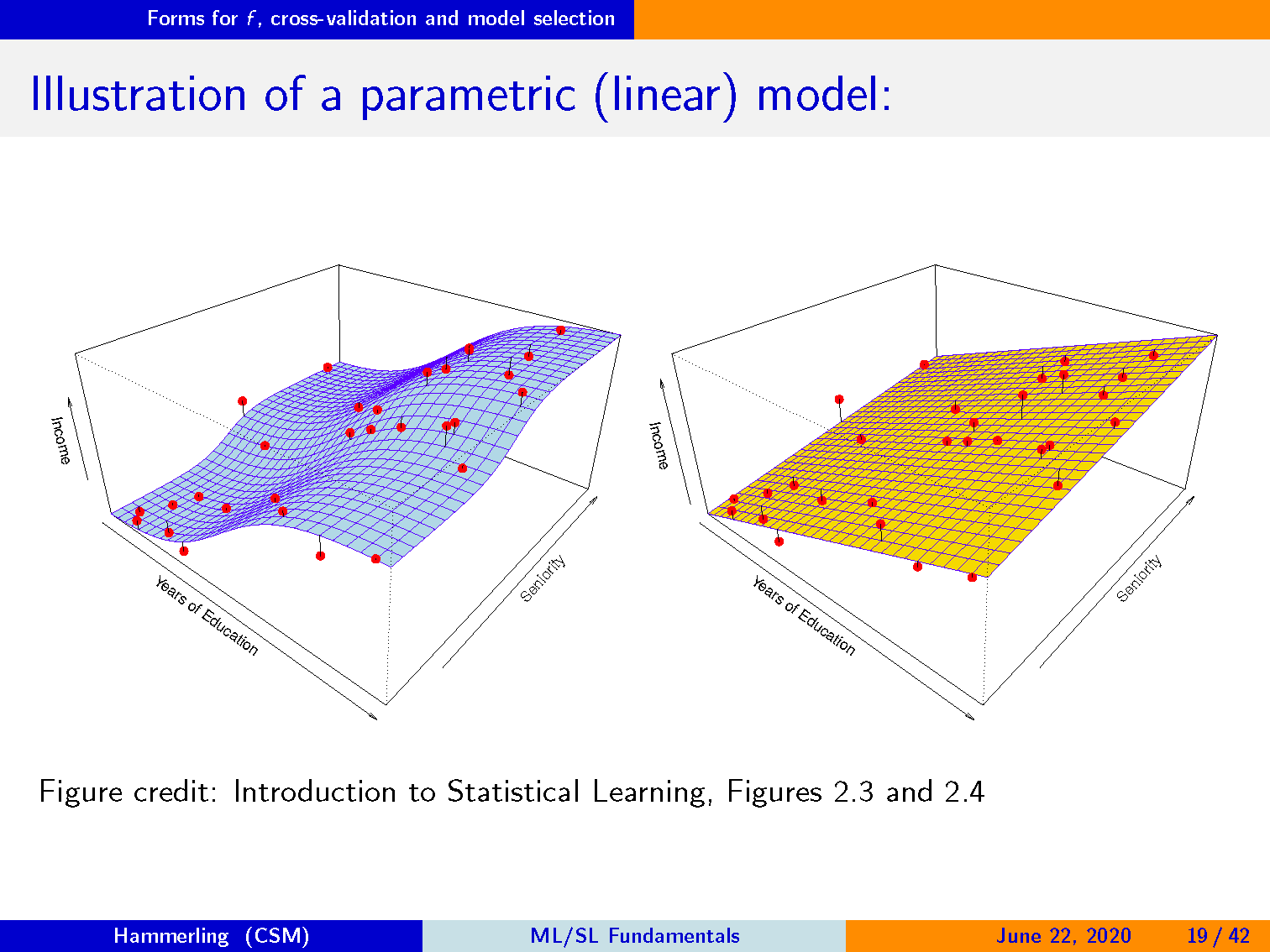
解释非参数化模型(薄板样条插值)
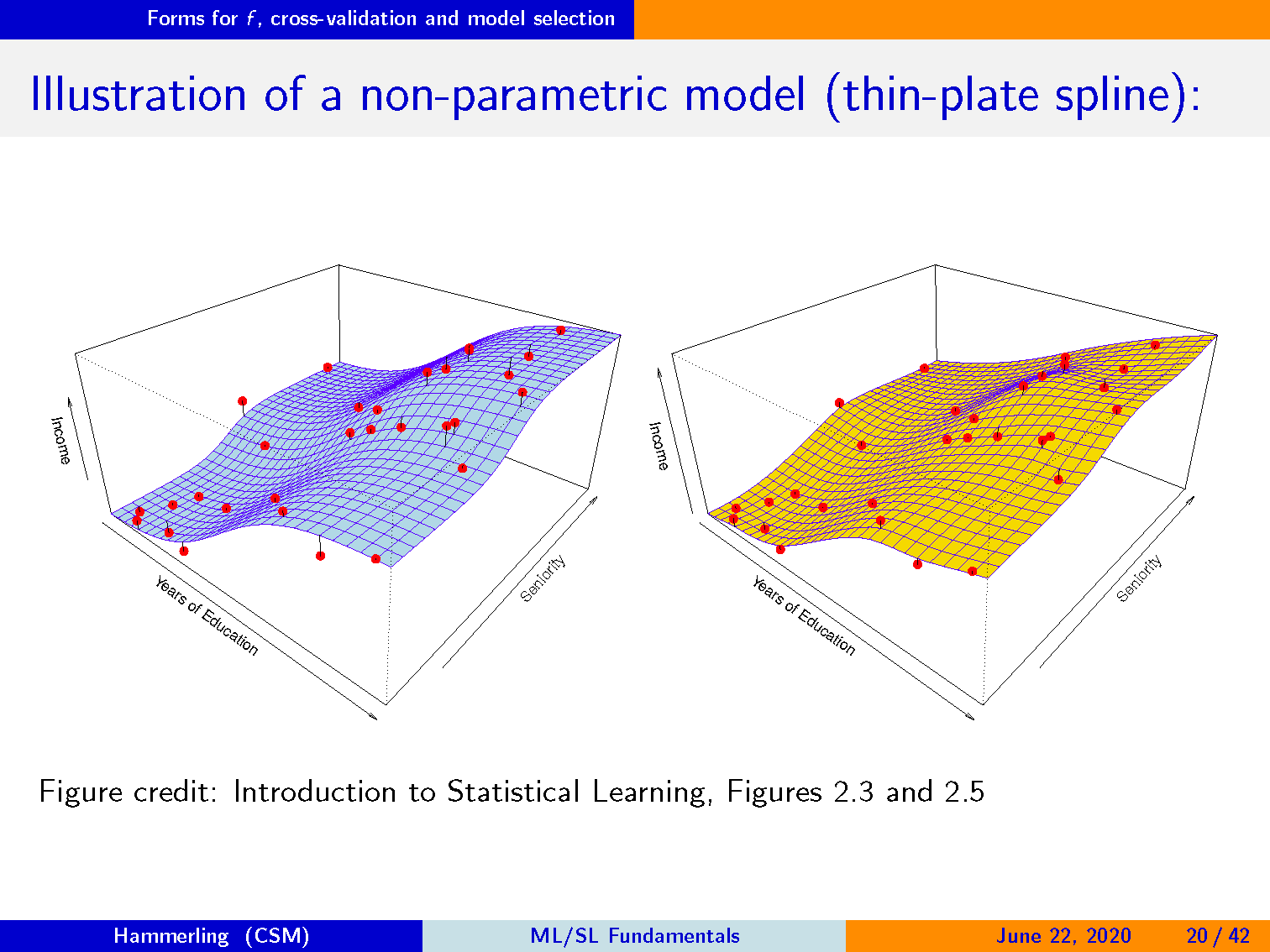
比较不同的平滑假设
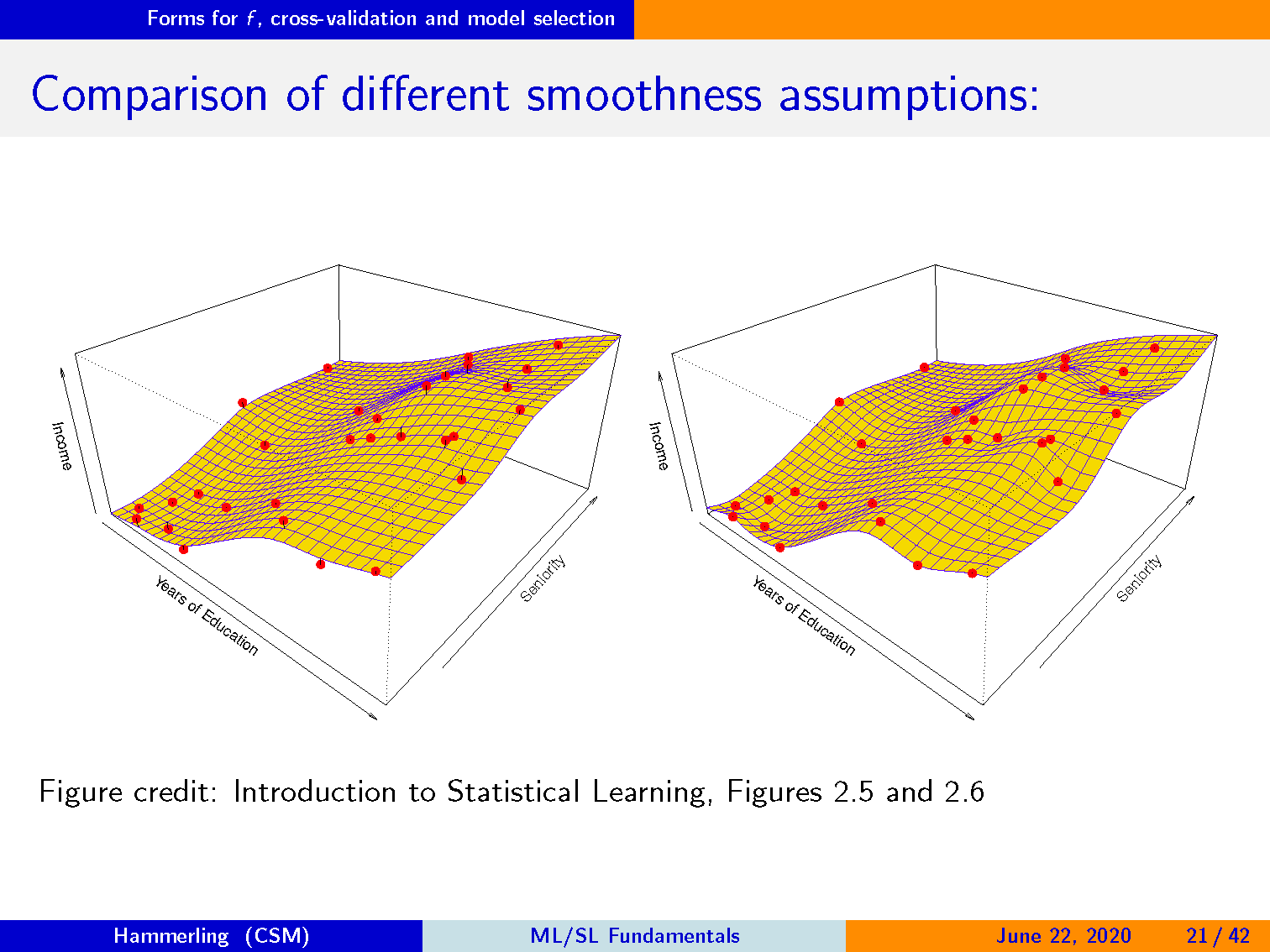
我们如何估算调整参数?

交叉验证通常都是想要的答案。
交叉验证的主要思想是将数据分为 训练数据 和 测试数据。 顾名思义,我们使用 训练数据 训练 模型,并使用 测试数据 评估 其在新数据上的性能。
我们不想只使用训练数据来评估我们的模型,因为这种方法会自动支持更灵活的模型。
可以将对训练数据的合理考虑认为是必要但不是充分的条件,而对新数据的表现是石蕊测试(litmus test)。
交叉验证的用途非常广泛,可以在各种设置中用于评估模型或参数!
解释训练误差和测试误差

第一幅图是训练数据和拟合曲线,第二幅图中灰色曲线是拟合函数在训练数据集上的 MSE,红色曲线是在测试数据集上的 MSE。
第一幅图中的黑色线是理论分布函数,实际数据会有随机误差。
黄色曲线是线性拟合的结果,观察第二幅图中的黄点可以发现,线性拟合的训练误差和测试误差都很大,这是欠拟合。
蓝色曲线和绿色曲线是两种平滑样条曲线拟合,其中蓝色曲线的训练误差和测试误差比较接近,是一个可以接收的模型。 而绿色曲线虽然训练误差很小,但测试误差很大,这属于过拟合。
交叉验证的主要方式

留一法交叉验证(LOOCV):单个观察包括验证集,其余数据用于训练。
$$ CV_{(n)}=\frac{1}{n}\sum_{i=1}^{n}MSE_{i} $$
如果模型很复杂,计算可能会非常昂贵。
k 折交叉验证:数据随机分为 k 组。 第一组视为验证数据,其余组视为训练数据。 重复 k 次以切换验证集。
$$ CV_{(k)}=\frac{1}{k}\sum_{k=1}^{n}MSE_{i} $$
LOOCV是 k = n 的 k 折交叉验证的特例。
解释交叉验证

