NWPC笔记:预测模式积分时长 - 线性回归
上一篇文章《NWPC笔记:分析模式积分时长 - 线性回归》中介绍如何使用线性回归拟合模式积分单步耗时,训练数据使用的是数据全集。
但在实时业务中,我们往往需要尽可能早地判断模式积分是否异常,也就需要在模式积分过程中使用已完成的积分步骤时间来预测积分结束时间。
本文介绍使用线性回归预测模式积分时长,对比使用不同的数据量作为训练集对最终预测结果的影响。
声明:本文仅代表作者个人观点,所用数据无法代表真实情况,严禁转载。关于模式系统的相关信息,请以官方发布的信息及经过同行评议的论文为准。
获取数据
和上一篇文章一样,使用 nwpc-oper/nwpc-log-tool 获取单步积分数据。
创建函数,批量获取运行时间。
def get_cum_time(start_time_list):
data = dict()
for start_time in start_time_list:
file_path = find_local_file(
"grapes_gfs_gmf/log/fcst_long_std_out",
start_time=start_time,
)
df = get_step_time_from_file(file_path)
df["ctime"] = df["time"].cumsum()
data[start_time] = df["ctime"]
df = pd.DataFrame(
data,
index=df.index
)
return df获取 2020 年 4 月 10 日至 2020 年 4 月 30 日的数据,并输出积分总时间(单位:秒)
df = get_cum_time(
pd.date_range(
"2020-04-10",
"2020-04-30",
freq="D",
)
)
df.iloc[-1] / 602020-04-10 23.170123
2020-04-11 23.935507
2020-04-12 22.960625
2020-04-13 44.652387
2020-04-14 23.098123
2020-04-15 22.748205
2020-04-16 22.902938
2020-04-17 23.128332
2020-04-18 23.376948
2020-04-19 23.527448
2020-04-20 22.829743
2020-04-21 32.210792
2020-04-22 29.892152
2020-04-23 23.042733
2020-04-24 22.938663
2020-04-25 22.867722
2020-04-26 22.937087
2020-04-27 31.016060
2020-04-28 32.708422
2020-04-29 31.268345
2020-04-30 22.859272
Name: 2880, dtype: float64
从下面的图形可以看到有几天的积分耗时明显异常。
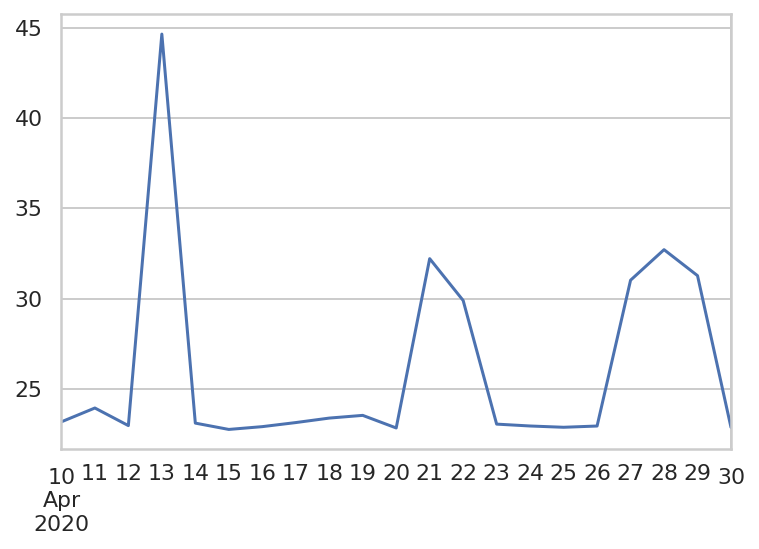
计算线性回归
创建函数,根据截取已积分的天数(days)训练线性回归模型
def get_linear_models(df, days):
models = []
sample_number = 12 * 24 * days
for a in df:
X = df[a].index.values.reshape(-1, 1)
y = df[a]
reg = linear_model.LinearRegression()
reg.fit(X[:sample_number], y[:sample_number])
models.append({
"col": a,
"model": reg,
})
return models从第 1 天到第 10 天,每隔一天训练一个线性回归模型
days_list = range(1, 11)
total_end_times = {}
total_coefs = {}
total_bias = {}
for days in days_list:
models = get_linear_models(df, days)
end_times = []
coefs = []
for model in models:
end_time = model["model"].predict(np.reshape(2880, (-1, 1)))[0]/60
end_times.append(end_time)
coefs.append(model["model"].coef_[0])
bias = end_times - df.iloc[-1]/60
coefs = pd.Series(coefs, index=bias.index)
total_end_times[days] = end_times
total_bias[days] = bias
total_coefs[days] = coefs
end_times_df = pd.DataFrame(total_end_times, index=df.iloc[-1].index)
bias_df = pd.DataFrame(total_bias)
coefs_df = pd.DataFrame(total_coefs)coefs_df 是拟合直线的斜率,绘制所有的斜率
fig, ax = plt.subplots(figsize=(15, 5))
coefs_df.plot(
cmap="viridis",
ax=ax,
)
上图中斜率越大的日期,多次拟合的斜率差别越大,但无论使用 1 天的数据还是 10 天数据,都能很好地区分积分正常和积分异常的情况。
end_times_df 是预测的积分结束时间,列名称表示使用多少天的训练数据。
end_times_df.head()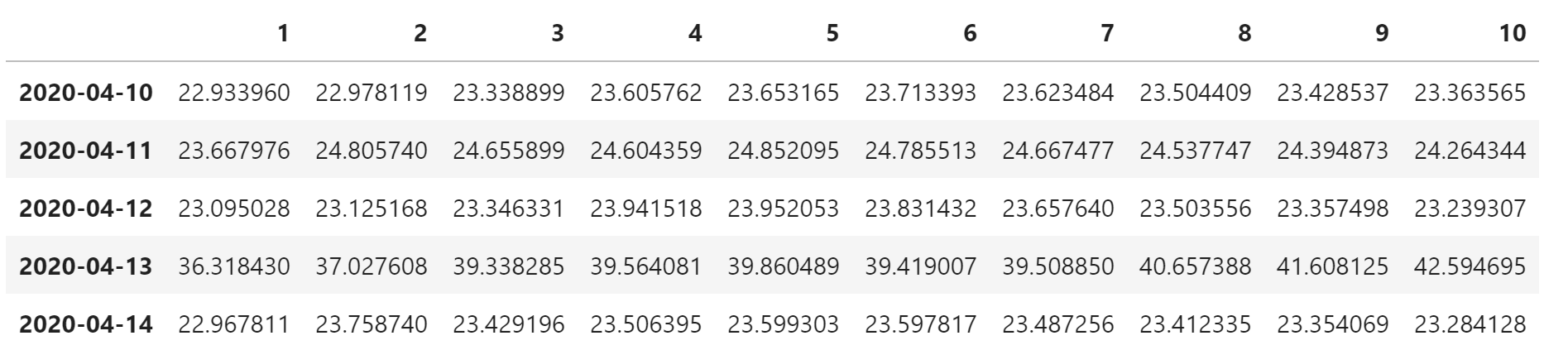
绘制所有的预测积分结束时间,并用红色线绘制实际的积分时长。
fig, ax = plt.subplots(figsize=(15, 5))
end_times_df.plot(
cmap="viridis",
ax=ax
)
(df.iloc[-1]/60).plot(
color="red",
ax=ax
)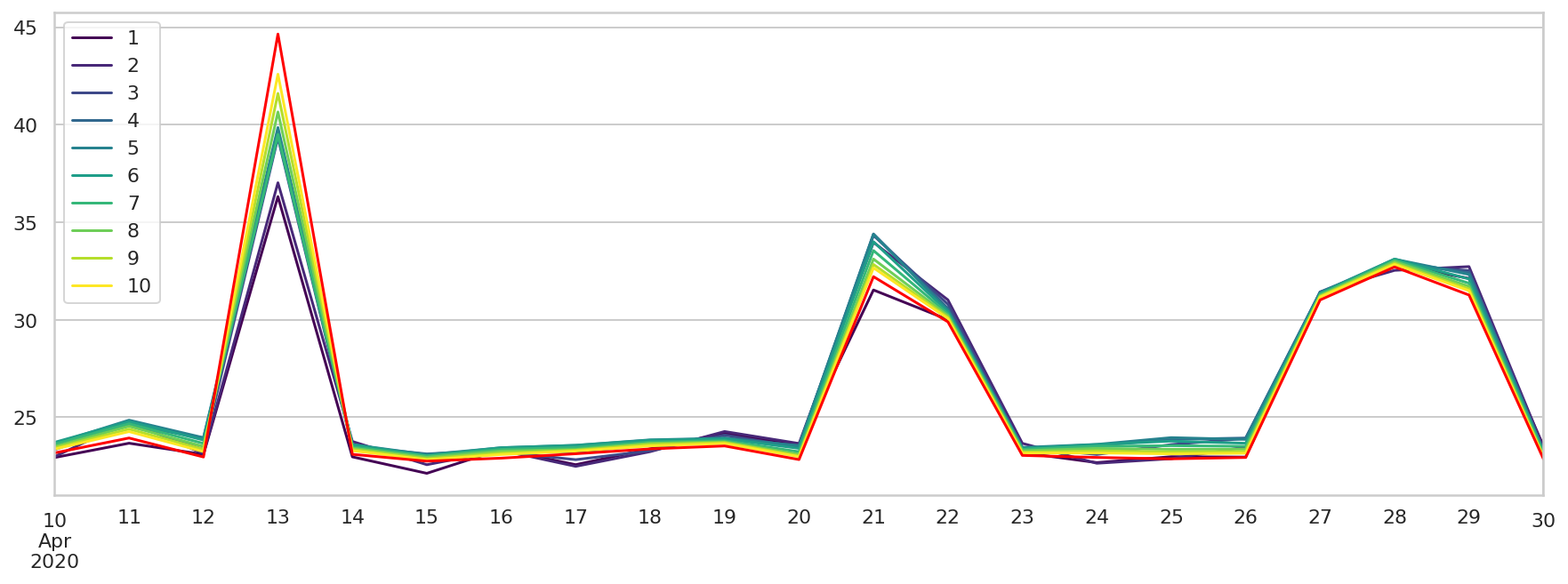
对于积分正常的时次,拟合结果一般都在 25 分钟以下,而对于积分异常的时次,拟合结果差别比较大,但都在异常范围内。
bias_df 是拟合结果与实际数据的偏差,绘图显示所有的偏差
fig, ax = plt.subplots(figsize=(15, 5))
bias_df.plot(
cmap="viridis",
ax=ax,
)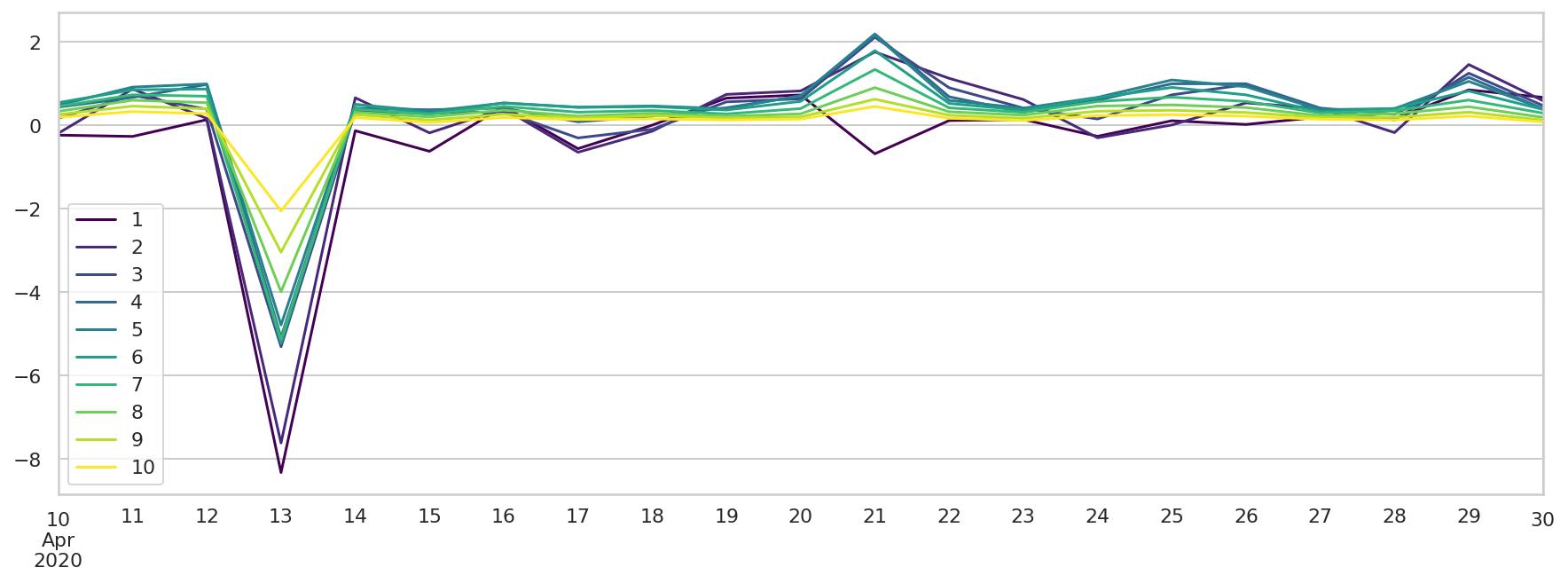
绝大部分的时次,偏差都在 2 分钟以内,相对于 20 分钟的模式积分时长来说,我们还是可以接受的。
总结
从上面的分析可以看到,即使仅使用第 1 天的数据进行预测,也可以得到定性的结论。 随着使用数据越来越多,预测精度会逐渐提高。
后续笔者会尝试构建实时预测系统,来验证本文的方法是否满足业务监控的需求。
