统计数值预报产品生成时间:单个时效重采样
目录
前一篇文章《统计数值预报产品生成时间:单个时效》中介绍使用切尾均值作为产品生成的典型时间。对于单个时效的特定产品,即便将时间范围延长到一年,也仅有365个数据。 如果考虑系统升级可能带来的影响,可用的数据点就会更少。 数据量较少时,单纯使用均值会受到离群值的影响,所以前一篇文章中使用切尾均值作为典型时间。
本文介绍另外一种思路。我们可以增加样本数,而自助法(Bootstrap)正是可以实现这一目标的工具。
声明:本文仅代表作者个人观点,所用数据无法代表真实情况,严禁转载。关于模式系统的相关信息,请以官方发布的信息及经过同行评议的论文为准。
数据
使用与《统计数值预报产品生成时间:单个时效》相同的数据,不再介绍。
计算
重采样 20 个样本,计算均值,并重复指定次数 count
count = 10000
means = []
for i in tnrange(count):
sampled_data = df.sample(n=20, replace=True)
means.append(sampled_data.mean())将所有值近似到秒
bdf = pd.DataFrame(means).applymap(lambda x: x.ceil("s"))
bdf.head()| clock | |
|---|---|
| 0 | 04:50:53 |
| 1 | 04:56:04 |
| 2 | 05:02:03 |
| 3 | 04:48:51 |
| 4 | 04:53:21 |
计算采样均值的均值和方差
bdf_mean = bdf["clock"].mean()
bdf_meanTimedelta('0 days 04:53:28.601400')
bdf_std = bdf["clock"].std()
bdf_stdTimedelta('0 days 00:03:23.675759')
计算 95% 分位数,即 95% 置信区间
qt = bdf.quantile(
0.95,
numeric_only=False,
interpolation="nearest"
)
qtclock 04:59:37
Name: 0.95, dtype: timedelta64[ns]
将 bdf_mean + bdf_std 作为警告标准,将 qt["clock"] 作为延迟标准。
生成 status 列保存对 clock 列的分类。
warn_upper_value = bdf_mean + bdf_std
late_upper_value = qt["clock"]
def get_status(clock):
if clock > late_upper_value:
return "late"
elif clock > warn_upper_value:
return "warn"
else:
return "normal"
df["status"] = df["clock"].map(get_status)
df["start_time"] = df.index.map(lambda x: x.strftime("%m/%d"))
df.head()| clock | status | start_time |
|---|---|---|
| 2020-02-29 | 05:28:28 | late |
| 2020-03-01 | 05:22:41 | late |
| 2020-03-02 | 05:09:02 | late |
| 2020-03-03 | 04:39:53 | normal |
| 2020-03-04 | 05:30:53 | late |
绘图
使用与《统计数值预报产品生成时间:单个时效》相同的绘图方法,不再介绍。
绘图结果如下:
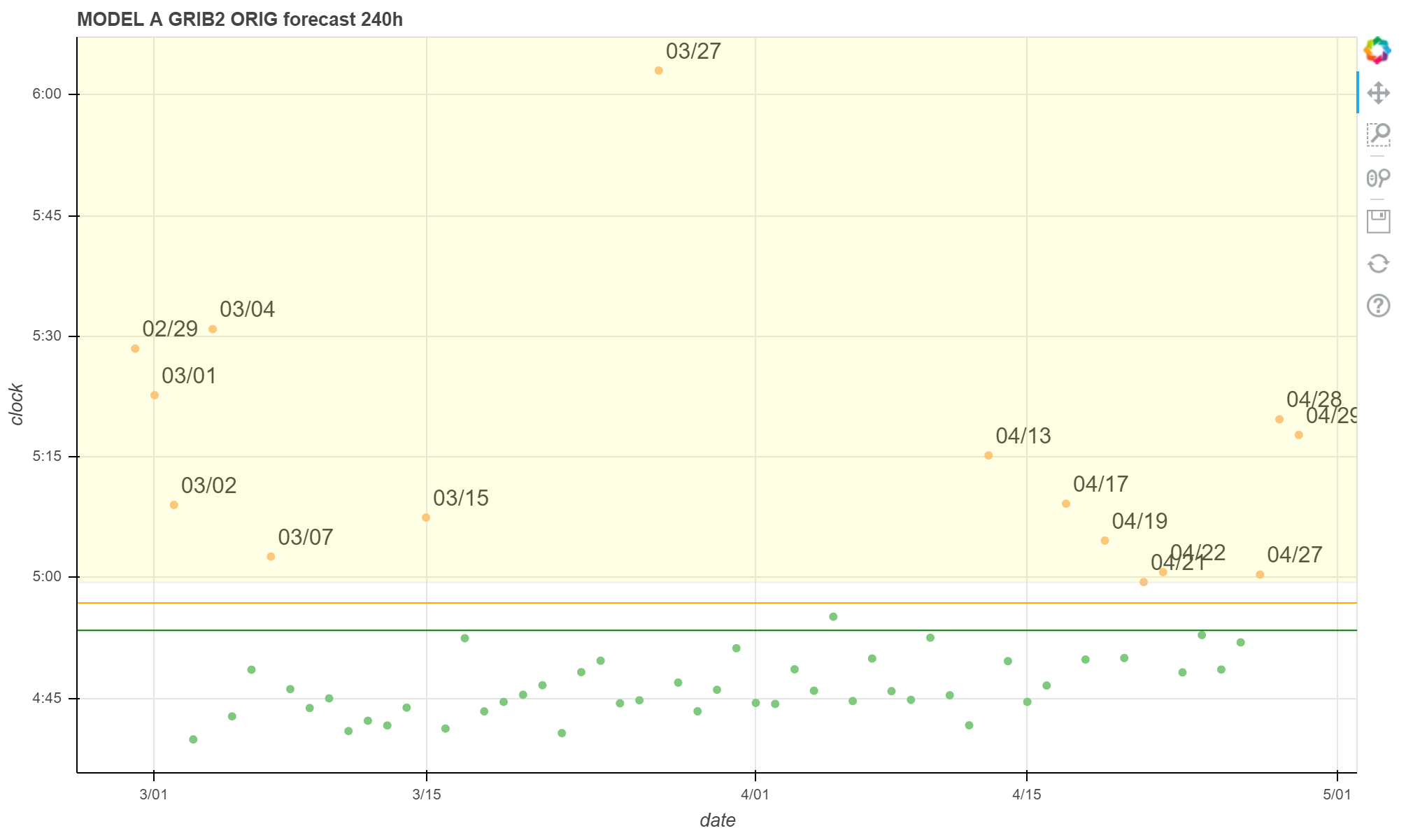
进一步分析
使用 Seaborn 绘制统计图形
直方图
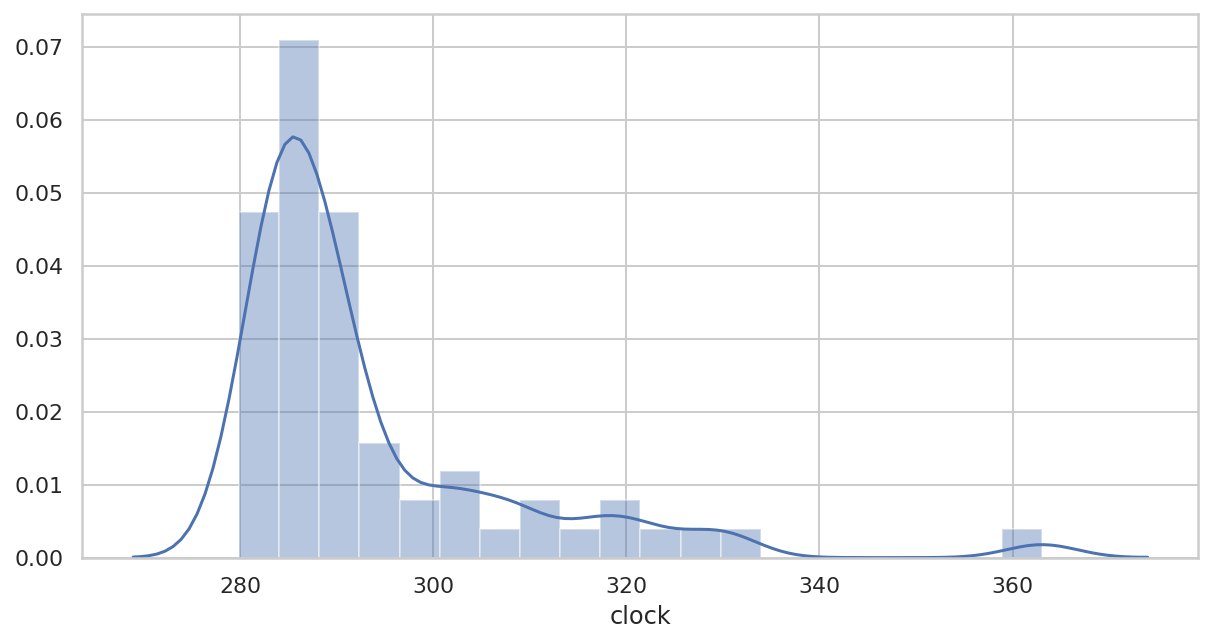
原始数据
plt.figure(figsize=(10, 5))
ax = sns.distplot(
df["clock"]/pd.Timedelta(minutes=1),
bins=20
)
重采样数据
plt.figure(figsize=(10, 5))
ax = sns.distplot(
bdf["clock"]/pd.Timedelta(minutes=1),
bins=20
)
ax.set_xlabel("clock [minutes from 00:00]")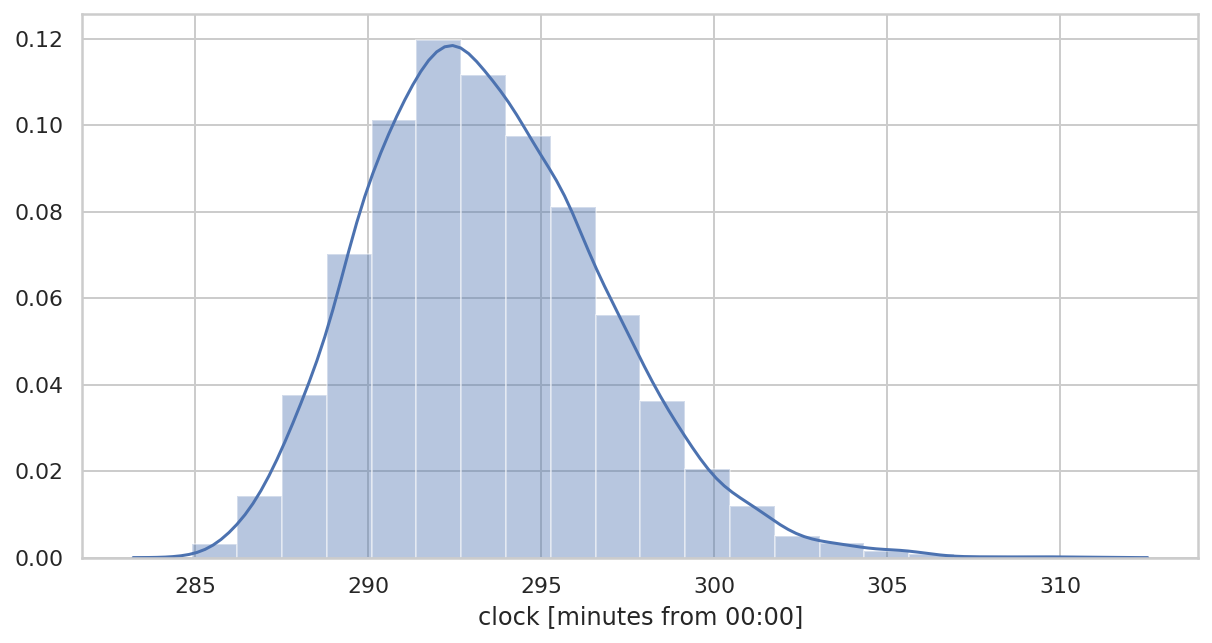
可以看到,重采样的数据更近似于正态分布。
箱线图
原始数据
f, ax = plt.subplots(figsize=(10, 5))
sns.boxplot(
x=df["clock"]/pd.Timedelta(minutes=1),
ax=ax
)
ax.set_xlabel("clock [minutes from 00:00]")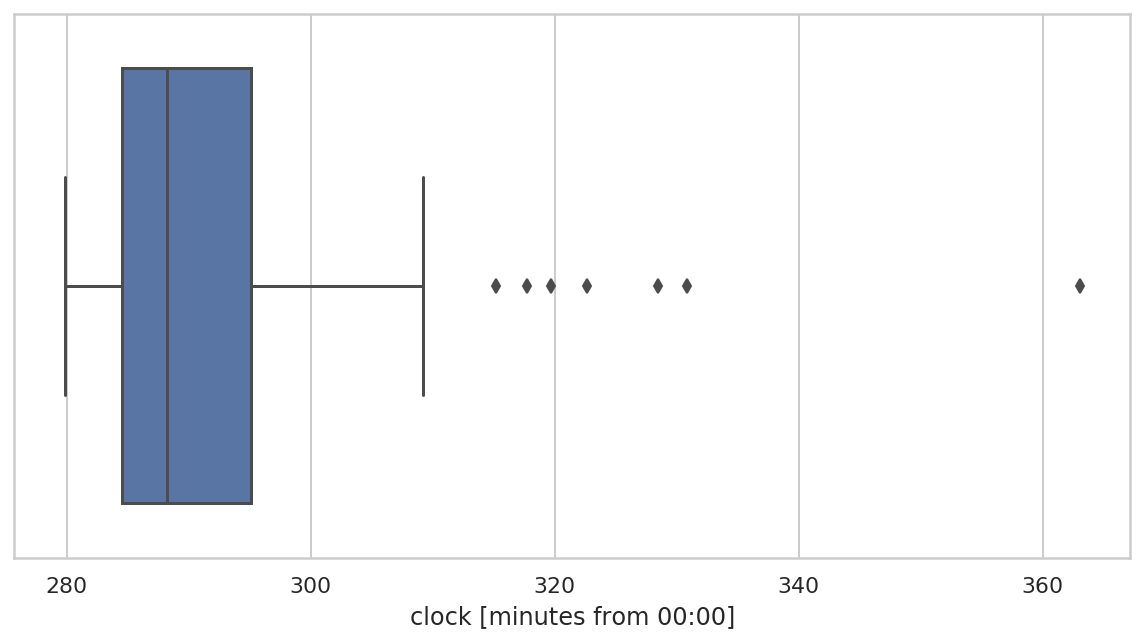
重采样数据
f, ax = plt.subplots(figsize=(10, 5))
sns.boxplot(
x=bdf["clock"]/pd.Timedelta(minutes=1),
ax=ax
)
ax.set_xlabel("clock [minutes from 00:00]")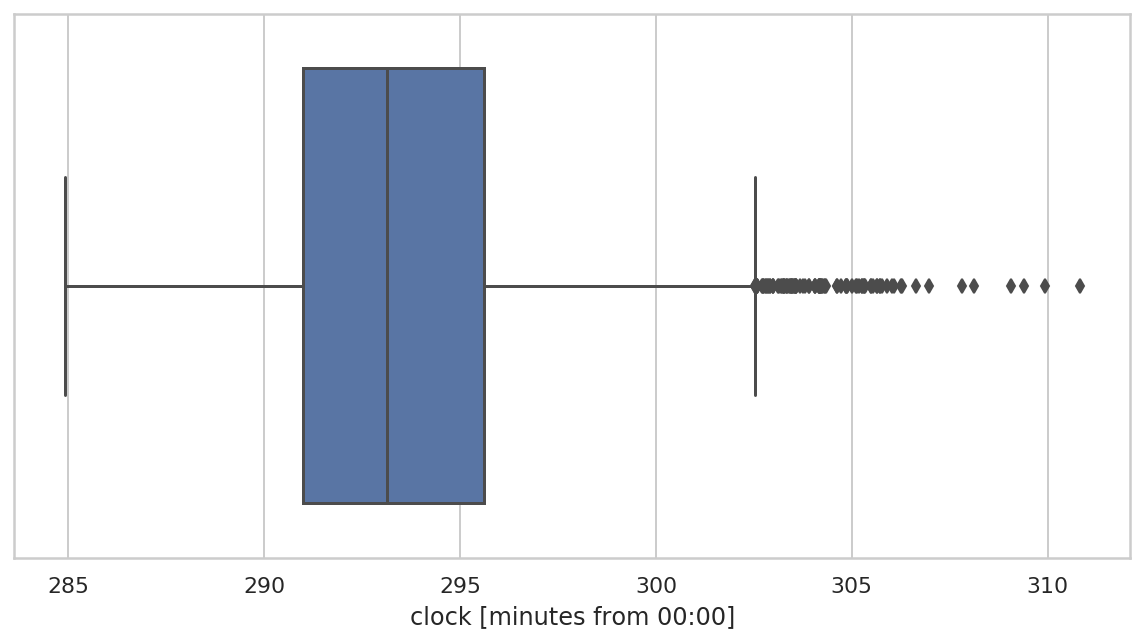
可以看到,重采样均值数据分布更集中。
虽然目前部门还没有明确的计算产品生成时间的方法,但笔者认为使用重采样方法计算的 95% 置信区间可以作为一个参考。
